Einstein旋转圆盘几何性质的研究

韩双明，白秀英

(渭南师范学院a.北校区教学部;b.物理与电气工程学院，陕西渭南714000)

2011年9月22日，意大利Gran Sasso Laboratory的“OPERA”项目研究人员公布了关于中微子超光速传播的最新结果［1］，该实验结果与Einstein相对论发生冲突，从而与上个世纪初建立起来的现代物理学的根基发生矛盾，引起物理学家以及科学界的普遍关注.大多数科学家之所以坚持光速是自然界的极限速度，是基于1905年Einstein在德国《物理年鉴》发表的Elektrodynamik bewegter K o¨rper［2］论文以及“光速不变”、“相对性原理”［3］的认可.简言之，如果有超光速运动质点存在，则Lorentz变换、长度收缩、时间延缓、质能关系等公式中的β≺0;更为重要的是，假如质点在惯性系中运动的速度大于光速，将会出现时间倒流，最终导致物理学因果律的破坏.从Einstein创立相对论以来，4维相对时空观已普遍为物理学家所接受，一切自然界质点运动速度不可能超过真空中光速已经成为不争的事实.本文试图以Einstein旋转圆盘的几何性质为研究，在狭义相对论时空结构中得到超光速“设想”的否定结论，研究旋转圆盘的几何性质，并给出非惯性系下“时空弯曲”的直观图景.

1 GR中Einstein旋转圆盘的周长

以等效原理和广义协变原理为基础，1916年，Einstein建立起广义相对论(以下简称GR)的理论大厦.Einstein选择黎曼几何作为数学工具，借助于一个思想实验——Einstein旋转圆盘，进一步揭示时间、空间的根本属性及其与物质分布、物质运动之间内在的深刻联系.在GR中，静止的实验室(K系)中安放的一个绕固定轴以角速度ω高速旋转的圆盘即Einstein旋转圆盘.若选取相对于这个圆盘静止的参考系为K'系，除原点外，在圆盘上距原点距离为r的每一点向心加速度都为ω2r，因此，对于K系中的观察者来说，K'系是非惯性系，而对于K'系中的观察者来说，他相对于圆盘静止，无论在哪里，都会受到一个向外的力即惯性离心力，即处在强度为ω2r的引力场中.在GR中，不同的参考系是通过物理度规来体现的，因此，只要给出时空度规张量 gμν(μ =0，1，2，3)，旋转圆盘问题即可解决［4］.对以 ω 匀速旋转的圆盘，若选取柱坐标表示空间的位置，并使z轴和z'轴与旋转轴重合，设静止系统的空间坐标为r'，φ'，z'，旋转系统的空间坐标为r，φ，z.则静止系统中的距离间隔为

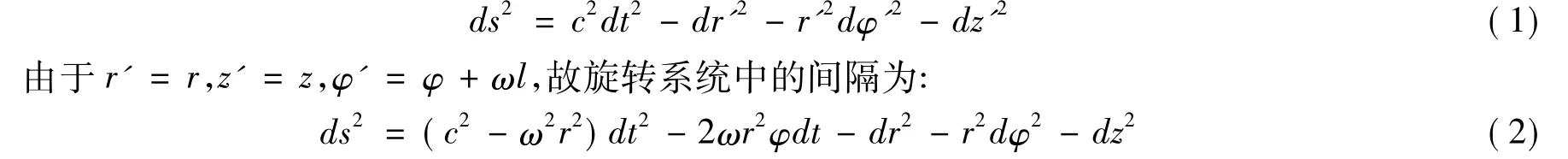
如若将 ct，r，φ，z用 xμ表示(μ =0，1，2，3)，并将其与通式比较可得到度规张量 gμν所有不等于0的度规为

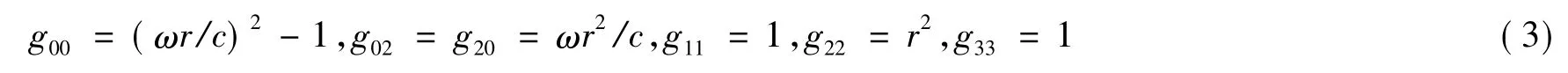
在非惯性系中，空间距离元的计算公式为

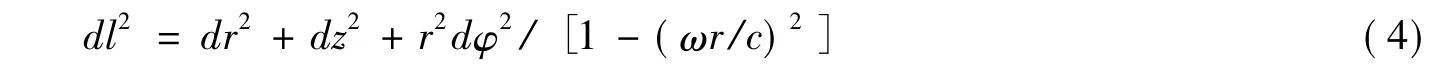
其中：i，k=1，2，3 时，xi和 xk分别对应 r，φ，z.现将(3) 中 gμν代入(4) 式得

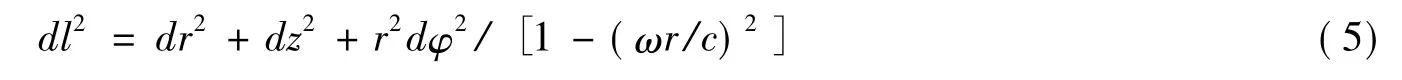
如果仅考虑垂直于z轴的圆弧，则dr=0，dz=0可得

2 SR中旋转圆盘的几何性质

若圆盘静止时半径为R，周长为L0=2πR.当圆盘绕过盘面垂直的对称轴以角速度ω旋转时，由于旋转盘上质点的运动速度与半径垂直，因此，圆盘的半径仍然为R.但是，由于Lorentz收缩，实验参考系中观察者测量的旋转圆盘周长必将小于2πR.因此，严格地说，圆盘上各个质点都作变速运动，从而使圆盘的形状发生了变化.若想得到实验室参考系与圆盘静止参考系间的变换规律，就已经超出了SR的研究范畴.但是，如若仅仅讨论旋转圆盘的周长L，则可以采用特殊方法绕开非惯性系问题(例如通过坐标系的选择)即可处理［5］.具体方法是：将圆盘进行无限细分，得到无数无限小的线段.然后以线段为研究对象分别建立实验坐标系，并使坐标原点位于圆心，坐标系的x轴与小线段平行，应用Lorentz变换得到各线段长度与其固有长度的关系，最后积分即可.

假设其中某一线段圆心角为dθ，固有长度为Rdθ，由Lorentz变换可得实验参考系中长度为：

(9)式中c为真空中的光速，ν为相对于实验坐标系下线段的速率.由于圆盘上各个质点运动速率ν相同，因此，将(9)式沿圆周积分可得

由(15)式可知，无论Einstein圆盘半径多大，当它以ω旋转时，周长不可能超过2πc/ω.将(15)式除以旋转周期T，可得

(16)式表明，无论Einstein旋转圆盘半径多大，旋转圆盘上各点的速度都不可能超过光速c.从而在SR中证明，一切质点运动的速度均不可能超过光在真空的运动速度.

3 SR中旋转圆盘的几何形状

在非惯性系中，由于时空是弯曲的，对于圆盘来说，当它绕垂直于圆面的对称轴旋转时，圆盘周长与半径R不是正比关系，惯性系中的平面在非惯性系中将变成曲面，该曲面弯曲程度由非惯性参考系决定.

对于以匀角速ω随着圆盘旋转的非惯性系来说，其空间曲率半径为ρ=c/ω，从而在惯性系下，无限大平面变为半径R等于c/ω的半球面(如图1所示).同样地，静止半径为R的圆盘面将变为一球冠，其空间曲率半径为c/ω，球冠的边缘周长与半径为L=2πr.也就是说，以角速度ω旋转的静止半径为R的盘面为一球冠，其边缘半径为

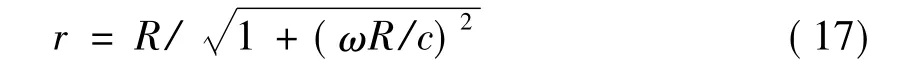
图1中，如果从z轴中心向球冠边缘一点任意作射线，射线与平面交点对应的半径即为静止半径R，如图2所示，由几何关系知

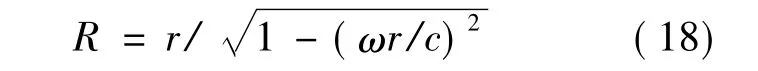
(18)式是由SR时空观得到的旋转圆盘半径，该结果与GR中得到的圆盘半径(8)式完全吻合.

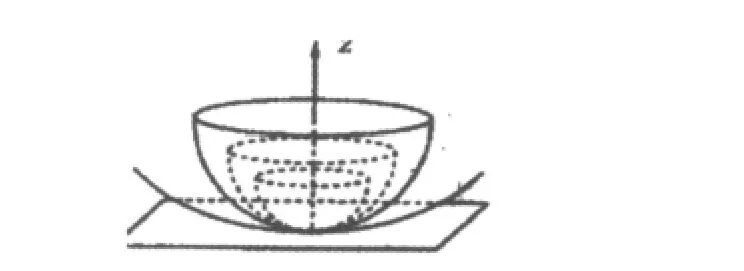
图1 无限大平面成为无限大的半球面

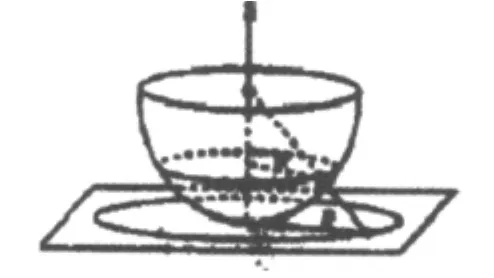
图2 半径为R的球冠

4 结论

通过以上SR时空观中旋转圆盘几何性质的研究，可以得到：

(1)Einstein旋转圆盘周长的上限为2πc/ω，盘上质点运动速率的上限为c，在狭义相对论效应内，旋转圆盘上质点运动的超光速不会出现.

(2)旋转圆盘由于时空弯曲，其几何形状为球冠，球冠半径为R/

(3)Einstein旋转圆盘的几何形状及空间距离，在GR与SR下所得结论一致，表明旋转圆盘问题在SR范围亦可解决.

［1］Adam T，Agafonova N，Alekssandrov A，et al.Measurement of the neutrino velocity with the OPERA detector in the CNGSbeam［DB/OL］.(2011 －09 －22)［2012 －09 －26］.http：//fr.arxiv.org/abs/1109.4897.

［2］Einstein A.论动体的电动力学［M］//范岱年，赵中立，许良英，译.爱因斯坦文集：第2卷.北京：商务印书馆，1983.83－115.

［3］Einstein A.关于相对性原理和由此得出的结论［M］//.范岱年，赵中立，许良英，译.爱因斯坦文集：第2卷.北京：商务印书馆，1983.150 －210.

［4］［俄］朗道，EM 栗弗席兹.场论［M］.任朗，袁炳南，译.北京：人民教育出版社，1959.311.

［5］姜孟瑞，张磊.相对论中旋转圆盘的几何性质［J］.山东师范大学学报(自然科学版)，2005，20(4)：109－111.