基于变分法的一元非线性回归分析

张同琦，李 凤

(渭南师范学院数学与信息科学学院，陕西渭南714000)

通常所谓的一元非线性回归问题，都是假定两个随机变量ξ，η之间的非线性函数关系是已知的，例如η =aebξ，给定(ξ，η) 一组样本值(xi，yi)(i=1，2，…，n) ，要求对其中的参数a，b作出估计，解决的方法是用变量代换，将其化为线性模型［1－5］.例如，令 Y=lnη，则有Y=ln a+bξ，这种情形，本质上仍是线性回归问题.本文研究具有统计相关关系的二维连续型随机变量(ξ，η)的非线性回归分析问题：η=f(ξ)+ε，ξ的分布是已知的，ξ与ε独立，ε ～N(0，σ2)，要求从给定的一组样本值(xi，yi)(i=1，2，…，n)来确定未知函数f(x).首先得出(ξ，η)的联合密度函数为.其次研究φ(x，y)的统计学性质和几何性质，由条件密度的表达式，易知，在过点(x，0)且平行于y轴的直线上，点(x，f(x))处的密度函数达到最大值，从而得到在xoy平面上的一切有二阶连续导数的曲线g(x)中，对给定的点＞ φ(x，g(x))，即曲线y=f(x) 是00一条极值曲线，从而将非线性回归问题归结为泛函极值问题，应用变分法，求出未知函数的分析表达式.本文对所提问题的研究有一定方法论方面的意义.

1 一元非线性回归模型及其性质

已知连续型随机变量ξ的密度函数为φξ(x)，另一随机变量η=f(ξ)+ε，ξ的分布是已知的，ξ与ε独立，ε ～ N(0，σ2).f(x) 为有二阶连续导数的未知函数，要求由给定(ξ，η) 的一组样本值(xi，yi)(i=1，2，…，n)来确定未知函数f(x).

首先，我们有如下定理：

定理1 设φξ(x)是连续型随机变量ξ的密度函数，令η =f(ξ)+ε，则二维随机变量(ξ，η)的联合密度为

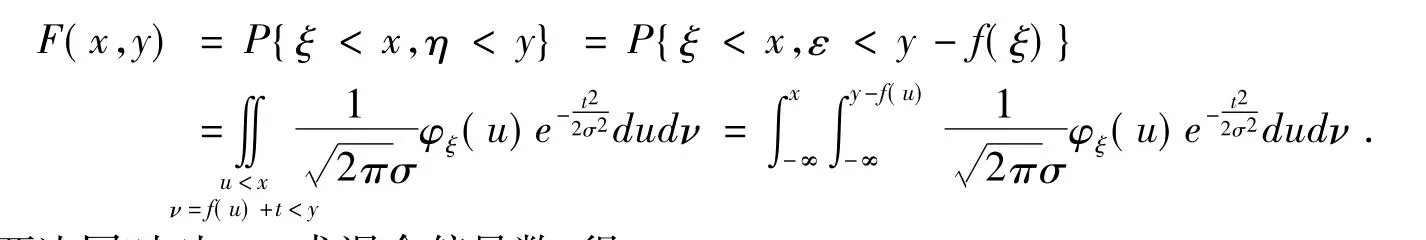
上式等号两边同时对x，y求混合偏导数，得

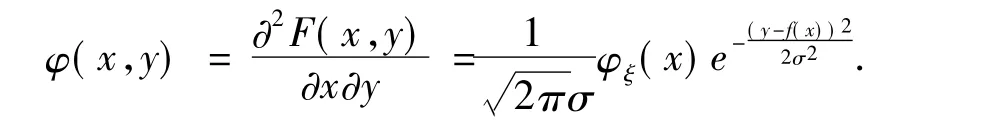
显然，φ(x，y)有以下性质：

以上结果表明：当ξ=x时，条件分布φη|ξ(y|x)是以f(x)为中心的正态分布，条件密度曲线是过点(x，0)且垂直于x轴的平面与曲面φ(x，y)的截线(如图1).

研究xoy平面上过点(x，0)且平行于y轴的直线l上各点处的条件密度性质，易知，在点(x，f(x))处密度函数达到最大值，同理xoy平面上过另一点(x，0)且平行于y轴的直线l上点(x，f(x))111处密度函数达到最大值，这些点(x，f(x))、(x1f(x1))所在的曲线正好是曲线y=f(x).这说明，曲线y=f(x)上的总质量ds比任一条平面曲线y=g(x)的总质量都大，称曲线y=f(x)为极值曲线.

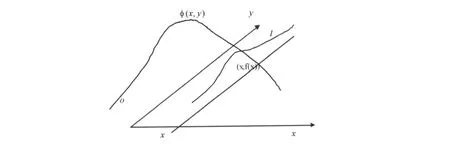
图1

2 用变分法求极值曲线y=f(x)

根据以上分析，本文研究的非线性模型中的未知函数y=f(x)是xoy平面上的一条极值曲线y=g(x)，(ξ，η) 的联合密度为 φ(x，y)，在其上的总质量达到最大值.换言之，在一切有二阶连续导数的平面曲线y=g(x)中，只有一条曲线使ds达到最大值.到此本文研究的一元非线性回归问题，归结为泛函极值问题.

为求本文中的非线性模型中的未知函数y=f(x)，可分为三种情形：

(1) 给定(ξ，η) 的一组样本值(xi，yi)(i=1，2，…，n)，求y=f(x) 使到最大;

(2) 给定(ξ，η) 的一组样本值(xi，yi)(i=1，2，…，n)，求 y=f(x)，在约束条件 E(η) =＜ + ∞ 下，使达到最大;

(3)对y=f(x)附加条件，将附加条件作为约束条件，使达到最大.

下面分别对(1)、(2)两种情形，求未知函数y=f(x)：

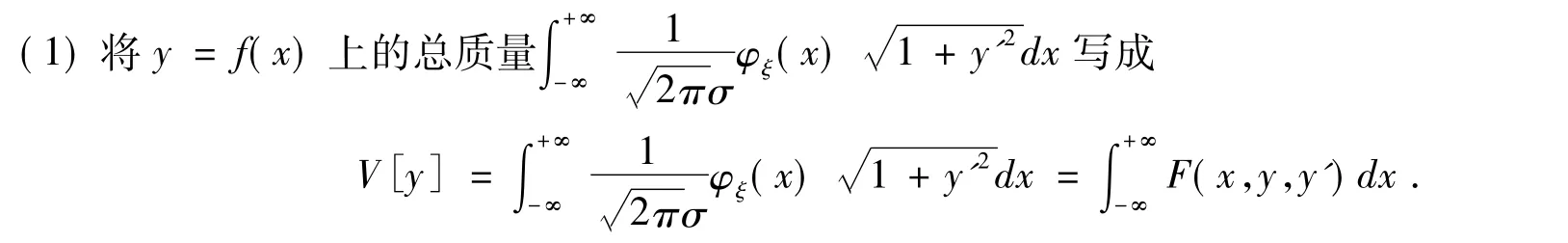
上式是以y=f(x)为未知函数的泛函极值问题，且F只依赖x和y'，由变分法［1］，相应的尤拉方程为=0，即，或

这是一个二阶非线性微分方程，积分后得出未知函数的一般形式

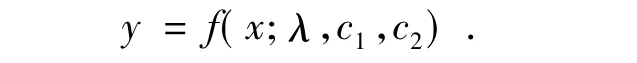
其中c1，c2是两次积分常数.给定的一组样本值(xi，yi)(i=1，2，…，n)，令W(λ，c1，c2)= ∑(yi－ f(xi;λ，c1，c2))2，应用最小二乘法，得方程组

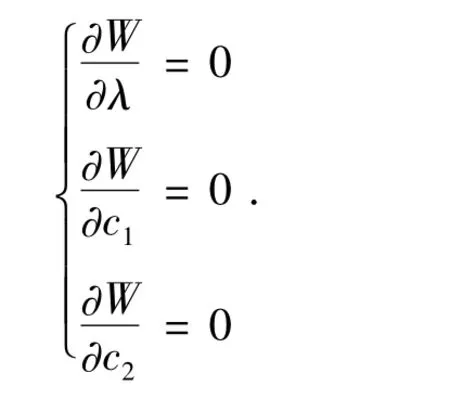
解方程组，得出 λ、c1、c2的估计值，从而得到 y=f(x) 的回归表达式

3 应用算例

(1)第一种情形

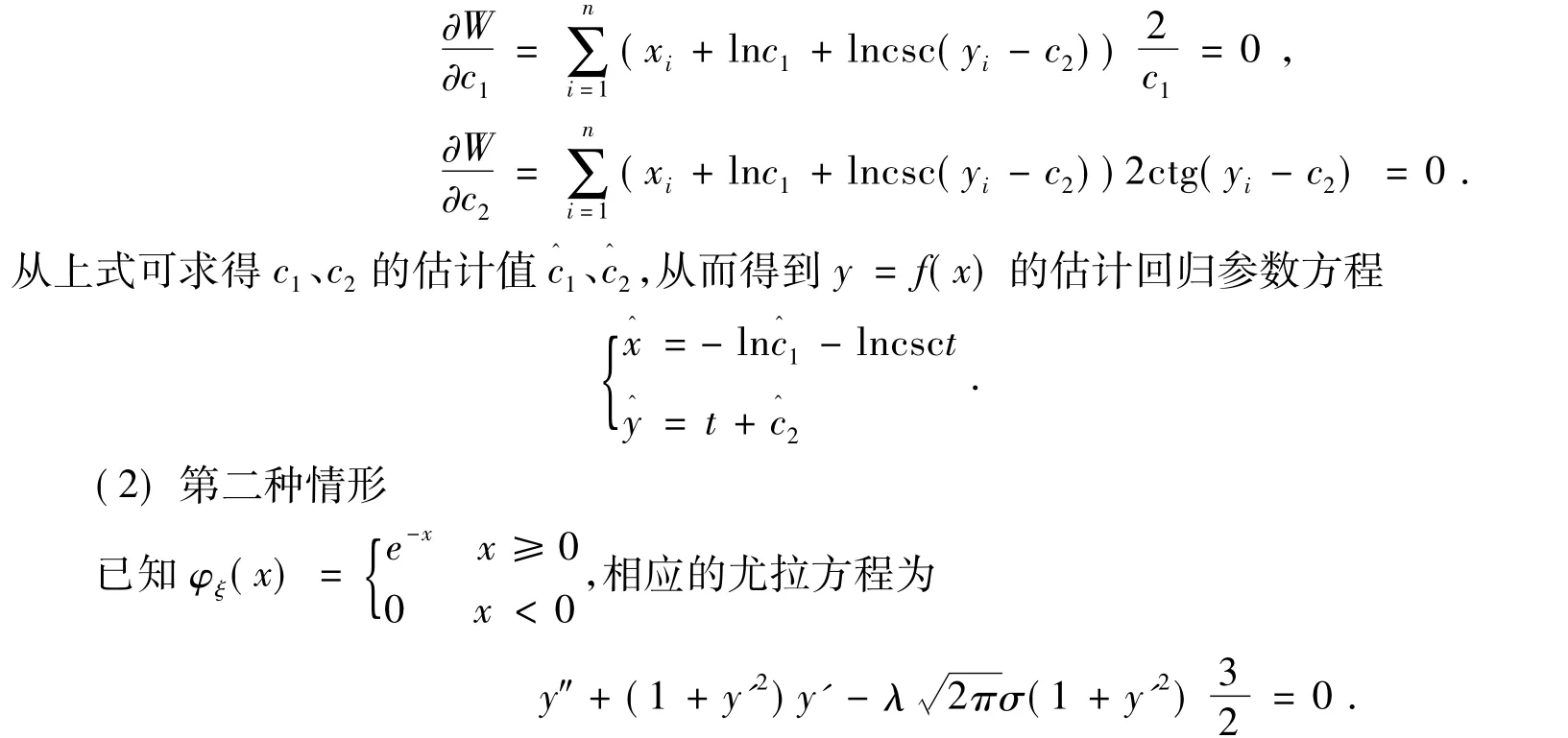
引入参数t，使y'=tgt，则尤拉方程呈如下形式

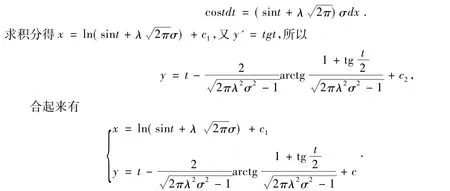
给定的一组样本值(xi，yi)(i=1，2，…，n)，应用最小二乘法，得出 λ、c1、c2的估计值，从而得到y=f(x)的估计回归参数表达式

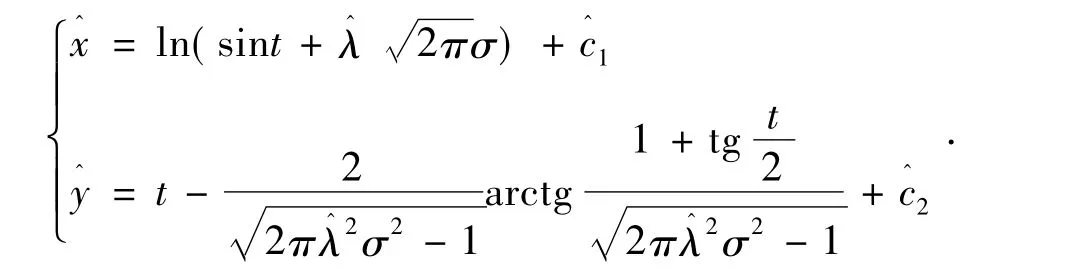
［1］［美］Douglas M.Baces，［加拿大］Donald G.Watts.非线性回归分析及应用［M］.北京：中国统计出版社，1997.

［2］书博成.非线性回归分析［M］.南京：东南大学出版社，1998.

［3］［苏］艾利斯哥尔兹.变分法［M］.北京：人民教育出版社，1958.

［4］CHEN Jin-hong.Gemai Semi parametric generalized least squares estimation in partially linear models with correlated errors［J］.Journal of statistical planning and inference，2007，137：117 －132.

［5］Huang J.Z，Shen H.P.Functional coefficient regression models for nonlinear time series：A polynomial spine approach［J］.Scandinavian Journal of Statistics，2004，31：515 －534.