混合分数布朗运动下可延迟交付的附息债券期权定价

张 璐，容跃堂，刘明月

(西安工程大学理学院，西安710048)

0 引言

由于金融市场中股票价格具有长期依赖性和自相似性，近年有部分学者［1-4］使用混合布朗运动来研究欧式期权.使用混合分数布朗运动(α，β)=+βWt，t≥0作为来驱动金融市场，这种噪声与半鞅有着相类似的性质，且在Hurst指数H≥3/4时，这个随机过程即等价于一个常数乘以Brownian运动.当H∈(1/2，1)时，混合分数布朗运动所驱动的市场是完备的且无套利.因此，本文采用混合分数布朗运动的ItÔ公式［5］，获得了混合分数布朗运动过程下的可延迟交付的附息债券期权定价模型，并选取了模型所满足的随机微分方程，最后证明了欧式延迟交付的附息债券看涨期权定价公式.

1 基本假设

现考虑这样一个混合型Black-Scholes市场即有混合分数布朗运动α，β)=+ βWt，t≥0 驱动的市场.原生资产价格演化遵循混合分数布朗运动.其中标的资产的价格S(t)满足

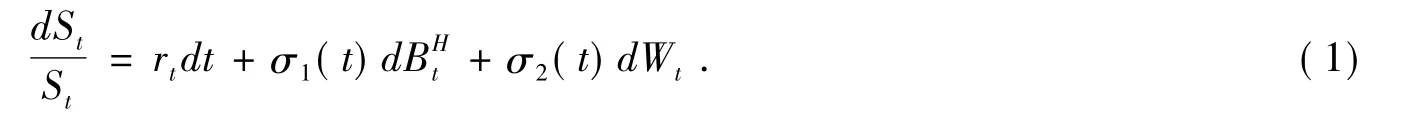
其中：rt为短期利率;σ1(t)，σ2(t)为波动率(关于t的确定性函数);dBH(t)为分数布朗运动;dW(t)为布朗运动.

市场中的基本变量过程是服从Hull—White模型的短期利率过程

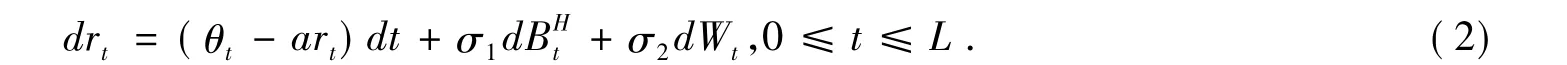
其中：θt是时间t的确定性连续函数，且a，σ1，σ2均为正常数 .

市场中的所有衍生证券Y的价格过程为Y(t，rt，TY)，其中TY≤L，［0，TY］是衍生证券Y的有效期，且函数Y(t，rt;TY)∈C1(［0，TY］)×(-∞，+∞)).假设不支付交易费和税收，且市场是完全的，不存在套利机会.

2 零息票债券定价公式

引理1 在以上基本假设下，市场中的衍生证券Y的价格函数Y(t，rt;TY)适合以下偏微分方程：

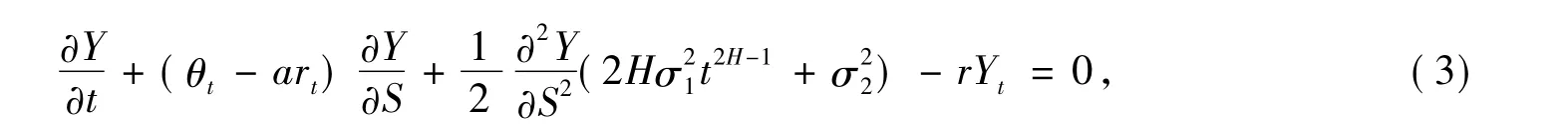
其中(t，r) ∈［0，TY］× (- ∞ ，+ ∞).

证明 现考虑一个投资组合∏ =Yt-△St，有

设Y=Y(St，t)是一个二元可微函数，若随机过程St适合随机微分方程dSt=μdt++ σ2dWt，则

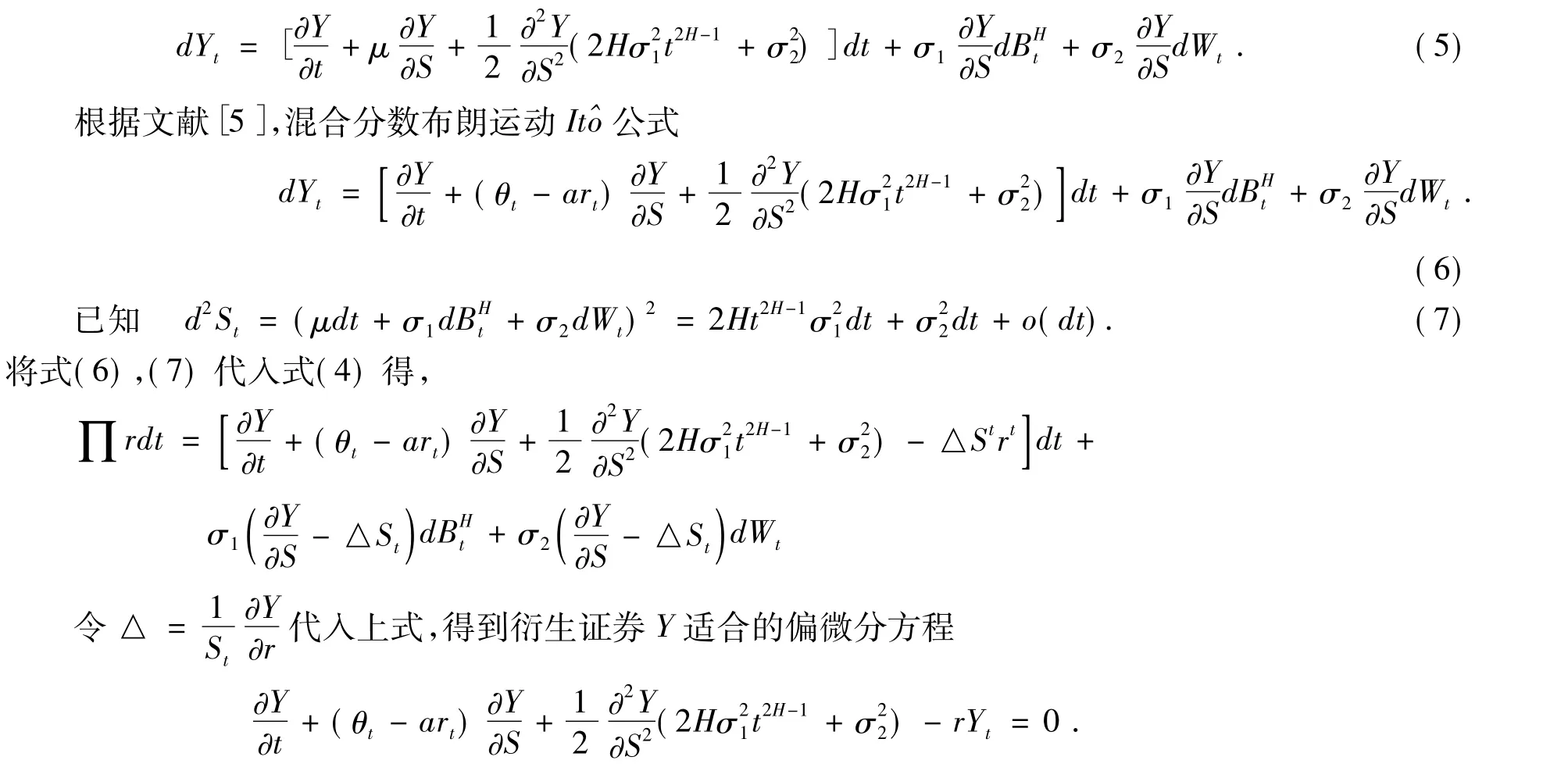
引理2 在基本假设下，令P(t，r，T)表示零息票债券在t时刻的价格，到期日为T，那么混合分数布朗运动下零息票债券P(t，r，T)的定价公式为

证明再根据零息票债券价格函数在到期日P(t=T，r;T)=1的特征可得到(9)成立.P(t，r;T)满足式(3)，利用伊滕引理及偏微分方程方法可证明(8)成立.

3 模型建立与求解

根据文献［6］，考虑标的资产为附息票债券P的欧式看涨期权，其执行价格为K，到期日为T，附息票债券的交付日期T˜.期权的价格函数表示为Y(t，r;T，T˜).本文研究可延期交付的附息票债券期权标的资产的交付日期T˜与期权到期日T不一定相同，即T≤T˜≤T.因此，可将此期权分为三类：

(2)设tm＜T＜T-＜tm+1，即期权到期日与延迟交付日在同一个相邻息票交付日之间.因此需要将T-时刻可能要支付的执行价格贴现到T时刻与标的资产在T时刻的价值作比较.期权在T时刻的损益为Y(T，rT;T，=max{0，CiP(T，rT;ti)-KP(T，rT;}，此类可延期交付的附息票债券期权定价模型为

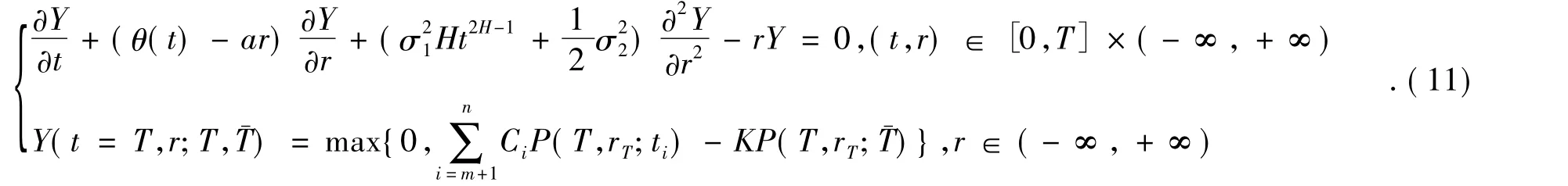
(3)设tm＜T＜tm+1＜… ＜tm+h＜＜tm+h+1＜… ＜tn=，即期权到期日与延迟交付日不在同一个相邻息票交付日之间.在期权到期日T和延迟交付日期 之间有附息票债券 有h次息票支付金额为Cm+1，…，Cm+h.期权持有人若执行期权，在延迟交付日期只能得到tm+h+1之后(包括tm+h+1)的所有息票和债券的面值，因此，该期权在到期日T时刻的损益为

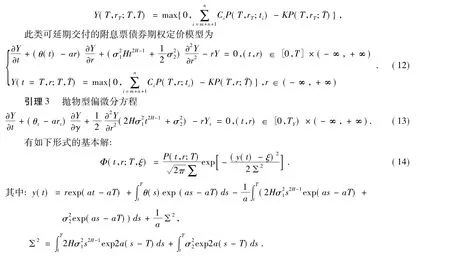
证明 偏微分方程(13)的基本解Φ(T-t，r-ξ)也是

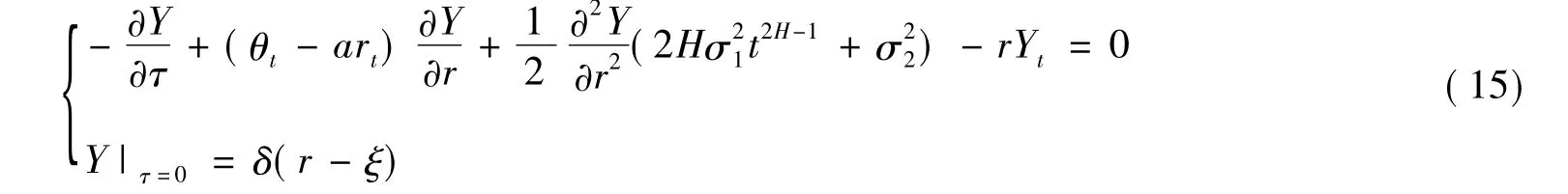
的解，其中δ(x)为Dirac函数.

设 Y(τ，r)= νexp(A(τ)-rB(τ))，由此得：

代入式(15)的微分方程后，有

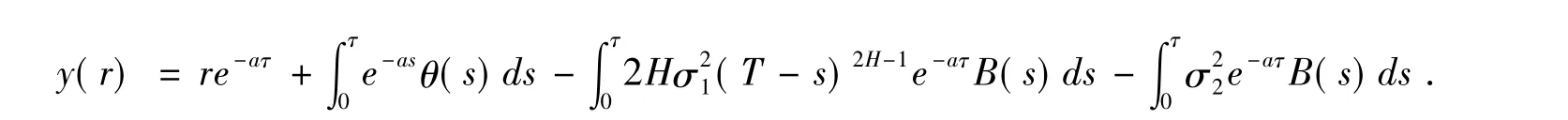
综上所述，引理中(13)微分方程的基本解的形式可表示为：

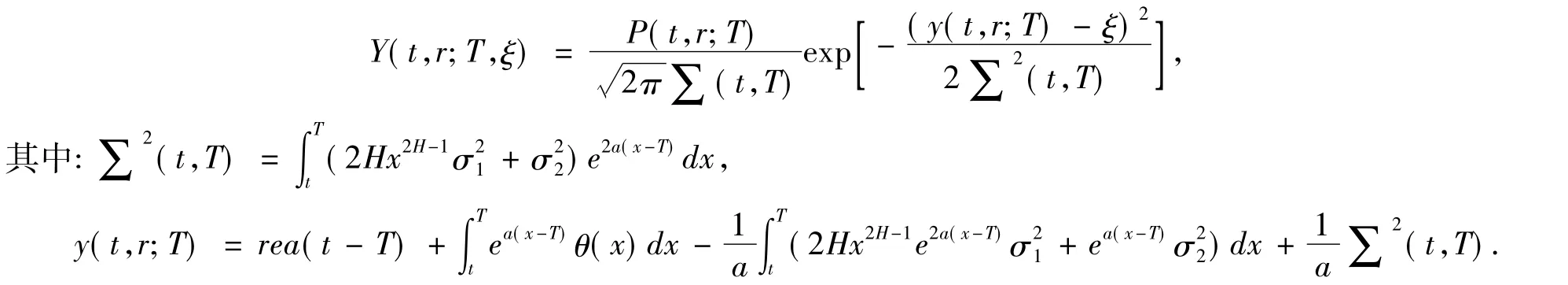
定理在基本假设下，模型(11)的解有如下表达形式：

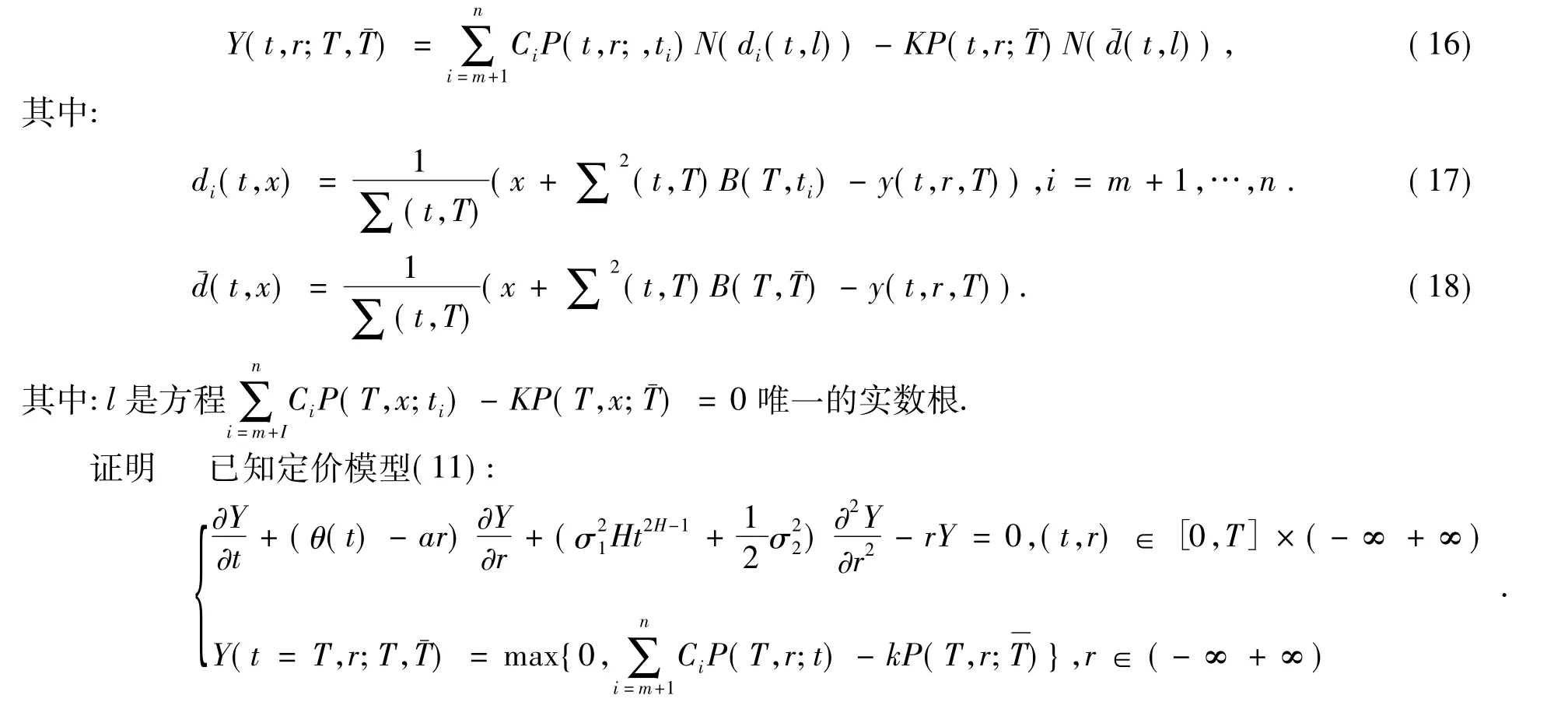
根据引理3可知，定价模型的解为

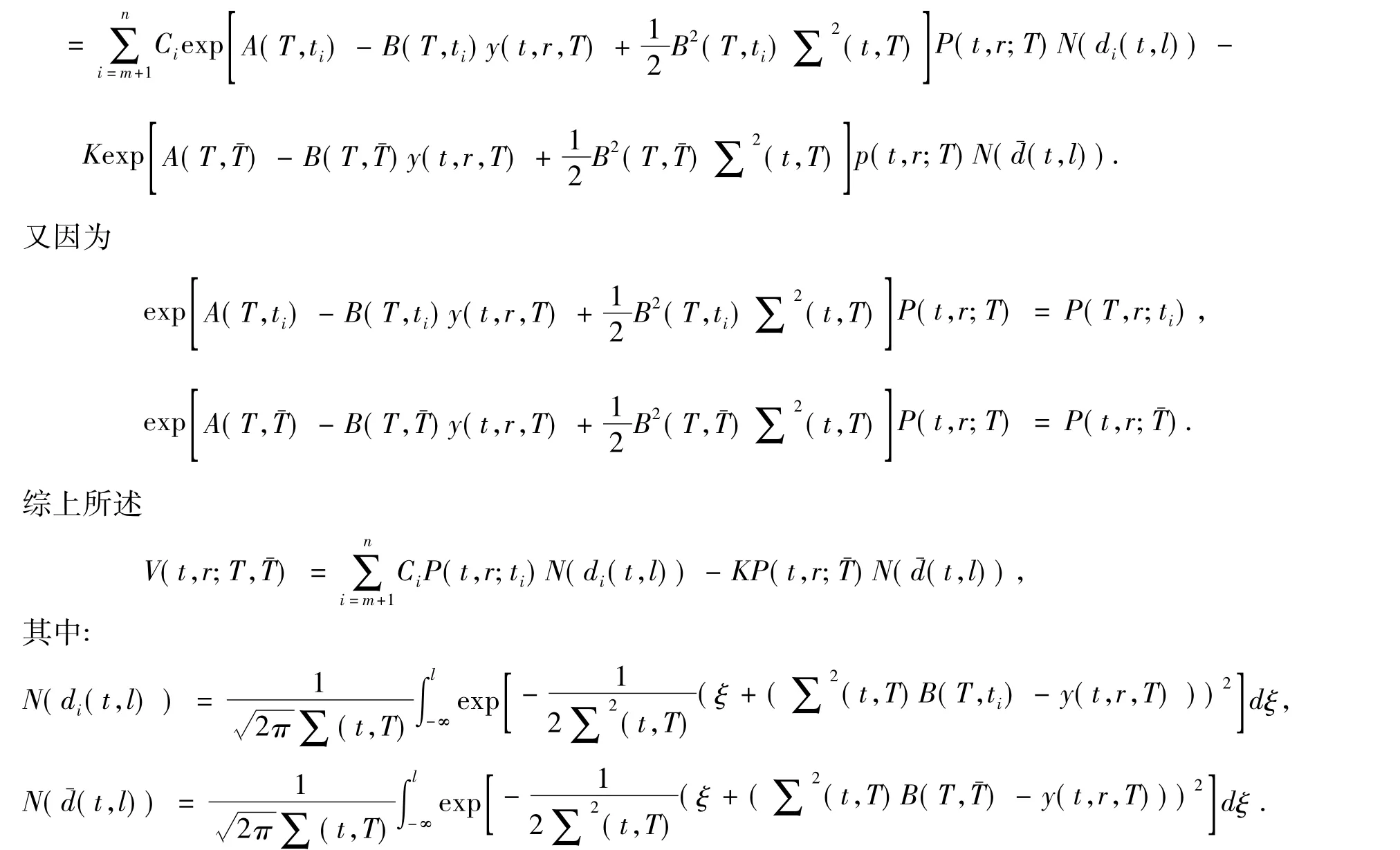
同理，可以得到此期权的另外两种类型的定价模型的解的表达式：

(2)若期权到期日与标的资产交付日相同，即为标准的欧式附息票债券看期权，其定价模型(10)的解为 V(t，r;T)=-KP(t，r;T)N()，其中：

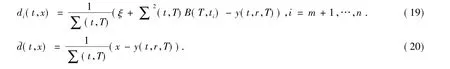
上述的 P(t，r;T)，B(t，T) 由引理2 给出l是方程(T，x;ti)-K=0唯一的实数根.N(x)为标准正态分布累积函数.经过验证可得，当=T时，(16)的解恰为表达式(10)的解.

推论 (欧式可延期交付的附息票债券看跌期权定价公式)Vp表示看跌期权，则

(III)设tm＜T＜tm+1＜… ＜tm+h＜＜tm+h+1＜… ＜tn=，即期权到期日与延迟交付日不在同一个相邻息票交付日之间.

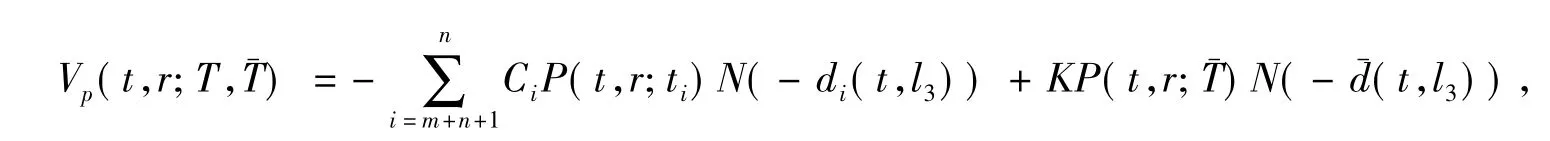
证明 利用期权看涨—看跌平价公式即可.

4 结语

文章结合了混合分数布朗运动随机分析理论以及偏微分方程方法对可延期交付的附息票债券期权价格进行定价，本文还有进一步的研究空间.

［1］Cheridito P.Regularizing Fractional Brownian Motion with a View towards Stock Pric Modelling［D］.Zurich ：Swiss Federal Institute of Technology Zurich，2001.

［2］Bender C，Sottine T，Valkeila E.Arbitrage with fractional Brownian motion［J］.Theory of Stochastic Processes，2006，12(3) ：1－ 12.

［3］Bender C，Sottine T，Valkeila E.Pricing by hedging and absence of regular arbitrage beyond semi martingales［J］.Finance and Stochastics，2008，12(4)：441－ 468.

［4］余征，闫理坦.混合分数布朗运动环境下的欧式期权定价［J］.苏州科技学院学报(自然科学版)，2008，25(4)：4－10.

［5］杨朝强.混合分数布朗运动下一类欧式回望期权定价［J］.山东大学学报(理学版)，2012，47(9)：105－109.

［6］RONG Yue-tang，ZHANGLu.The Pricing Formula for Coupon-Bonds Option with Delay in Delivery in Fractional Brownian Motion Environment［C］//2012 3rd International Conference on E-Business and E-Government.Shanghai：the IEEE Inc，2012.2256－2260.