弱诱导的L-fuzzy双拓扑空间中新的紧性

孙军娜，徐小玲，马保国

(1渭南师范学院数学与信息科学学院，陕西渭南714000;2延安大学西安创新学院，西安710100)

自从1963年J.C.Kelly［1］引入双拓扑空间的概念以来，国内外许多拓扑学者对其进行了一系列的研究［2－5］，使得双拓扑空间构成了拓扑学的一个研究分支.仿照分明拓扑学，郑崇友［5］等首次借助 α-δ1δ2远域族，将S-紧性、B-紧性引入到L-fuzzy双拓扑空间.1995年，孟广武［6］以强α－局部有限族为基础，在L-fuzzy拓扑空间中引入层仿紧性.此后，文献［7-8］基于几乎α-远域族，先后给出可数层仿紧集、几乎可数层仿紧集的定义，研究后得到了若干结果.本文在现有的理论基础上，将几乎可数层仿紧集引入到L-fuzzy双拓扑空间中，对其相关性质进行了讨论，得出了许多结论.

本文中，L=(L，≤，∨，∧，')表示fuzzy格，L的最大元是1，最小元是0且1≠0.M(L)与M*(LX)分别表示L与LX的非零分子之集，P(L)表示L的非1元素之集.X是非空分明集，对A⊂X，χA表示A的特征函数.LX表示X上的全体L-fuzzy集，其最大元与最小元分别是1X与0X.(LX，δ1，δ2)表示L-fuzzy双拓扑空间，η(xα)与η－(xα)分别表示xα的远域族和闭远域族.对A∈LX及α∈M(L)，Ω⊂δ'1∪δ'2称为A 的 α-δ1δ2远域族(α-δ1δ2RF)，若 ∀xα∈ A，∃Q ∈ Ω，使 Q ∈ η－(xα);对 A ∈ LX，α ∈ M(L)，R ⊂ LX，令 Aqα=∨{xα∈ M*(LX)|xα≮ A}，Rqα={Aqα|A ∈ R} .τα(A)={x∈ X|A(x) ≥ α}，lα'(A)=x∈X|A(x)α'}.对分明双拓扑空间(X，τ1，τ2)，以R表示其任一可数开覆盖，N(x)表示x的开邻域系，φ表示分明空集.若A∈LX，则Ao，A－，A'分别表示L-fuzzy集A的内部、闭包和伪补.其他未说明的概念与符号均见文献［9］.

1 预备知识

定义 1［5］设 δ1，δ2都是 LX上的 L-fuzzy 拓扑，则(LX，δ1，δ2) 称为 L-fuzzy 双拓扑空间.

定义2［6］设(LX，δ) 是 L-fuzzy拓扑空间，A ∈ LX，α ∈ M(L)，称 Ω ={Bt∶t∈ T}⊂ LX在 A 中强α-局部有限，若∀xα∈A，存在分明集P使χp∈η(xα)且存在有限子集T0⊂T使∀t∈T－T0，Bt≤χp.当A=1X时，简称Ω是强α-局部有限族.

引理1［8］设 f∶(LX1，δ1) → (LX2，δ2) 是连续的 L-zadeh 型函数，A ∈ LX2，α ∈ M(L).若 △ ⊂ LX2在A 中强 α-局部有限，则 f－1(△)={f－1(B)|B ∈ △} 在 f－1中强 α-局部有限.

定义3 设δ1，δ2都是非空集X上的L-fuzzy拓扑，A∈LX，α∈M(L)与Ω⊂2δ1'∪δ2'.若对于A中高为 α的任意分子xα(即xα∈M(LX)，xα≤A)，存在P∈Ω 使得xαPo，则称 Ω 是A的几乎 α-δ1δ2远域族.

易知，A 的 α-δ1δ2远域族［4］必是 A 的几乎 α-δ1δ2远域族.

2 几乎可数层仿紧集的定义及刻画

定义4 设(LX，δ1，δ2) 是 L-fuzzy双拓扑空间，A ∈ LX，α ∈ M(L)，称 A 是几乎可数层 α-δ1δ2仿紧的，若对A的任一可数α-δ1δ2远域族Ω，存在Ω余加细的有限子族Ψ，使得

(ⅰ)Ψ 是 A 的几乎 α-δ1δ2远域族;

(ⅱ)Ψ'∧A={D'∧A|D∈Ψ}在A中强α-局部有限.

若对∀α∈M(L)，A都是几乎可数层α-δ1δ2仿紧的，则称A是几乎可数层仿紧的.如果A=1X是几乎可数层 α-δ1δ2仿紧的(几乎可数层仿紧的)，则称空间(LX，δ) 是几乎可数层 α-δ1δ2仿紧的(几乎可数层仿紧的).

定理1 设(LX，δ1，δ2) 是 L-fuzzy双拓扑空间，B ∈ δ'1∪ δ'2，α ∈ M(L).

(ⅰ)如果A∈LX是几乎可数层α-δ1δ2仿紧的，则A∧B是几乎可数层α-δ1δ2仿紧的.

(ⅱ)如果A∈LX是几乎可数层仿紧的，则A∧B是几乎可数层仿紧的.

证明 只需证明(ⅰ).

设 α∈M(L)且Φ是A∧B的可数α-δ1δ2远域族.令Ω =Φ∪{B}，则Ω是A的可数α-δ1δ2远域族，由A是几乎可数层α-δ1δ2仿紧集知有余加细Ω的A的几乎α-δ1δ2远域族Ψ使得Ψ'∧A在A中强α-局部有限.

令S={D∈Ψ|D⊄B}，则S是A∧B的几乎α-δ1δ2远域族且是Φ的余加细.显然，S'∧B∧A在A中强α-局部有限，从而S'∧B∧A在A∧B中强α-局部有限.因此A∧B是几乎可数层α-δ1δ2仿紧的.

推论1 L-fuzzy双拓扑空间中的几乎可数层仿紧集对闭子集遗传.

定理2 L-fuzzy双拓扑空间中的几乎可数层仿紧集对闭子空间遗传.

定义5［8］称集族{x}，x∈ X，是 X 的近似子覆盖，若是X的覆盖，即ii∈N

定义6 一个分明双拓扑空间X是几乎可数仿紧的当且仅当X的每一个可数开覆盖都有一个局部有限的子集族，它的闭包覆盖X，等价于：每一个可数开覆盖都有一个局部有限的近似子覆盖是它的加细.

定理3 设(LX－，δ1，δ2)是弱诱导L-fuzzy的双拓扑空间，则下列条件等价：

(ⅰ)(LX－，δ1，δ2) 是几乎可数层仿紧空间.

(ⅱ)∃α ∈ M(L)，使得(LX－，δ1，δ2) 是几乎可数层 α-δ1δ2仿紧空间 .

(ⅲ)(LX－，δ1，δ2) 的底空间(X，［δ1］，［δ2］) 是几乎可数仿紧空间 .

证明 (ⅰ)⇒(ⅱ)显然 .

(ⅱ)⇒(ⅲ) 设 R是(X，［δ1］，［δ2］) 的任一可数开覆盖，则χR'={χD'|D∈R} ⊂δ'是1X的可数α-δ1δ2远域族.于是存在1X的几乎 α-δ1δ2远域族 Ψ ={Pt|t∈T}，使得 Ψ 是 χR'的余加细，且 Ψ'在1X中强 α-局部有限.令 Φ ={lα'(Pt')|(t∈ T}，则 Φ 是(X，［δ1］，［δ2］) 的近似开覆盖.∀t∈ T，∃D ∈ R，使 χD'≤ Pt，从而 χD≥⊂lα'(χD)={x∈ X|χD(x) α'}={x∈ X|χD(x)=1} ⊂ D，则 Φ是R的加细.∀x∈X，有xα∈1X，从而存在分明闭集W使χW∈η(xα)，且存在T0⊂T使∀t∈T－T0，，由于 αχW(x)，故 x∉ W，所以 W'=lα'(χW') ∈ N(x).若 ∃t∈ T － T0使 W'≠ φ，则∃y∈X 使y∉W且αPt(y)≥χW'(y)=1，矛盾.可见，∀t∈T －T0，W'=φ，所以Φ在(X，［δ1］，［δ2］) 中局部有限.则(LX，δ1，δ2) 的底空间(X，［δ1］，［δ2］) 是几乎可数仿紧空间.

(ⅲ)⇒(ⅰ)∀α ∈M(L)，设 Ω 是1X的任一可数 α-δ1δ2远域族，则 lα'(Ω') 是(X，［δ1］，［δ2］) 的可数开覆盖.于是存在(X，［δ1］，［δ2］) 的近似开覆盖 Φ ={Bt|t∈T} 加细 lα'(Ω') 且在(X，［δ1］，［δ2］) 中局部有限.∀t∈ T，∃Qt∈ Ω ，使，令，t∈ T}，则 Ψ 是 Ω 的余加细.∀xα∈1X，∃Bt∈ Φ 使 x∈ Bt，从而 χB't∈ η(xα)，由α'知∈ η(xα)，故 χB't，则 Ψ 是1X的几乎 α-δ1δ2远域族.∀xα∈1X，∃W ∈ N(x) 及有限子集 T0⊂ T，使 ∀t∈ T－ T0，W ∩ Bt=lα'(Ψ).显然 W ⊂ B't，从而 χW≤ χB't≤ χBt'∨ Qt，所以 ∀t∈ T － T0，有(χB't∨ Qt)'≤ χW'∈ η(xα).则 Ψ'∧ A(A ∈ LX) 在 A 中强 α-δ1δ2局部有限.得出结论，L-fuzzy双拓扑空间(LX，δ1，δ2) 是几乎可数层仿紧空间.

推论2 L-fuzzy双拓扑空间中的几乎可数层仿紧集具有“L-好的推广”的性质.

3 几乎可数层仿紧集的性质

定理4 设f∶(LX，δ1，δ2) →(LY，σ1，σ2) 是连续的单满闭的L-Zadeh型函数，α ∈M(L)，若∀A∈LX是(LX，δ1，δ2) 中的几乎可数层 α-δ1δ2仿紧集，则 f(A) ∈ LY是(LY，σ1，σ2) 中的几乎可数层 α-δ1δ2仿紧集.

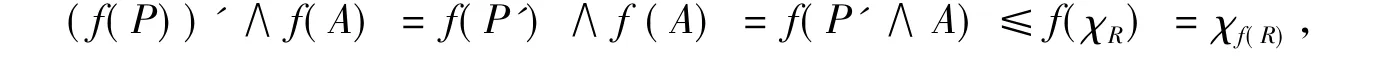
所以(f(Ψ))'∧f(A)在f(A)中强α-局部有限.

定理 5 设 f∶(LX，δ1，δ2) →(LY，σ1，σ2) 是连续的单满闭的 L-Zadeh型函数且 ∀yα∈ M(LY)，(α ∈M(L))，f－1(yα) 是(LX，δ1，δ2) 中的几乎可数层 α-δ1δ2仿紧集.若 B 是(LY，σ1，σ2) 中的几乎可数层 α-δ1δ2仿紧集，则 f－1(B) 是(LX，δ1，δ2) 中的几乎可数层 α-δ1δ2仿紧集.

证明 设α∈M(L)，Ω⊂δ'1∪δ'2是f－1(B)的可数α-δ1δ2远域族，则不难验证f(Ω)是B的可数α-δ1δ2远域族，于是存在B的几乎α-δ1δ2远域族Ψ，使得Ψ是f(Ω)的余加细，且Ψ'∧B在B中强α-局部有限.考虑 f－1(Ψ)={f－1(P) ∶P∈ Ψ}，则f－1(Ψ) 是f－1(B) 的几乎 α-δ1δ2远域族且f－1(Ψ) 是 Ω 的余加细.∀xα∈f－1(B)，存在唯一的y∈Y使f－1(y)=x，yα∈B从而存在分明双拓扑空间中的闭集R∈η－(yα)及有限子集 Ψ0⊂ Ψ 使 ∀P∈ Ψ － Ψ0，P'∧B≤ χR.显然f－1(R)是分明闭集，且 χf(－R1)∈ η－(xα)，由于 f是单、满映射，故 ∀P ∈ Ψ － Ψ0，f－1(P)=f－1(Ψ) － f－1(Ψ0)，且

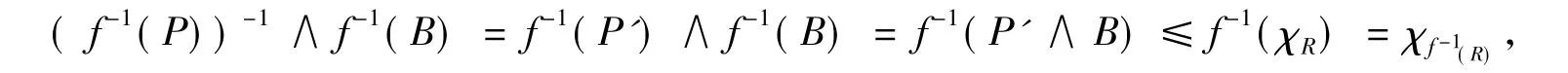
所以 f－1(Ψ))'∧ f－1(B) 在 f－1(B) 中强 α-局部有限.

推论3 L-fuzzy双拓扑空间中的几乎可数层仿紧集具有弱拓扑不变性.

有关L-fuzzy双拓扑空间中几乎可数层仿紧集的进一步研究，我们将在以后的研究中继续讨论.

［1］Kelly J.C.Bitopological spaces［J］.Proc.London Math.Soc，1963，13(3)：71 －89.

［2］张春冰.弱诱导的L-Fuzzy双拓扑空间的分离性［J］.首都师范大学学报，1996，17(3)：68－72.

［3］郑崇友.可拓扑生成的 L-双fuzzy拓扑空间的连通性［J］.北京师范学院学报(自然科学版)，1992，13(2)：1－5.

［4］徐国华.L-双 fuzzy拓扑空间的连通性［J］.模糊系统与数学，1994，(8)：209 －215.

［5］郑崇友，张春冰.弱诱导的L-Fuzzy双拓扑空间的紧致性与连通性［J］.首都师范大学学报，1995，16(4)：5－9.

［6］孟广武.L-Fuzzy拓扑空间中的层仿紧集［J］.模糊系统与数学，1995，9(2)：45 －50.

［7］孙军娜，马保国.L-Fuzzy拓扑空间中的可数层仿紧集［J］.模糊系统与数学，2008，(增刊)：148－152.

［8］孙军娜.L-Fuzzy拓扑空间中的几乎可数层仿紧集［J］.纺织高校基础科学学报，2010，(9)：293－296.

［9］王国俊.L-Fuzzy拓扑空间论［M］.西安：陕西师范大学出版社，1988.