一种基于浓度的粒子群优化算法

李庆芳，孙合明

(河海大学理学院，南京 210098)

粒子群(PSO)算法起源于对简单社会系统的模拟。该算法是1995年由美国电气工程师Eberhard和社会心理学家 Kennedy［1－2］提出的。粒子群算法本质上是一种并行的全局性的随机搜索算法，具有容易实现、搜索速度快、优化性能好等优点［3－8］。该算法自提出以来，引起了国际上相关领域众多学者的关注和研究，并被广泛应用到神经网络训练、工业系统优化及控制［9－12］等领域。

作为一种进化算法，粒子群算法也有其缺点［13］。PSO算法是根据全体粒子和自身的搜索经验向着最优解的方向“飞行”，在进化后期所有的粒子都向“最优点”聚集，趋向同一化，群体的多样性逐渐丧失，致使算法后期的收敛速度明显变慢，甚至处于停滞状态，出现早熟现象。针对PSO算法的这个缺点，本文将免疫算法中基于浓度选择的概率引到PSO算法中，提出一种改进的粒子群算法。该算法根据浓度的大小对粒子的更新进行有选择的指导，从而在一定程度上加快了算法的收敛速度，增强了算法的寻优能力，同时对部分粒子进行初始化，增加种群多样性。实验结果表明，该算法具有较高的优化性能。

1 标准粒子群优化算法

在粒子群算法中，每个个体称为一个粒子，代表着解空间中一个潜在的解。例如，在一个D维的目标搜索空间中，每个粒子看成是空间内的一个点。设群体由m个粒子构成，zi=(zi1，zi2，…，zin)为第 i个粒子(i=1，2，…，m)的D维位置矢量。根据事先设定的适应值函数(与要解决的问题有关)计算zi当前的适应值，即可衡量粒子位置的优劣。vi=(vi1，vi2，…，vid，…，viD)为粒子 i的飞行速度，pi=(pi1，pi2，…，pid，…，piD)为粒子i迄今为止搜索到的最优位置，pg=(pg1，pg2，…，pgd，…，pgD)为整个粒子群迄今为止搜索到的最优位置。在每次迭代中，粒子根据式(1)、(2)更新速度和位置:

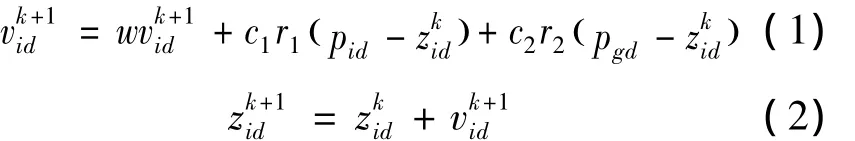
其中:i=1，2，…，m;d=1，2，…，D;k 是迭代次数;w是惯性权重;r1和r2为[0，1]的随机数;c1和c2为学习因子。式(1)的第2项是“认知”部分，代表了粒子对自身的学习，第3部分是“社会”部分，代表着粒子间的协作。式(1)表示粒子根据它上一次迭代的速度、当前位置和自身最好经验与群体最好经验之间的距离来更新速度，然后粒子根据式(2)飞向新的位置。

2 改进的粒子群优化算法

2.1 粒子群浓度的计算

浓度的概念来自人工免疫算法［14］，这是近几年才提出来的一种模拟生物免疫系统的随机优化方法。在求解优化问题时，满足约束条件的最优解即是抗原，候选解即是抗体，抗体与抗原之间的亲和力反映了候选解和最优解得接近程度。为了实现抗体(粒子)的多样性和避免未成熟收敛，采用抗体生存期望值对抗体浓度进行促进和抑制。在种群更新过程中，总是希望适应度高的粒子被保留下来，但是如果此类粒子过于集中，即浓度过高，则很难保证粒子的多样性，很容易使算法陷入局部极优，而丢失那些适应度较差但却保持着较好进化趋势的粒子。因此采用基于浓度机制的多样性保持策略。第i个粒子的浓度［15］定义为

由式(3)可以推导出基于粒子浓度的概率选择公式:

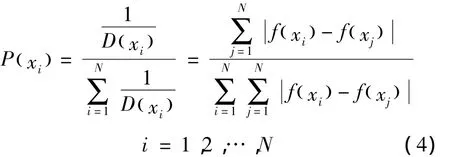
其中xi和f( xi)分别表示第i个粒子及其适应度函数值。由式(4)知，与抗体i相似的抗体越多，抗体i被选中的概率就越小;反之，与抗体i相似度的抗体越少，抗体i被选中的概率就越大。这使得低适应度个体也可以获得进化的机会。因此，基于抗体浓度的概率选择公式在理论上保证了抗体的多样性。

3.2 粒子群的更新策略

当粒子进化到一定程度时，通过引入基于浓度选择的概率公式，避免粒子群陷入局部最优解。将所有粒子的概率按升序排列，排在前面的粒子浓度较高、概率较小，即在空间上该粒子处于较密集的位置，未避免粒子陷入局部最优。给其赋以较大的惯性权重，摆脱个体最优的影响，按照式(5)更新。

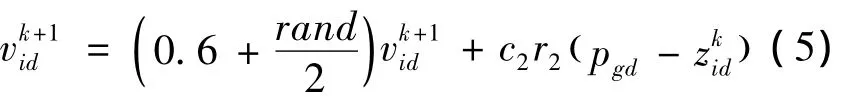
对于浓度较低但概率较大的粒子，根据免疫原理，笔者认为该粒子自身有着很好的进化前景，因此，粒子只受当前自身最优和其自身速度的影响，而忽略粒子的群体最优的作用，速度按照式(6)更新。

为了增加种群的多样性，对其余浓度处于中间位置的部分粒子重新初始化。

3.3 改进的粒子群算法描述

步骤1 初始化参数，确定种群大小N、最大迭代次数itermax、学习因子c1和c2，待求解的为问题维数D、区间长度。

步骤2 初始化种群，即随机产生各个粒子的初始位置和速度。

步骤3 根据目标函数评价每个粒子的适应度。

步骤4 对每个粒子，将其适应度与该粒子经过的个体极值比较，若较好，则将该位置作为当前的最好位置pbest，然后再与整个粒子群经历过的全局极值比较，若较好，则更新gbest。

步骤5 根据速度和位置公式(1)、(2)更新粒子的速度和位置。

步骤6 当种群进化到一定程度时出现停滞，按照式(3)、(4)计算粒子的浓度及概率，并按升序排列:① 选择排列在前个浓度较低的粒子，按式(5)更新速度;② 选择排列在后3个浓度较高的粒子，按式(6)更新速度;③ 其余的6个处于中间位置的粒子，重新初始化，随机赋值。

步骤7 计算更新后的粒子适应度，并更新自身最优解与全局最优位置。

步骤8 判断是否达到最大迭代次数。重复步骤4～6，最后输出全局最优解。

4 测试函数及结果

为测试改进的粒子群算法的性能，本文选择了5个著名的benchmark测试函数对该算法和标准PSO进行对比测试。

F1:著名的Sphere函数，它在xi=0时达到最小值0。

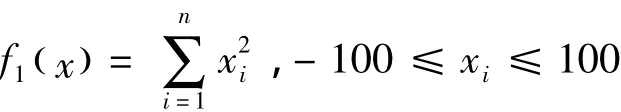
F2:Rosenbrock函数，也叫香蕉函数，一个经典的优化函数，在xi=1处达到全局最小值0。

F3:Rastrigin函数，有很多正弦凸起的局部极小点，在xi=0达到全局最小值0。

F4:Ackley函数，在xi=0时达到全局最小值0。

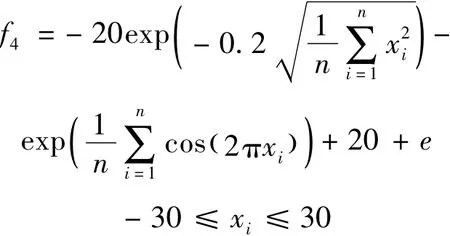
F5:Griewank函数，在xi=0时达到全局最小值0。

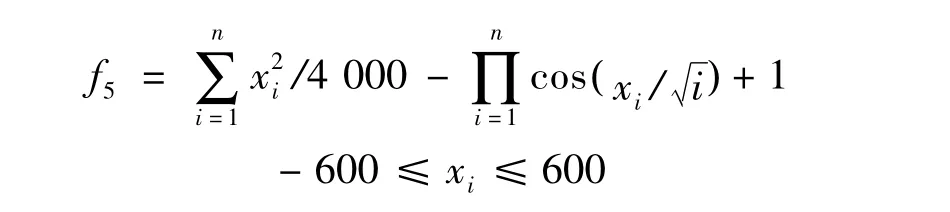
F1是一个连续的简单单模态函数，通常用来分析算法的执行性能。F2是一个经典复杂优化函数，它的全局最优点位于一个平滑狭长的抛物线形山谷内，由于函数仅仅为优化算法提供了少量信息，使算法很难辨别搜索方向，找到全局最小点的机会微乎其微，因此F2通常用来评价优化算法的执行效率。F3、F4是典型的具有大量局部最优点的复杂多峰函数，易使算法陷入局部最优，而不能得到全局最优解。F5是旋转不可分离的多峰函数，类似于 Rastrigin 函数［16］。

试验中 F1、F2、F4、F5的最大进化代数取500，F3的进化代数取1000，维数均取30维，学习因子 c1=c2=1.49445，惯性权重 w 从 0.9 到 0.4线性减少。为方便算法比较，适应值取以10为底的对数。运行结果见图1～5。

图1 F1:Sphere函数的适应度曲线

图2 F2:Rosenbrock函数的适应度曲线

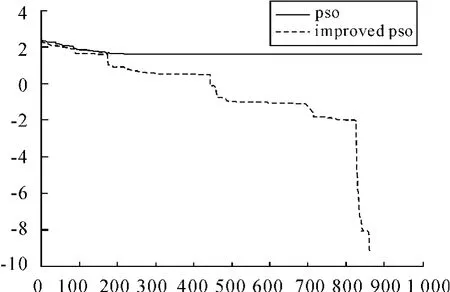
图3 F3:Rastrigin函数的适应度曲线

图4 F4:Ackley函数的适应度曲线

图5 F5:Griewank函数的适应度曲线

从图1～5的实验结果可以看出:改进的PSO比标准PSO有着更好的搜索性能;对于较易收敛的F1和F5，改进的PSO算法收敛速度明显加快，且收敛精度很高;尤其对于比较难于收敛的F3，改进的算法明显优于标准PSO;相对而言F2、F4虽然收敛速度差一些，但收敛精度要好于标准PSO。

5 结束语

标准粒子群算法由于群体的多样性在进化后期变差，从而导致收敛后期速度变慢，易陷于局部最优且收敛精度降低。改进的算法借鉴免疫学习中浓度的概念，按基于浓度的选择概率来指导粒子群的更新，使群体保持了很好的多样性，有效地避免了算法陷于局部最优。实验结果表明，该算法的搜索性能优于标准的粒子群算法。

［1］Kennedy J，Eberhart R.Particle swarm optimization［C］//IEEE Int’1 Conf On Neural Networks.Perth，Australia:［s.n.］，1995:1942 －1948.

［2］Eberhart R，Kennedy J.A new optimizer using particle swarm theory［C］//Proc of the sixth international symposium on Micro Machine and Human Science.Nagoya，Japan:［s.n.］，1995:39 －43.

［3］刘玉敏，俞重远，张建忠，等.粒子群优化算法用于光纤布拉格光栅综合问题的研究［J］.激光杂志，2005(4):69－70.

［4］陈莉，张宏立.粒子群算法在六自由度并联机器人位置正解中的应用［J］.重庆理工大学学报:自然科学版，2010(8):86 －90.

［5］王红玲，郑纲，何剑锋.基于改进粒子群算法的生鲜农产品配送路径优化研究［J］.安徽农业科学，2010(31):17961－17962.

［6］徐传忠，王永初，杨冠鲁.模拟退火粒子群算法的Volterra主动噪声消除器［J］.自动化与仪器仪表，2010(3):116－117.

［7］石玉秋，黄玲，曹乃文，等.基于粒子群算法的喷洒参数优化算法［J］.安徽农业科学，2010(13):6677－6678.

［8］赵吉武，邹长武，卢晓宁.基于粒子群算法的综合暴雨强度公式［J］.安徽农业科学，2010(30):17175－17176.

［9］郭志涛，袁金丽，张秀军，等.基于改进的 PSO神经网络的手写体汉字识别［J］.河北工业大学学报，2007，36(4):65－69.

［10］宁国忠，孟科，颜学峰，等.改进的粒子群算法及其在软测量建模中的应用［J］.华东理工大学学报:自然科学版，2007，33(3):400 －404.

［11］唐英干，刘冬，关新平.基于粒子群和二维 Otsu方法的快速图像分割［J］.控制与决策，2007，22(2):202－205.

［12］杨晶东，洪炳镕，蔡则苏，等.基于粒子群优化的移动机器人全局定位算法［J］.吉林大学学报:工学版，2007，37(6):1402 －1408.

［13］崔志华，曾建潮.微粒群优化算法［M］.北京:科学出版社，2011.

［14］梁鸿生，郝勇娜，王凯等.免疫算法［J］.昆明理工大学学报:理工版，2003，28(5):72 －76.

［15］Gang Lu，De-jian Tan.Improvement on regulating definition of antibody density of immume algorithm［C］//Proceedings of the 9thinternational conference on neural information processing(ICONIP 02).USA:［s.n.］，2012:2669－2672.

［16］赫然，王永吉，王青，等.一种改进的自适应逃逸微粒群算法及实验分析［J］.软件学报，2005，12(16):2036－2044.