金属泡沫内部流动及换热分析

赵佩国，王锁芳

(南京航空航天大学能源与动力学院，南京 210016)

目前，航空发动机上所使用的燃油－滑油散热器基本上是管壳式的，既增加了飞机的质量，换热效率又不高。随着科学技术的发展及制造工艺的提高，一种新的材料——金属泡沫出现了。它是一种典型的低密度新型物理材料，具有很好的导热、导电和力学性能。由于金属泡沫单位体积能提供很大的导热面积及对流体有很高的渗透率，有很高的研究和利用价值。

金属泡沫属于一种多孔介质，分开口和闭口2种，应用在散热器中的属于开口金属泡沫。如图1所示，其微观结构如图2所示。

图1 金属泡沫宏观结构

图2 金属泡沫微观结构

目前，针对金属泡沫的研究方法有2种:①从宏观上进行实验分析理论计算，如Bhattacharya和Mahajan等对金属泡沫材料强迫对流换热问题进行了实验研究。结果表明，对5ppi和20ppi的金属泡沫材料在介质流速为0.5～1.9 m/s的情况下，对流换热系数可达1000 W/(m2K)，而压降只有60 Pa［1］。南京航空航天大学的夏捷等用数值计算的方法模拟了离心力场下装有多孔介质的封闭腔体中的热驱动换热现象。计算结果表明，在封闭腔体中加入大孔隙率多孔介质后确实能起到强化换热的效果，采用的固体介质的导热性越好，封闭腔体中流体的热驱动能力越强，换热效果越好［2］。② 从微观上进行分析，即从金属泡沫每一个单元结构入手，建立相应的几何模型，最早的是立方体模型，如图3所示，但是这种模型过于简单，模拟结果与实验误差相差较大。Boomsma和Poulikakos基于八细胞周期结构将理想的八面体开孔泡沫金属模型细化，并分析了高孔隙率金属泡沫的二维和三维结构，基于热电比拟建立了泡沫铝金属内的有效导热系数模型［3］。本文采用一种新的几何模型来研究高孔隙率金属泡沫内部流动及换热的情况。

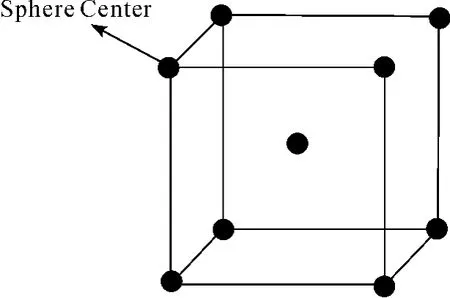
图3 立方体模型

1 几何模型及网格划分

本文采用的金属泡沫数值模型如图4所示，最小重复单元如图5所示。该模型是由边长为a的立方体在其8个顶点和中心点减去半径为R的球体所得(a＜R/2)，流体(滑油)沿Z轴流过由4个最小单元结构组成的长度为L的流道。模型换热面积记为A，体积为V。本文对孔密度为5 ppi和20 ppi的金属泡沫进行数值计算和模拟，具体的结构参数见表1。由于模型结构比较复杂，只能采取非结构方式进行网格划分，并对局部进行加密处理，最小单元体网格如图5所示。

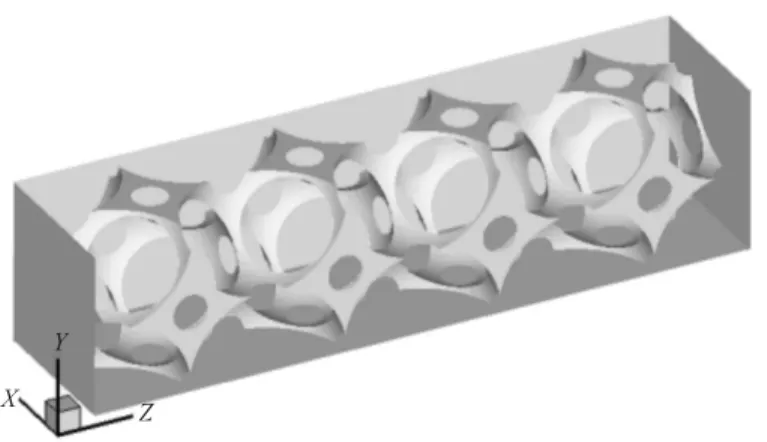
图4 金属泡沫数值模型

表1 金属泡沫数值模型结构参数

图5 金属泡沫单元体网格模型

2 数值模型及边界条件

2.1 控制方程及湍流模型

为了便于模拟和分析，假设:①滑油的物理性质保持恒定，即不随温度的变化而变化;②滑油不可压缩;③滑油在金属泡沫中的流动为湍流。滑油在金属泡沫中的流动和换热由N－S方程控制，在数值模拟时采用标准k－ε模型，具体方程为:

2.2 边界条件

为了使上述方程能得出有效的解，还需要给出进出口边界条件。如图4所示，流体沿Z轴正向流过金属泡沫，进口边界设为速度进口，出口边界设为压力出口，模型底部壁面为加热壁面，边界条件设为wall，恒温，其余3个面设为symmetry边界条件，滑油的物性参数以进口温度为准，金属泡沫为铝合金材料，导热系数为常数，即λw=220 W/(m2·K)。

3 计算结果分析

3.1 计算方法验证

金属泡沫属于多孔介质，在多孔介质中流动阻力可以应用Darcy定律和Forchheimer定律，两者均是根据实验数据得到的经验公式［4－5］。由于在多孔介质中流动很复杂，根据前人实验研究，Darcy定律只适用于低速情况，在流速较高时需要采用Forchheimer定律，表达式为

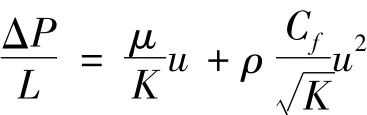
从上式可以看出，ΔP/L是关于u的抛物线方程，且常数项为零，而，则 ΔP/L是关于Red的抛物线方程。从图6可以看出:数值模拟的压力损失曲线经拟合后是抛物线，而常数项和ΔP/L数值相比很小，是由于壁面摩擦产生，因此，本文所选取的数值模拟方法可行。

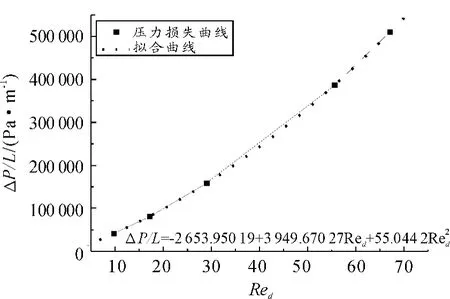
图6 5 ppi总压损失曲线

3.2 滑油在流动过程中的压力变化

滑油在金属泡沫中流动时，由于金属泡沫内部结构比较复杂，压力变化和金属泡沫内部单元结构有很大的关系，如图7所示。

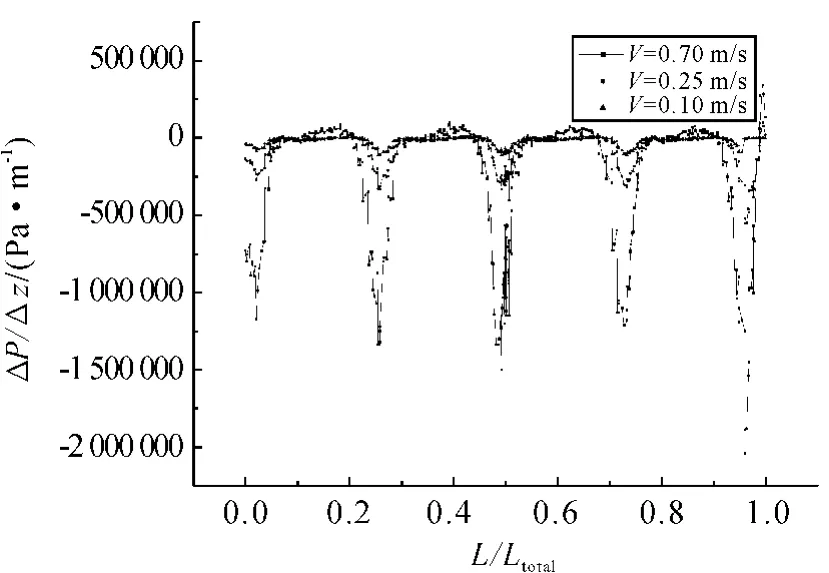
图7 5 ppi当地压力损失变化曲线

从图7可以看出，ΔP/ΔZ数值基本上都是负值，因此，滑油沿着流动方向总压是降低的。滑油从模型中流过时呈现周期性变化，在每一个单元出口和下一单元入口处，压力损失变化最为剧烈，这是由于2个单元之间是由孔连接的，而孔在滑油通过时会产生节流现象，造成压力剧烈变化［6］，在单元内部流动时压力变化不明显。从图7还可以看出:随着滑油速度的增大，压力损失变化幅度增大;随着速度的增大，压力损失在流动方向上的变化就会在开孔处向上下游拓展。

不同的孔密度对压力损失也会产生影响。从图8可以看出，在速度相同的情况下，孔密度为20 ppi的金属泡沫比孔密度为5 ppi的金属泡沫压力损失变化要大很多，但是两者的周期性变化基本一致。从表1可以看出，和5 ppi相比，20 ppi金属泡沫中单元体的孔直径要小很多，当滑油以相同的速度流经这些孔时，所产生的压力损失变化曲线在2个单元连接处变化幅度很大，而5 ppi的变化就平缓很多，但是由于两者的结构类似，所以具有相同的周期性。

3.3 金属泡沫综合性能分析

金属泡沫作为散热器材料，对其综合性能的评价主要从散热器角度进行，具体从摩擦因子f及表示换热能力的Nud两个方面。图9、10分别显示了滑油在金属泡沫中流动时的摩擦因子和传热因子变化曲线。图9中的为金属泡沫的渗透系数［7］。从图9可以看出，在Rek很小时，f随Rek的增大迅速减小，之后，随Rek的增大f变化很平缓。孔密度为20 ppi的金属泡沫的摩擦因子曲线更陡峭，而孔密度为5 ppi的金属泡沫摩擦因子曲线相对平缓。从图9中还可以看出，20 ppi的金属泡沫摩擦因子要稍大于5 ppi的金属泡沫。

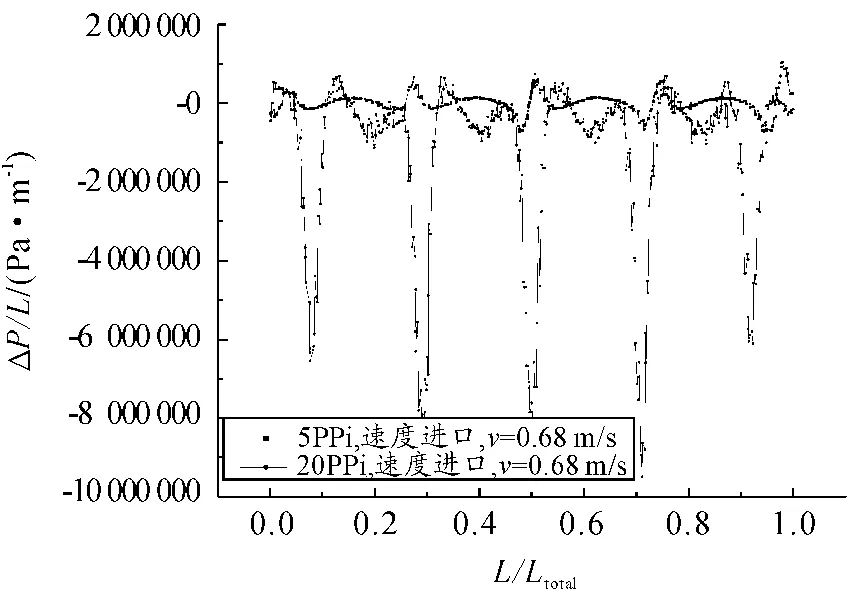
图8 不同款密度当地压力损失变化曲线

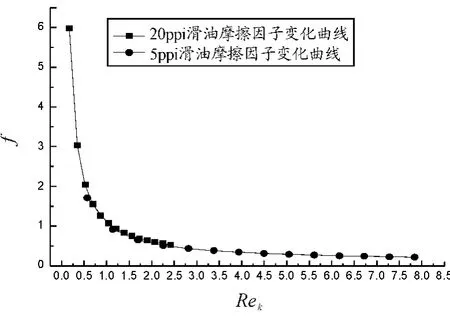
图9 滑油流动摩擦因子变化曲线

图10是 Nud－［Ped/(1－ε)］1/2曲线，其中:Ped=Red·Pr，称为贝莱克数，表征流体对流传热量与导热热量之比，当Pe＞1时，热扩散效应就会很明显［8］，d代表金属泡沫水力直径;ε指金属泡沫的孔隙率。由于滑油的导热系数相对较大，计算所用的金属泡沫孔隙率较高，将换热曲线表示成Nud－［Ped/(1－ε)］1/2的形式可以综合考虑滑油对流和热扩散，同时也考虑了金属泡沫的孔隙率对换热的影响［9］。

从图10可以看出:随着［Ped/(1－ε)］1/2逐渐增大，Nud逐渐增大，但是增加的幅度逐渐减小。由于滑油在对流换热过程中的Pe＞1，因此滑油在金属泡沫中流动时，热扩散效应十分明显，应该加以考虑。从图10可以看出20 ppi的Nud大于5 ppi，这是由于在边界条件一致时，随着孔密度的增大，单位体积的换热面积也逐渐增大，换热效果会更好。

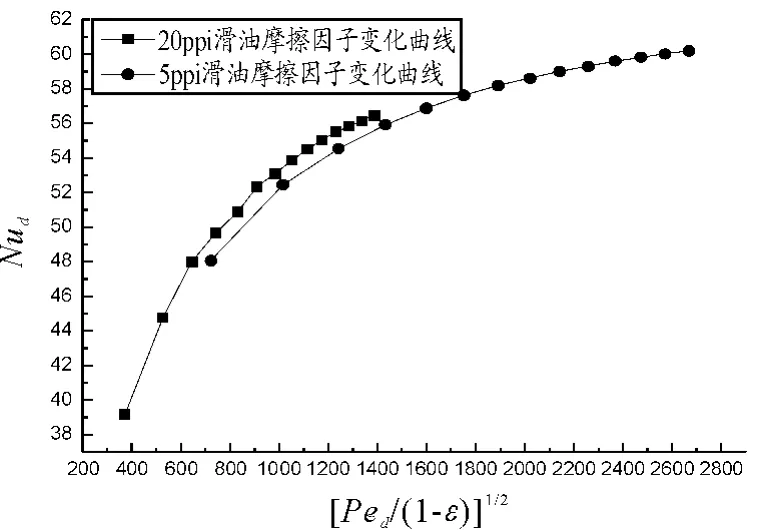
图10 滑油流动Nud变化曲线

综合图9、10可以得出，随着滑油速度的增大，f逐渐减小，滑油由于和换热壁面之间的摩擦而产生的压力损失就会增大，Nud也会逐渐增大。在设计及运行时，要综合考虑金属泡沫的孔隙率、孔密度和流体的速度，以满足生产生活的需要。

4 结论

1)滑油在金属泡沫中流动时会呈现周期性变化;对相同孔密度的金属泡沫，随着滑油速度的增大，压力损失变化幅度也随之增大;当边界条件相同时，孔密度越大压力损失变化幅度越大。

2)随着滑油流动速度的增大，摩擦因子随之减小，但变化曲线会越来越平缓。

3)随着滑油流动速度的增大，Nud逐渐增大，增加的幅度逐渐减小。在滑油流动换热过程中由于Pe＞1，因此必须要考虑滑油自身的热扩散现象。

［1］Bhattacharya A，Calmidi V V，Mahajan R L.Thermophysical properties of high porosity metal foams［J］.Heat Mass T ransfer，2002，45:1017.

［2］夏捷，常海萍.装有多孔介质的封闭腔体中热驱动换热的数值研究［J］.南京航空航天大学学报，2005，37(6):699－703.

［3］XIA Jie，CHANG Hai-ping.Numerical Simulation on Thermally Driven Heat Transfer in Enclosure Filled with Porous Medium［J］.Journal of Nanjing University of Aeronautics ＆ Astronautics，2005，37(6):699 －703.

［4］Boomsma B，Poulikakos K.On the Effective Thermal Conductivity of a Three Dimensionally Structured Fluid-Saturated Metal Foam［J］.Heat Mass Transfer，2001，44:827－836.

［5］Darcy H.Les fontaines publiques de la ville de Dyon［M］.［S.l.］:Victor Dalmont，1856.

［6］Missirlis D，Yakinthos K，Palikaras A，et al.Experiment and numerical investigation of the ow eld through a heat exchanger for aero-engine applications［J］.International Journal of Heat and Fluid Flow，2005，26:440 －458.

［7］Boomsma K，Poulikakos D.The effects of compression and pore size variations on the liquid ow characteristics of metal foam.Journal of Fluids［J］.Engineeringe Transactions of the ASME，2002，124:263 －272.

［8］Calmidi V V，Mahajan R L.Forced Convection in High Porosity Metal Foams［J］.ASME Heat Transfer，2000，122:557－565.

［9］Koch D L，Brady J F.The Effective Diffusivity of Fibrous Media［J］.AIChE，1985，32:575 －591.

［10］Paek J W，Kang B H，Kim S Y，et al.Effective Thermal Conductivity and Permeability ofAluminum Foam Materials［J］.Thermophys，2000，21:453 －464.