轴向运动黏弹性夹层板非线性动力稳定性分析

李映辉，吕海炜，李中华，李 亮

(1.西南交通大学力学与工程学院，成都 610031;2.中国石油宝鸡石油机械有限责任公司，陕西宝鸡 721002)

很多学者在黏弹性夹层板和轴向运动结构方面做了大量工作。在黏弹性夹层板方面，Cheung和Khatua［1］基于经典层合板理论，提出了夹层为正交各向异性材料的夹层板有限元计算方法，并分析了夹层板的稳定性;沈和冷［2］采用 Kelvin-Viogt模型和等参元法，分析了黏弹性夹层板结构的边界条件、阻尼层位置对结构动力特性的影响;李等［3］将有限元与非线性数值拟合相结合，得到了黏弹性阻尼夹层板的谐振频率、损耗因子的近似表达式，提出了基于灵敏度分析的黏弹性阻尼夹层板优化设计方法。在轴向运动结构方面，Chen和Yang［4］利用多重尺度法研究了轴向运动黏弹性梁的稳定性;Marynowski［5］通过对受时变张紧力作用的轴向运动黏弹性梁的数值仿真，比较了Kelvin模型、Maxwell模型以及Bügers模型的黏弹性梁的非线性;Marynowski［5］通过对受时变张紧力作用的轴向运动黏弹性梁的数值仿真，比较了Kelvin模型、Maxwell模型以及Bügers模型的黏弹性梁的非线性振动。目前，将黏弹性夹层板和轴向运动结构结合起来进行的研究较少，周等［6－7］研究了运动黏弹性板的横向振动及稳定性，考虑随从力作用的运动黏弹性板的动力稳定性;Hatami［8］使用精确有限元条法研究了轴向运动黏弹性板的自由振动;李［9－10］利用 Galerkin截断研究了小变形下轴向运动黏弹性夹层板的横向振动。本文将通过建立大挠度下轴向运动黏弹性夹层板横向振动控制方程，研究其横向振动特性，讨论了轴向运动速度对其稳定性的影响。

1 轴向运动黏弹性夹层板控制方程

图1为四边简支轴向运动黏弹性夹层板，其上下为对称约束层，厚度为h/2，中间层为夹心层，厚度为H，夹层板以速度ve沿x轴运动。其中上下约束层为弹性材料，密度为ρc，弹性模量为Ec，泊松比为μc;夹心层为Kelvin-Voigt黏弹性材料，密度为 ρj，弹性模量为 Ej，泊松比为 μj，黏弹性阻尼系数为 η，其等效密度 ρ=(hρc+Hρj)/(H+h)。

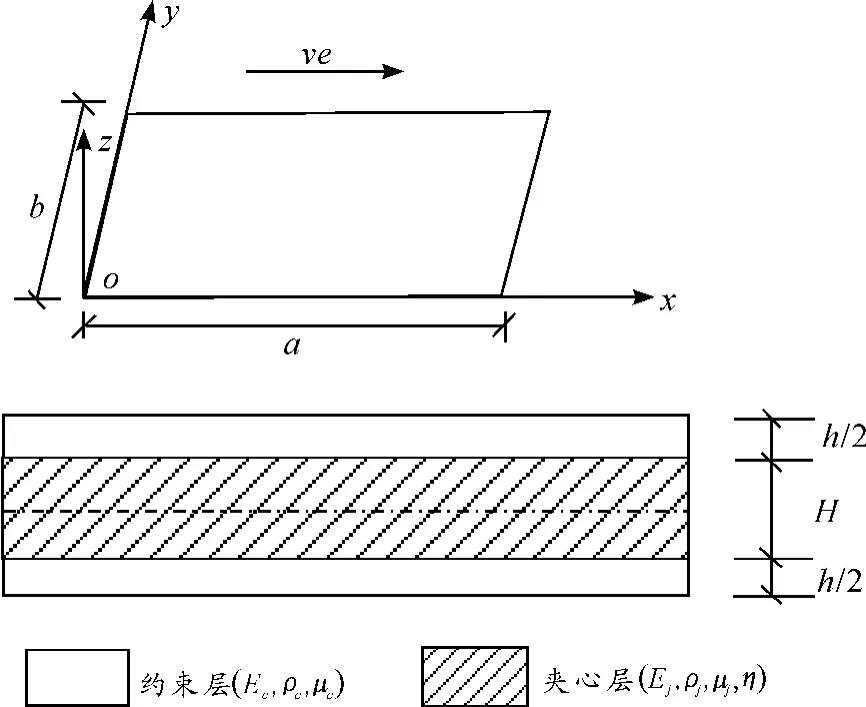
图1 轴向运动黏弹性夹层板模型

文献［9－10］中考虑几何非线性，黏弹性夹层板应变 εx、εy、γxy与挠度 w 的关系为:

可得到大挠度下轴向运动黏弹性夹层板横向振动控制方程:

其系数见附录。

2 Galerkin离散

对四边简支壁板，边界条件为

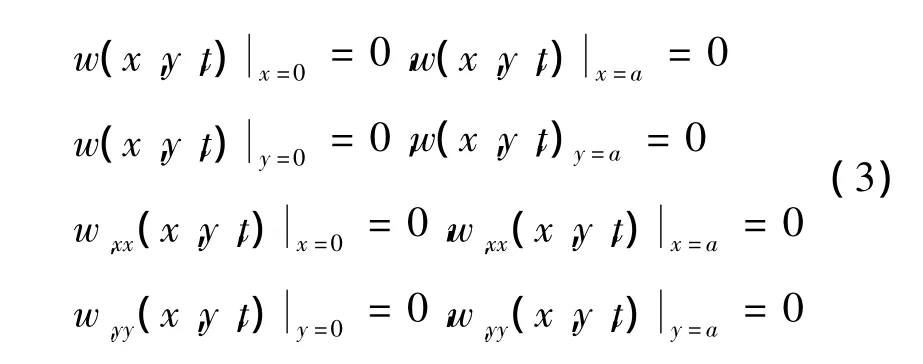
设方程(3)解的形式为

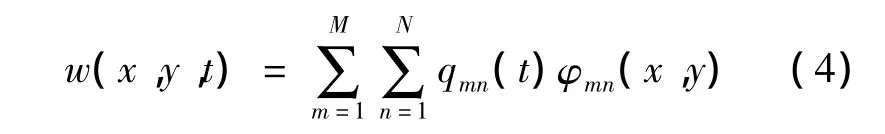
其中:φmn(x，y)是满足边界条件的试函数;M、N为截断阶数。在四边简支条件下通常取

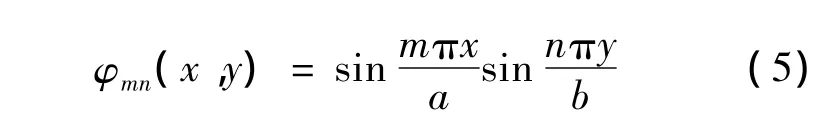
将式(5)代入方程(3)，得系统的残差R(x，y，t)(详细表达式见文献［11］)。使用Galerkin方法

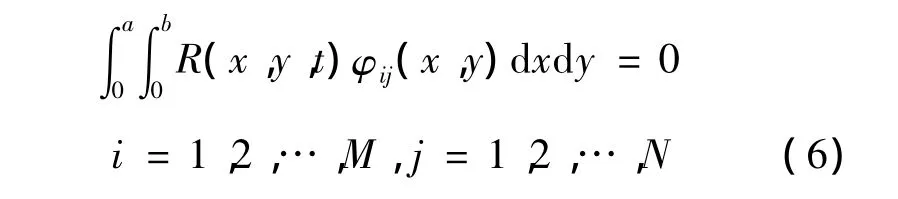
2.1 一阶截断方程

当M=1，N=1时，得一阶截断常微分方程，令x1=q11(t)，x2=˙x1，将式(3)写成矢量形式˙x=f( x)，x∈R2

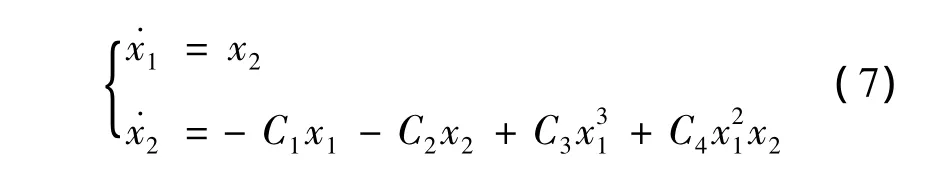
其系数见附录。

2.2 平衡点及其稳定

由式(7)可得系统平衡点为

2.3 结果

轴向运动黏弹性夹层板的几何及材料参数见表1和表2。

表1 黏弹性夹层板几何参数

表2 黏弹性夹层板材料参数

图2给出了平衡点随轴向运动速度变化，可以看到，平衡点的个数在轴向运动速度ve=68.5 m/s处发生改变，在此之前只有1个平衡点X1，之后变为3个平衡点X1、X2和X3。表3给出了不同轴向运动速度下系统的平衡点以及特征值，可以看到在轴向运动速度ve=68.5 m/s处平衡点的稳定性发生改变，说明临界速度为68.5 m/s。

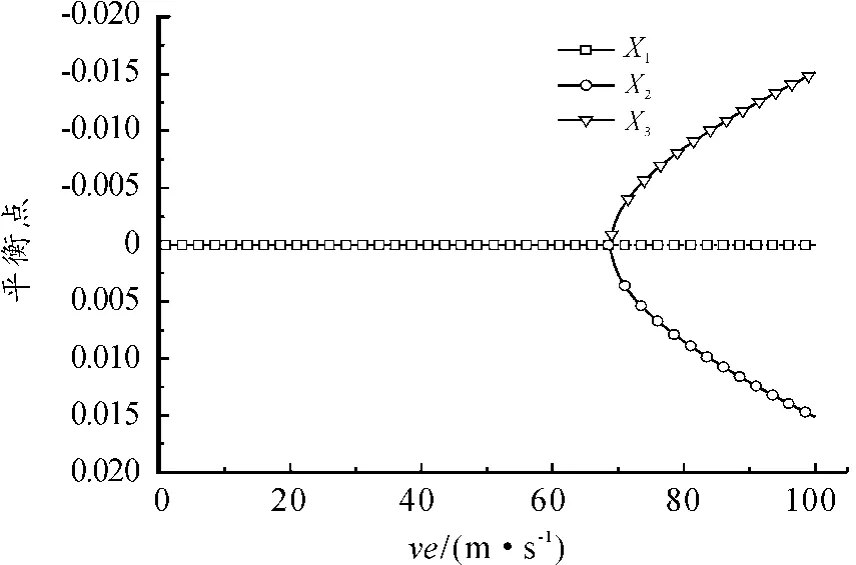
图2 平衡点随轴向运动速度变化的分叉

图3为特征值λ1随轴向运动速度变化情况。当轴向运动速度为零时，特征值λ1的实部为负数。在未到达临界速度之前，特征值虚部随轴向运动速度的增大而减小，到达临界速度后，特征值的实部将会分为两支，虚部变为零，平衡点将由稳定变为不稳定。

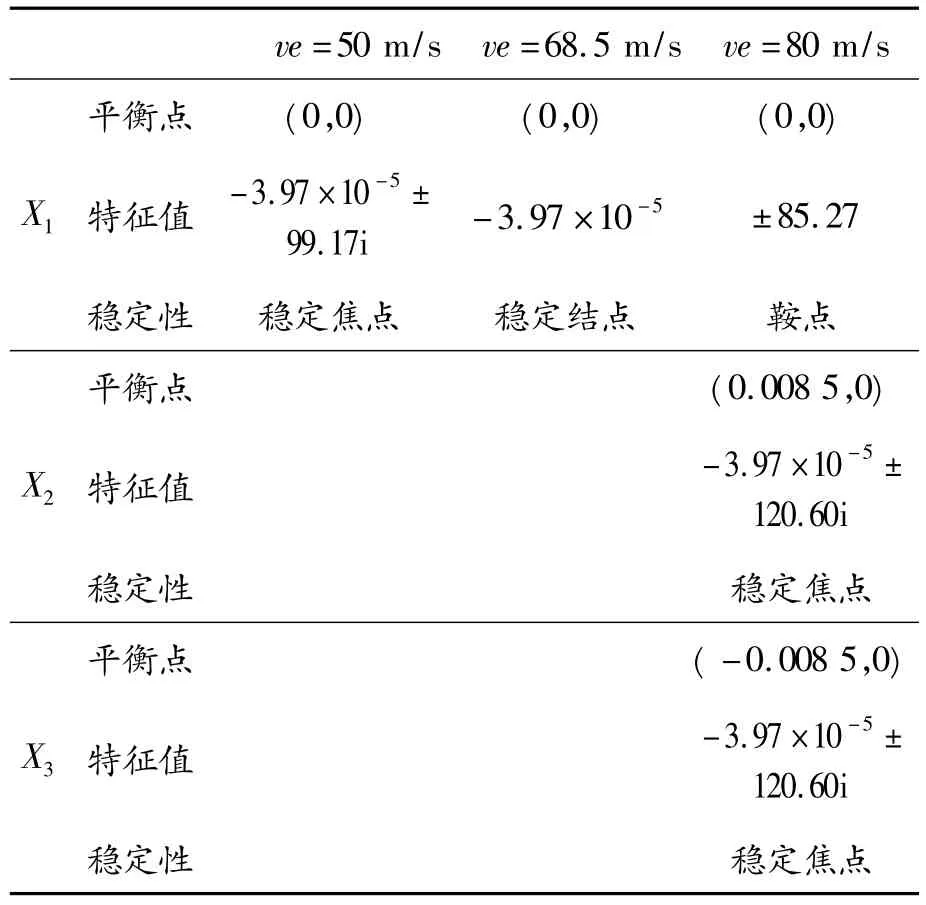
表3 不同轴向运动速度下系统的平衡点特征值及稳定性

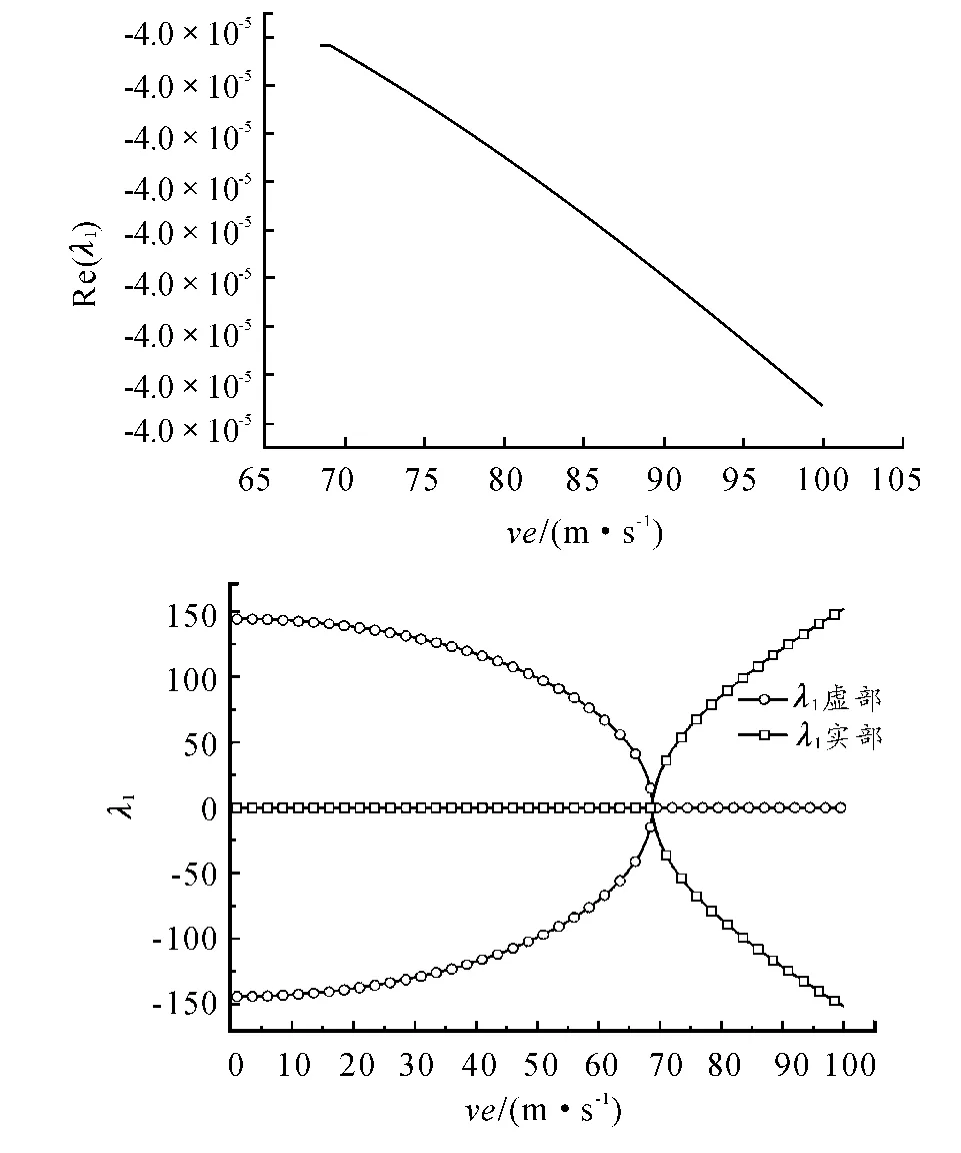
图3 特征值λ1对轴向运动速度变化情况(X1)

图4给出了特征值λ2和λ3随轴向运动速度变化情况，其中特征值λ2和λ3变化规律一样，特征值虚部都是随轴向运动速度的增大也而增大，特征值的实部为一定负值，说明过临界速度后分叉生成的平衡点X2和X3都是稳定的。

图4 特征值λ2和λ3随轴向运动速度变化情况(X2，X3)

3 结束语

基于von-Karmen薄板大挠度理论和Kelvin-Voigt黏弹性本构方程，建立轴向运动黏弹性夹层板横向振动控制方程。使用一阶Galerkin截断方法研究了其非线性方程。其结论为:对与一阶截断，研究了黏弹性夹层板系统平衡点及稳定性随轴向运动速度变化的情况;当轴向运动速度小于临界速度时，系统只有一个稳定的平衡点，平衡点个数在临界速度处发生改变，由1个平衡点分叉为3个平衡点，其中原来的平衡点由稳定变为不稳定，分叉出来的2个平衡点是稳定的。

［1］Kathua，Cheung.Bending and vibration of multi－ layer sandwich beams and plates［J］.International Journal for Numerical Methods in Engineering，1973，6(1):11 －24.

［2］沈顺根，冷文浩.粘弹性线性复合结构动力特性分析［J］.中国造船，1996，133(2):44 －52.

［3］李映辉，林松，高庆.约束阻尼板优化设计方法［J］.重庆工学院学报:自然科学版，2007，21(1):1－6.

［4］Chen L Q，Yang X D.Vibration and stability of an axially moving viscoelastic beam with hybrid supports［J］.European Journal of Mechanics A/Solids，2006，25(6):996－1008.

［5］Marynowski K.Two-dimensional rheological element in modeling of axially moving viscoelastic web［J］.European of Mechanics-A/Solids，2005，25(5):729 －744.

［6］周银锋.运动粘弹性板的横向振动及稳定性研究［D］.西安:西安理工大学，2009.

［7］周银锋，王忠民，王砚.考虑随从力作用的运动粘弹性板的动力稳定性［J］.工程力学，2009，26(1):25－29.

［8］Hatami S，Ronagh H R，Azhari M.Exact free vibration analysis of axially moving viscoelastic plates［J］.Computers and Structures，2008，86(17):1738 －1746.

［9］李中华，李映辉.轴向运动粘弹性夹层板的振动分析［J］.四川大学学报:工程科学版，2011，43(Z2):147－151.

［10］李中华，李映辉.轴向运动粘弹性夹层板的多模态耦合横向振动［J］.复合材料学报，2012，29(3):219－225.

［11］李中华.轴向运动粘弹性夹层板振动分析［D］.成都:西南交通大学，2012.

附录: