一个新三维自治系统的混沌分析及电路模拟

杨留猛，俞建宁，安新磊，张文娟，宫兴荣

(兰州交通大学数理与软件工程学院，兰州 730070)

在过去的几十年，混沌系统的构造一直被人们所关注［1－8］。自从1990年Pecora和Carroll［9］首次采用驱动－响应的方案实现混沌同步，并在电子线路上观察到混沌同步现象以来，混沌同步就成为人们研究的热点。文献［10］根据混沌同步理论从时间序列中构造出了混沌系统模型。文献［11］研究了2个随机耦合RBNS混沌系统的同步现象。Miliou等［12］研究了一个满足混沌同步通信的非线性电子振荡器。Kuntanapreeda.s［13］根据Lyapunov稳定性理论和LMI法构造了一个使2个相同混沌系统同步的控制器。文献［14］利用混沌同步理论对Josephson结进行了有效的控制。

本文首先提出了一个具有复杂混沌吸引子的非线性混沌自治三维系统，采用线性反馈控制方法，通过混沌系统的最大Lyapunov指数确定控制参数的取值范围，避免了构造Lyapunov函数所带来的困难，实现了新系统的同步控制。最后进行了电路实验，验证了混沌吸引子的存在性和同步现象。

1 数学模型

本文构造了一个三维自治混沌系统:

其中:x=(x，y，z)T∈R3为系统的状态变量;a，b，c∈R为参数。系统(1)中只含有2个非线性项。可以验证系统(1)和Lorenz系统族中的每一个系统都不具有拓扑等价性，是一个全新的三维自治混沌系统。当参数a=5，b=4，c=－4时，系统(1)存在一个混沌吸引子，如图1所示。

图1 系统(1)的混沌吸引子

2 线性反馈同步控制及数值仿真

2.1 线性反馈同步

考虑混沌系统:

以系统(2)为主系统，构造从系统:

采用线性反馈后得控制系统:

令E=X－Y，则式(4)可写为

其中:G=［g1，g2，…，gn］T为 N 维非线性函数向量;E=［e1，e2，…，en］T为 N 维误差状态向量;K=diag［k1，k2，…，kn］T为线性反馈控制参数。

定理1 设k=k1=k2=…=kn，系统(2)的最大Lyapunov指数为λmax，则当k＞λmax时‖E‖ =0。

本文定义▽V(X)为系统(2)的向量场散度。

由式(4)得

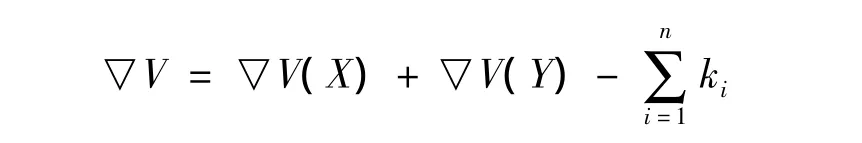
由式(5)得

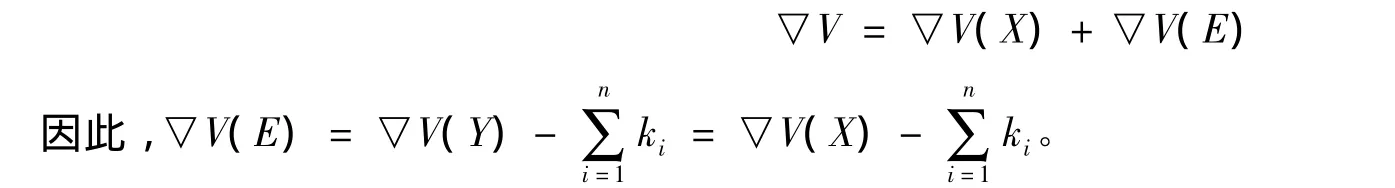
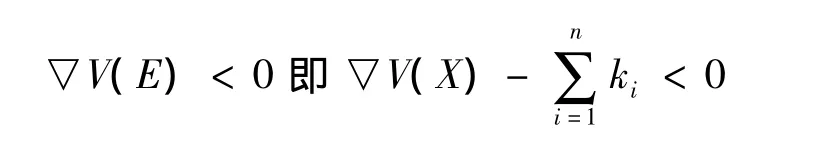
又因为k=k1=k2=…=kn，所以k＞λmax，定理1得证。

2.2 新系统的数值仿真

下面构造受控系统:

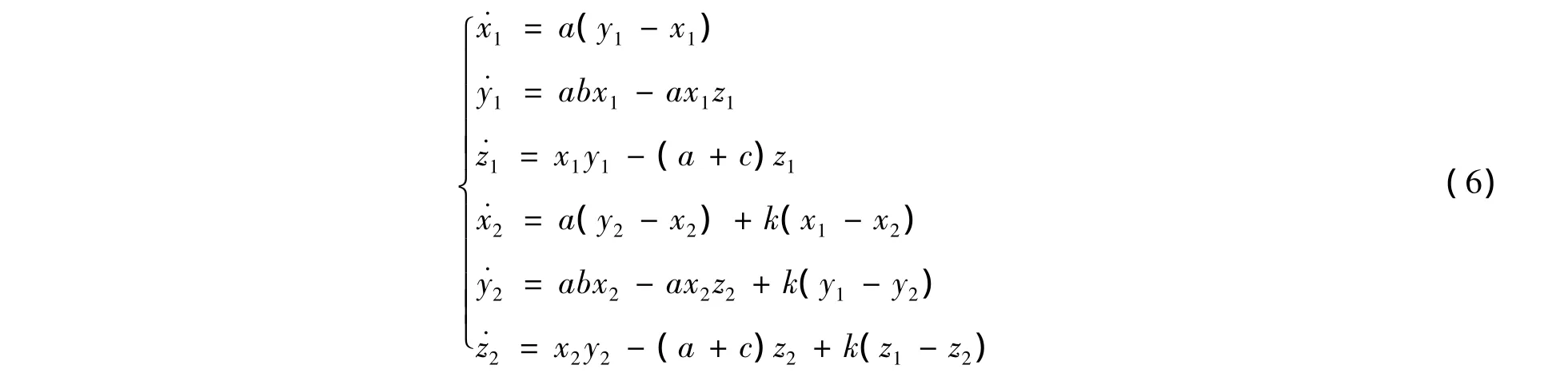
其中k为线性耦合系数。

定义状态误差信号

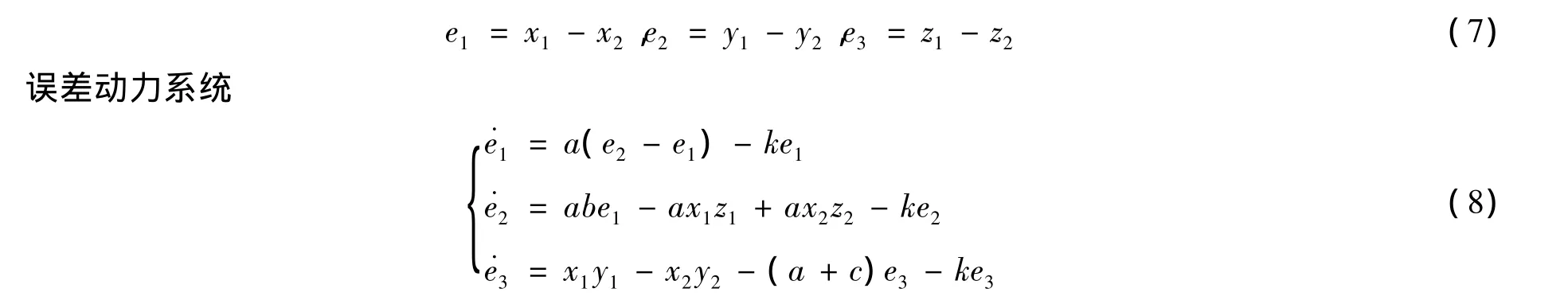
直接参照定理1来求取满足同步条件的k值。当a=5，b=4，c=－4时，可以很容易地求出系统(1)的最大Lyapunov指数λmax=0.5888。当k＞0.5888时，可以实现系统(6)的同步控制。

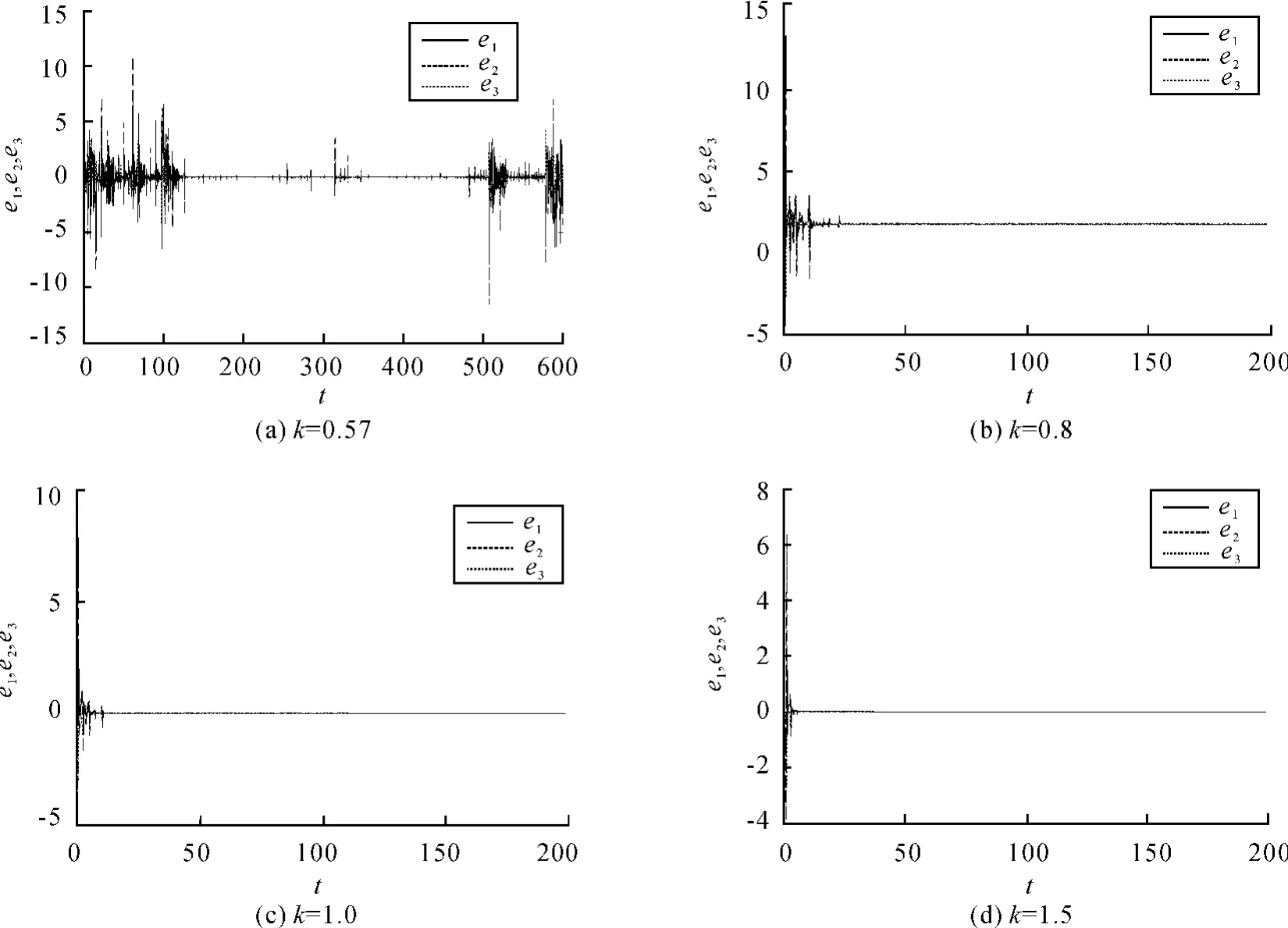
图2 k取不同值时系统(6)的同步误差曲线

3 电路实验

混沌系统的最直接、最简单的物理实现是通过电路来完成的，许多混沌系统的动力学行为都是通过电路得到的验证［15］。基于电子电路设计原理，设计了混沌系统(2)在a=5，b=4，c=－4时的电路，如图3所示。电路中的运算放大器型号为TL084CN，乘法器型号为AD633(增益为0.1)，电源电压值为12 V，其余电路元件参数值见图3。

系统(1)在a=5，b=4，c=－4时的电路方程为

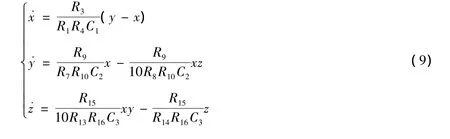
图3 系统(1)在a=5，b=4，c=－4时的电路

根据图3所示的电路进行电路实验，分别在输出端口接入示波器，得Multisim10.0仿真相图，如图4所示，这与图1的Matlab数值仿真结果一致。

图4 系统(1)在a=5，b=4，c=－4时的电路实验相图

通过加入线性反馈电路也可以得到系统(6)的电路，如图5所示。

图5中:R1=R2=R14=R16=R19=R20=R30=R32=100 kΩ;R3=R8=R9=R13=R15=R21=R26=R27=R29=R31=10 kΩ;R4=R10=R22=R28=20 kΩ;R7=R25=25 kΩ;R5=R6=R11=R12=R17=R18=R23=R24=R33=R34=R35=R36=R37=R38=R39=R41=R42=R43=R45=R46=R47=1kΩ;C1=C2=C3=C4=C5=C6=1 μF。

当 R40=R44=877.19 kΩ，R48=175.44 kΩ 时，k=0.57;当 R40=R44=625 kΩ，R48=125 kΩ 时，k=0.8;当 R40=R44=500 kΩ，R48=100 kΩ 时，k=1;当R40=R44=333.33 kΩ，R48=66.67 kΩ 时，k=1.5。当k取不同值时，系统(6)的同步误差曲线如图6所示。由此可见，电路实验与数值仿真结果相一致，系统(6)的同步电路是真实存在的。

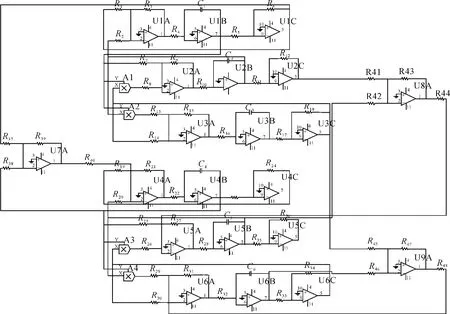
图5 系统(6)在a=5，b=4，c=－4时的电路

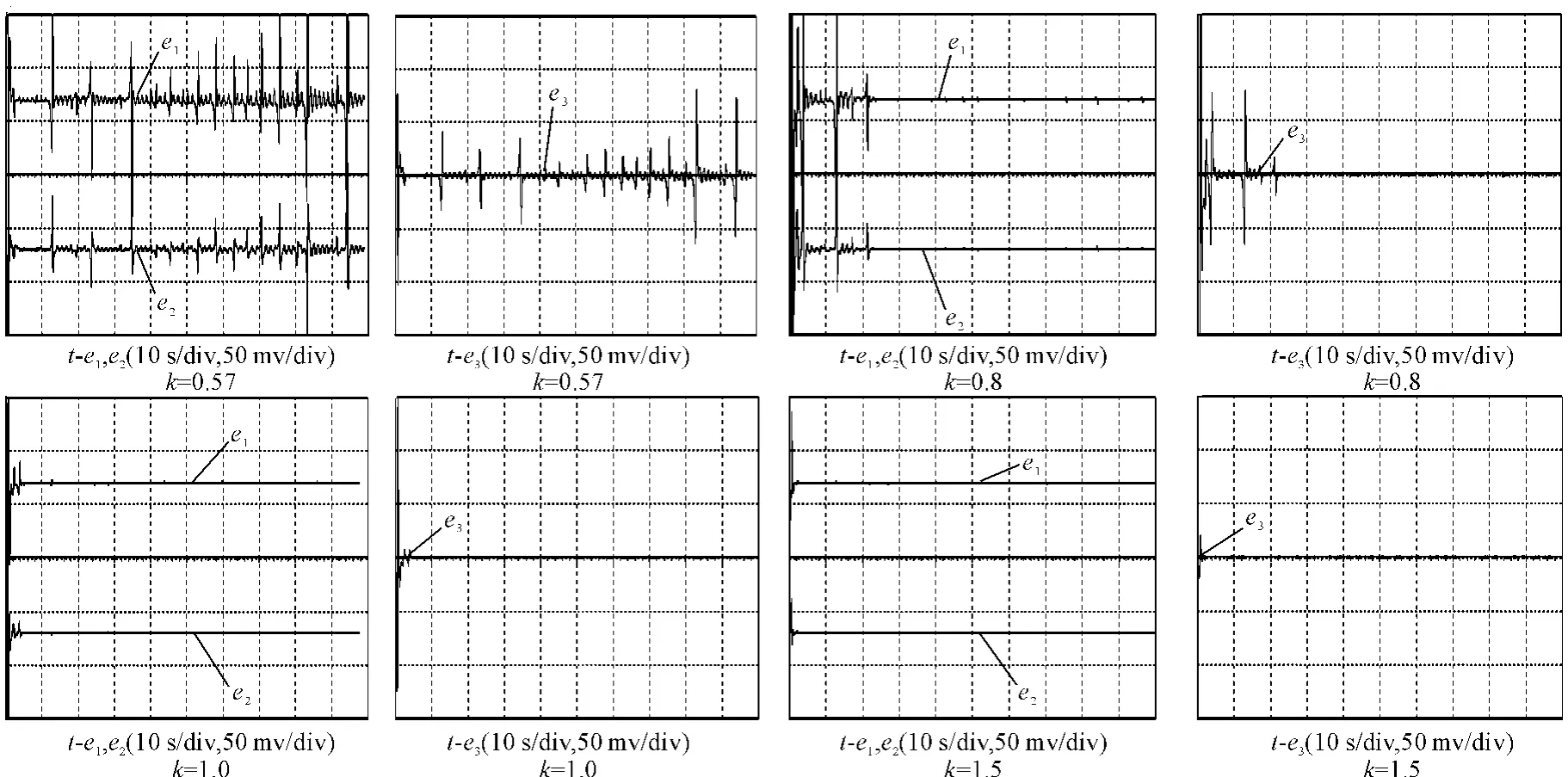
图6 系统(6)的同步误差曲线

4 结束语

本文首先提出了一个非线性混沌自治三维系统以及线性反馈控制同步的思想，从理论和数值2方面对线性反馈同步控制进行了分析和仿真。结果表明，该控制方法具有普适性，可以应用于其他的混沌系统的同步控制当中。最后利用电路仿真软件对新系统的一个吸引子及其同步进行了仿真，达到很好的效果。

［1］陈关荣，吕金虎.Lorenz系统族的动力学分析、控制与同步［M］.北京:科学出版社，2005.

［2］刘凌，苏燕辰，刘崇新.一个新混沌系统及其电路仿真实验［J］.物理学报，2006，55(8):3933－3936.

［3］周平，危丽佳，程雪峰.只有一个非线性项的超混沌系统［J］.物理学报，2009，58(8):5201－5208.

［4］Li X F，Chu Y D，Zhang J G.Nonlinear dynamics and circuit implementation for a new Lorenz－ like attractor［J］.Chaos，Solitons and Fractals，2009，41:2360 －2370.

［5］舒永录，孔昭毅.一个新超混沌系统的自适应滑模变结构控制［J］.重庆理工大学学报:自然科学版，2010，24(11):109－112.

［6］孙连新，王忠林，韩敬伟.一个新的三维混沌系统分析及电路实现［J］.四川兵工学报，2010(2):116－118.

［7］叶志勇，邓存兵，江华南.非自治混沌系统中时滞的反馈控制和应用［J］.重庆理工大学学报:自然科学版，2011，25(1):85－90.

［8］胥红星.一个简化Lorenz混沌系统的全局吸引集及应用［J］.四川兵工学报，2011(7):143－146.

［9］Boccaletti S，Kurths J，Osipov G，et al.The synchronization of chaotic systems［J］.Physics Reports，2002，366:1 －101.

［10］Tao C，Zhang Y，Du G H，et al.Fitting model equations to time series using chaos synchronization［J］.Phys Lett A，2004，332:197－206.

［11］Hung Y C，Ho M C，Lih J S，et al.Chaos synchronization of two stochastically coupled random Booleannetworks［J］.Phys Lett A，2006，356:35 －43.

［12］Miliou A N，Stavrinides S G，Valaristos A P，et al.Nonlinear electronic circuit［J］.Part I:Multiple routes to chaos Nonlinear A-nal，2009，71:3 －20.

［13］Kuntanapreeda S.Chaos synchronization of unifiedchaotic systems via LMI［J］.Phys Lett A，2009，373:2837 －2840.

［14］Njah A N，Ojo K S，Adebayo G A，et al.Generalized control and synchronization of chaos in RCL-shunted Josephson junction using backstepping design［J］.Physica C，Supercond，2010，470:558 －564.

［15］王发强，刘崇新.Liu混沌系统的线性反馈同步控制及电路实验的研究［J］.物理学报，2006，55(10):5055－5059.