电磁轴承－转子系统的非线性动力学行为分析

吕 宁，李 晶，孟祥雪，张转周

(兰州交通大学，兰州 730070)

1 动力学模型

碰摩是旋转机械的转子与定子之间接触而产生的一种故障现象。碰摩能让静子的间隙增大，叶片断裂，轴承支撑磨损，甚至整个机器破坏瘫痪。近年来，很多学者对轴承－转子系统碰摩故障导致的分岔与混沌现象进行了开拓性的研究［4－7］，其研究结果对旋转机械故障诊断具有很大的参考价值。图1为电磁轴承－转子系统的碰摩力模型。

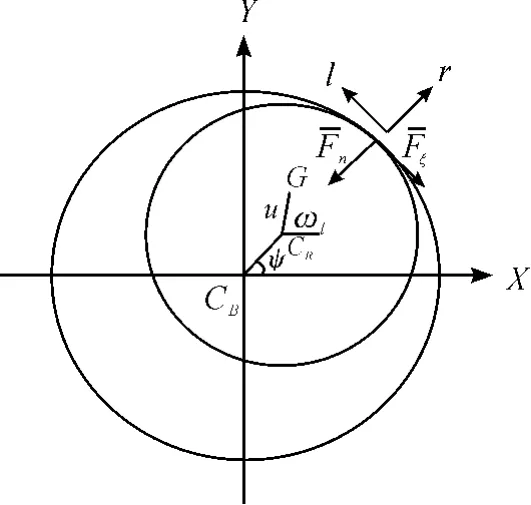
图1 电磁轴承－转子系统的碰摩力模型

首先，假定以下条件成立:

1)由于碰摩时间间隙非常短，因此，摩擦时转子、轴承、机匣的摩擦符合库仑定律，即摩擦力与接触面的法向作用力成正比。

2)忽略回转效应。在考虑到电磁辅助轴承接触力、重力的情况下，系统的运动方程可记为:

其中:m是转子一半的质量;u是偏心量;ω是转子转动角速度。引入无量纲变换后得到的运动学方程为:

2 数值模拟与分析

用标准的Runge-kutta算法对动力学模型进行数值积分，可求得该系统的非线性动力学响应，绘制出不同的偏心量比率U下的分岔图以及特定转速和偏心量下的时间响应图和相图曲线，最后通过分析这些结果，得到关于电磁轴承－转子系统稳定性的一些结论。

图2是以偏心量比率U的变化为基础，通过数值模拟描述的该动力学模型的分岔图，其中参数 Ua=0.05，Ub=0.15，Uc=0.25，Ud=0.35。可以发现随着偏心量比率U的微小变化，系统将呈现出由周期、概周期、混沌等丰富的动力学现象。

下面以图2(d)Ud=0.35为研究对象，通过数值仿真来说明随速度参数ω的变化该系统的非线性动力学行为的变化。

图3、图4 分别取速度参数 ωa=1.400，ωb=1.340，ωc=1.280，ωd=1.120 时，系统所对应的时间响应图和相图。可以明显地看到:系统在ωa=1.400时，其时间响应(图3(a))呈现一周期态，该时刻所对应的相图(图4(a))则表现为一条密封的曲线，可见此时该系统表现为一周期运动;当ωb=1.340时，其所对应的时间响应(图3(b))表现为二周期态，相图(图4(b))表现为2条封闭的曲线，可见此时系统表现为二周期运动;当ωc=1.280时，其所对应的时间响应(图3(c))表现为四周期态，相图(图4(c))表现为4条封闭的曲线，可见此时系统表现为四周期运动;当 ωd=1.120时，其所对应的时间响应(图3(d))表现为无规律波状，相图(图4(d))表现为无数多条曲线相互叠加，可见此时系统表现为混沌态。

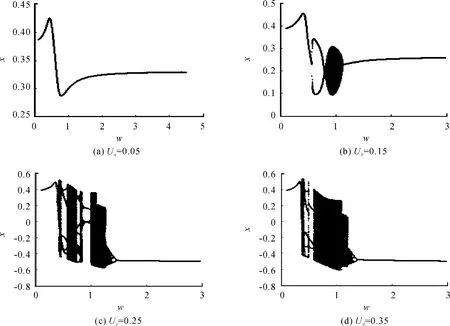
图2 不同偏心量比率下系统的分岔图

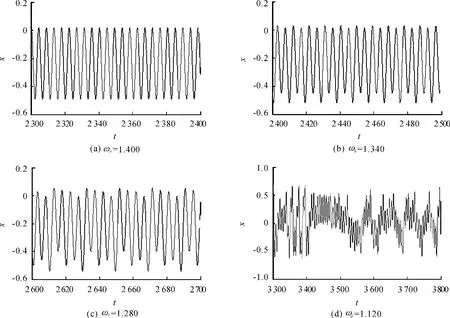
图3 不同速度参数ω下系统的时间响应图

图4 不同速度参数ω下系统的相图

3 结束语

在本文所研究的电磁轴承－转子系统中，通过数值仿真发现该系统对初值变化的敏感度很强，而且很多参数的变化都会影响到系统的运动状态，比如偏心量比率、刚度比率、动摩擦因数等。通过数值仿真发现周期运动、拟周期运动、倍周期分岔、阵发性分岔、混沌等复杂的动力学行为都是系统的主要运动形式，而且混沌运动存在于一个很大的参数空间内。

［1］Jawaid I，Inayat-Hussain.Nonlinear dynamics of a magnetically supported rigidrotor in auxiliary bearings［J］.Mechanism and Machine Theory，2010，45:1651 －1667.

［2］Ishii T，Kirk R G.Transient response technique applied to active magnetic bearing machinery during rotor drop［J］.ASME J Vib Acoust，2010，118:154 －163.

［3］Fumagalli M，Schweitzer G.Motion of a rotor in retainer bearings［C］//Proceedings of the 5th International Symposium on Magnetic Bearings.Kanazawa，Japan:［s.n.］，2009:28－30.

［4］Muszynska A.Stability ofwhirl and whip in rotor bearing system［J］.Journal of Sound and Vibra tion，2008，127(1):58－65.

［5］Edwards S，Lees A W，FriswellM I.The influences of torsionon rotor/stator contact in rotating machinery［J］.Journal of Sound and Vibration，1999，225(4):767－778.

［6］周佳新，罗跃刚.非线性转子系统碰摩的分岔与混沌研究［J］.机械科学与技术，2005(1):6－9.

［7］褚福磊，张正松.碰摩转子系统的混沌特性［J］.清华大学学报:自然科学版，1996，36(7):52 －57.

［8］李振平.多故障转子系统若干非线性问题的研究［D］.沈阳:东北大学，2008.

［9］王追峰，尹忠信，韩天.转子碰摩系统实验研究［J］.应用科技，2010(7):40－43.

［10］袁惠群，闻邦椿，李鸿光.非线性转子局部碰摩故障的分岔与混沌行为［J］.东北大学学报:自然科学版，2008，21(6):610 －613.