基于ASW-TAM的电能质量扰动分析

华贵山，葛 浩

(滁州学院机械与电子工程学院，安徽滁州 239000)

随着各种非线性电力负荷应用的迅猛增长，电能质量问题受到越来越多的关注。其中，对电能质量扰动(power quality disturbance，PQD)进行检测与辨识是对电能质量问题有效治理的前提［1］。而 PQD信号一般是非平稳信号，其特性是随时间变化的。对PQD信号局部信息进行分析，并使用时域与频域的二维联合表示，可以得到更为精确的描述［2］，因此，有必要采用合适的时频分析方法来分析电能质量扰动。

目前，对暂态电能质量扰动分析主要采用时频分析方法，如短时傅里叶变换(STFT)、Wigner-Ville 分布、小波变换(WT)等［3－4］。这些方法在不同程度上对非平稳信号的时变性给予了恰当的描述，改进了傅里叶变换分析方法的不足，但其最终理论依据依然是傅里叶变换，因而不可避免地暴露出某些局限性，如产生虚假频率等现象［5］。此外，许多高分辨谱估计方法也应用于电力系统PQD信号的分析，其分析结果较为精确，但计算量大，实时性差。旋转不变子空间算法(estimating signalparametersvia rotationalinvariance techniques，ESPRIT)［6］和多信号分类(multiple signal classification，MUSIC)算法［7］等是基于信号子空间的空间谱估计方法，近年来被广泛应用于电能质量信号处理领域。较之传统FFT算法，其运算效果更为精确，但是只能用于平稳信号的处理和分析。

本文提出一种基于ASW-TAM的时频分析方法，该方法是对传统TAM的改进，不仅继承了TAM算法精确度高的优点，还可应用于非平稳信号的处理。首先将采样数据进行分块;再对每块中的数据利用TAM算法进行分析，得到频率和幅值信息;最后联合所有窗口的分析结果得到信号整体时频率分布信息。其中，信号的分块是一种自适应的过程，在电能质量扰动出现的位置附近区域采用尽量小的窗口以及滑窗间隔，在平稳信号区域则采用较大的窗口，降低了传统方法运算复杂度，具有较好实际应用前景。

1 基于ASW-TAM的时频分析原理

ASW-TAM应用于电能质量扰动信号分析，首先可定义PQD采样信号模型为

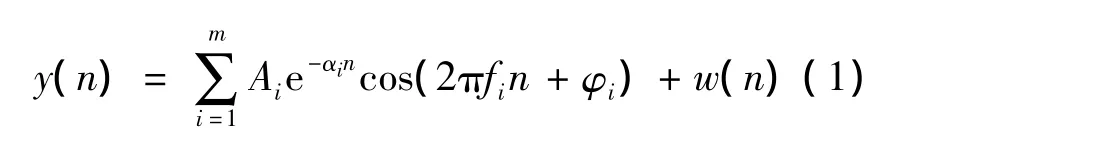
其中w(n)为信号噪声。模型中的信号源数目m是未知的，每个信号源中包含幅值Ai、频率fi、衰减系数 αi和初始相位 φi，其中 i=1，2，…，m。

1.1 自适应滑窗确定

将非平稳PQD信号的数据采样进行合理分块，则每块中的数据可近似看成稳态，因此，可利用TAM算法对每块数据进行处理［8－9］。

首先，对扰动信号进行快速定位［10］，再对采样信号进行后差分，得到

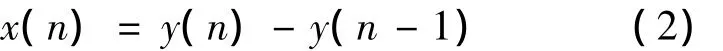
式中:n为采样点数;y(n)为第n次采样的信号幅值;x(n)为近似的差分值序列，即信号连续采样点之间的变化值。

然后，将采样序列 y(n)，n=0，1，…，进行加窗分块，尺寸大小为L，且相邻2块的重叠部分为K(K＜L)，L－K即为滑窗间隔。第j块中的第m个数据采样模型为 y(j)(m)，m=1，2，…，L －1，j=1，2，…。第j块中的数据样本y(j)(m)与原始数据序列中的样本x(n)有关，关系式为

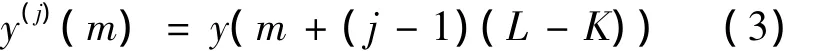
加块数据样本y(j)(m)中的参数m与原始序列中的采样点数n相关，关系式为

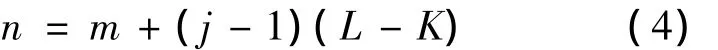
式中窗口变量L、K自适应情况如下:

1)当x(n)＜Mth(阈值)时，采样信号z(n)无扰动变化。检测x(n)连续小于Mth的区域，记起止位置分别为 xst、xed，即平稳信号区域区间为(xst，xed)，有:

式中定义ξ为窗口密度常数，表示该区域内有ξ个滑窗，则滑窗间隔L－K与xed－xst成正比，即平稳区域区间范围越大，滑窗间隔越大，当k=0时，为固定窗。

2)当x(n)≥Mth时，采样信号y(n)出现扰动现象。此时x(n)为扰动定位点，扰动突变附近区域同理为(xst，xed)。令该区域范围为扰动定位点左右各延伸半个周波T/2的长度，则xst=x(n)－T/2，xed=x(n)+T/2，x(n)＞ T/2。将 xst、xed代入式(6)，可得

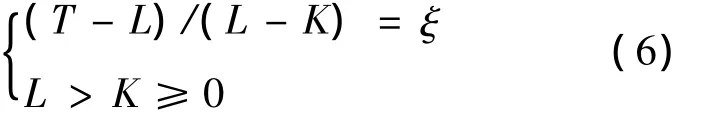
式中滑窗间隔L－K=(T－L)/ξ。

最后，利用结合最小二乘法的TAM［11］算法对每块中的数据进行处理。

1.2 非平稳电能质量扰动信号的幅频检测

设信号y(n)为非平稳PQD信号分块后得到的样本数据，由m个谐波和一个高斯白噪声组成:

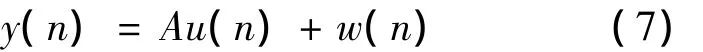
式中:u(n)代表包含m个谐波的信号;w(n)为高斯白噪声。可将u(n)表示为

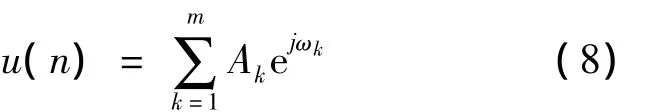
定义向量:

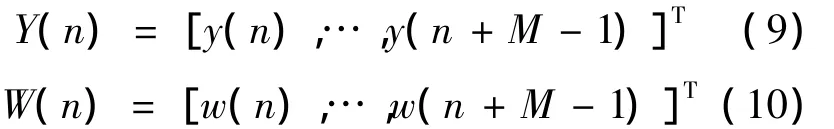
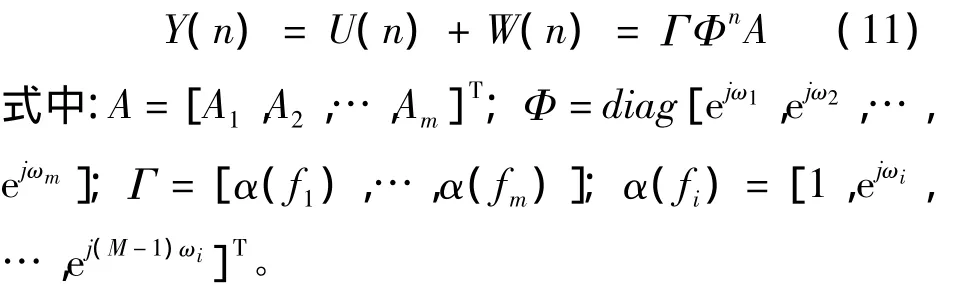
旋转矩阵Φ包含了信号的频率信息，在空间谱估计中称为旋转因子。求取Φ，便可得到信号的频率，进一步可求得各频率信号的其他参数。令

Γ1、Γ2为2个相互联系的M－1维子空间，由式(12)、(13)可得

便可求得旋转矩阵Φ。

本文提出的TAM算法，首先生成数据矩阵，对它进行非奇异值分解，得出子信号与噪声信号子空间，再利用总体最小二乘法求解旋转因子。具体实现步骤:

1)对信号进行采样，时间窗口长度为M，构造L×M的数据矩阵:

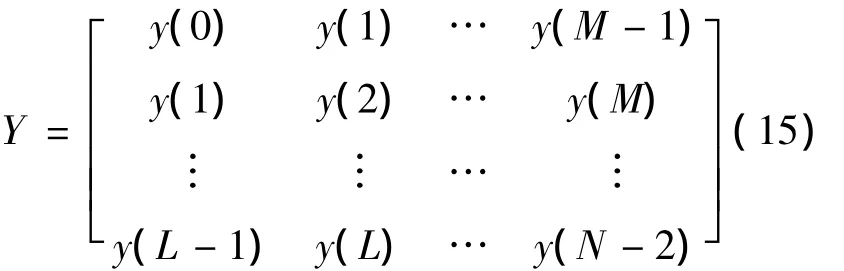
式中:M＞P;L+M=N，N为采样的数目。

2)计算Y的协方差矩阵:

3)对R进行奇异值分解可得

导线、绝缘体、接点、接插件等基本要素与电气元件联结，构成了各种各样的电气设备，这和机械设备的构成不一样。导体、半导体、绝缘体是电气设备的基本组成部分。因此在电气设备使用时，就具有相应的特殊要求。

式中:L为L维左奇异矩阵;V为M维右奇异矩阵;Σ为L×M维奇异值组成的对角阵。

按奇异值大小划分信号子空间V1和噪声子空间V2;Σ1和Σ2对应信号子空间和噪声子空间的奇异值组成的对角阵，Σ1的对角元素远大于Σ2的对角元素;L1和L2对应信号子空间和噪声子空间的特征矢量［12］。

无噪声情况下的数据协方差矩阵为

4)利用旋转不变性思想，通过权矩阵Σ1/21构造新的矩阵，令

可将M维的矩阵Γ分为2个M－1维的子空间，

式中L11和L12分别为L1的前M－1行和后M－1行，可以推得最小二乘解为

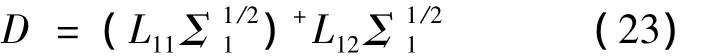
利用D的特征值λm，就可得到旋转因子Φ和其对角元素为λm，从而便可得出原信号中各个分量的频率fm，具体公式为

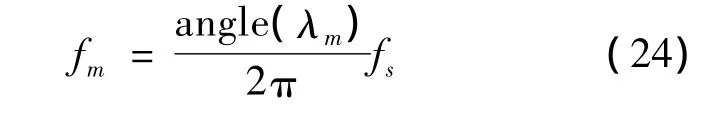
式中fs为抽样频率。

式(7)的矩阵形式为

式(26)的Vandermonde矩阵A的各列是两两线性无关的，即Vandermonde矩阵列满秩，可得式(26)的最小二乘解为［13］

1.3 基于ASW-TAM的算法流程

对电能质量扰动采用一种差分方程分析方法进行快速定位。采用较小窗口及滑窗间隔对扰动位置附近的数据选取数据块，数据为近似平稳信号。采用较大窗口及滑窗间隔来对平稳信号区域划分数据块。利用扩展PRONY算法和TAM算法估计非平稳信号每个数据块中的幅值和频率。最后综合所有窗口的参数信息，便能得到整个时间域内频率分布信息。算法的具体过程如图1所示。

2 仿真实验

为了对非平稳PQD信号进行分析，分别模拟了电压暂降、电压暂升、电压中断、暂态振荡和动态谐波等扰动信号，如图2(a)、图3(a)所示。采样频率12.8 kHz，基波频率50 Hz，取20个周波的波形数据，波形时间为0～0.4 s。阈值 Mth为0.4，窗口密度常数ξ为160，相邻2窗的重叠部分K为3L/4。

图1 ASW-TAM算法流程

2.1 电能质量扰动检测

对电压暂降、电压暂升、电压中断和暂态振荡4种非平稳PQD信号采用以下模型:

ASW-TAM对各种电能扰动信号进行时频分析，可得实验结果见图2(b)、图2(c)，其中:x轴表示时间;y轴表示频率;z轴表示幅值。图中谱线颜色按图2(c)中的色阶对应相应的幅值大小。由图2可得，信号标称电压为1。在38.7～100 ms，信号基波频率为 50 Hz，幅值突变为 1.4996，信号在此期间出现电压暂升。在160～210 ms，信号基波频率为50 Hz，幅值突变为0.6，信号在此期间出现电压暂降。而在270～315 ms，信号基波频率为0 Hz，信号在此期间出现电压中断。在349 ms时刻，信号频率为 122.0014 Hz，幅值为 1.15。信号频率偏离基波频率50 Hz，此时出现振荡脉冲。

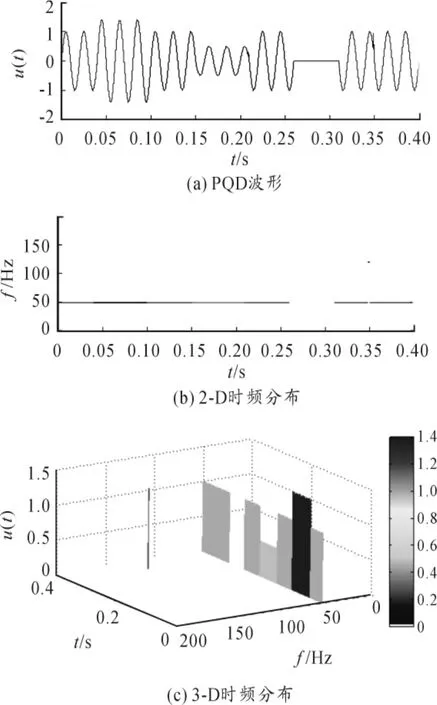
图2 PQD波形及检测结果

为了量化算法的精确度，综合考虑各次谐波和间谐波分量，采用式(29)定义一个相对误差。

式中:Er为相对误差;R(i)为仿真信号的各频率或幅度大小为经过算法分析得到的信号的频率或者幅度平均值。可得如表1所示的误差分析结果。

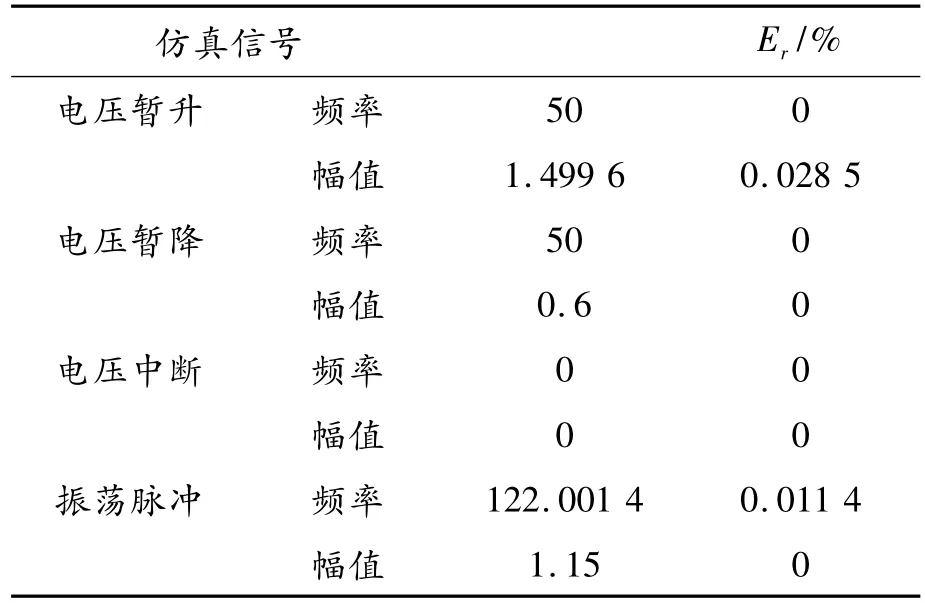
表1 PQD检测误差分析结果

2.2 动态谐波检测

动态谐波信号波形见图3(a)，信号模型由式(30)表示。

如图3(b)、3(c)的时频分布结果所示:在0～48 ms，信号基波频率为50 Hz，谐波频率为150 Hz和250 Hz，幅值分别为 1、0.3 和 0.15;而在 48 ～100 ms，信号基波频率为50 Hz，间谐波频率为115 Hz，谐波频率为 200 Hz，幅值分别为 0.7、0.14 和0.1196。

为了验证算法的正确性，取仿真实验中动态谐波信号，如图3(a)所示。采用STFT时频分析方法对其进行分析，与本文算法进行比较。图4(a)、图4(b)为STFT时频分析结果。

如图4(a)、图4(b)所示:在0 ～48 ms，信号基波频率为50 Hz，谐波频率为150 Hz和250 Hz，幅值分别为 1.0052、0.3017 和0.15105;而在48 ～100 ms，信号基波频率约为50 Hz，间谐波频率为5 Hz，谐波频率为 200 Hz，幅值分别为 0.7075、0.1420 和0.1182。

由图4可以看出:STFT时频分析方法对频率定位并不准确，在信号的频率及幅值发生突变时会出现端点效应，无法准确估计突变位置。将本文算法与传统STFT时频分析实验结果进行误差分析比较，如表2所示，可知本文算法比STFT算法频率和幅值的估计相对误差小，精确度高。

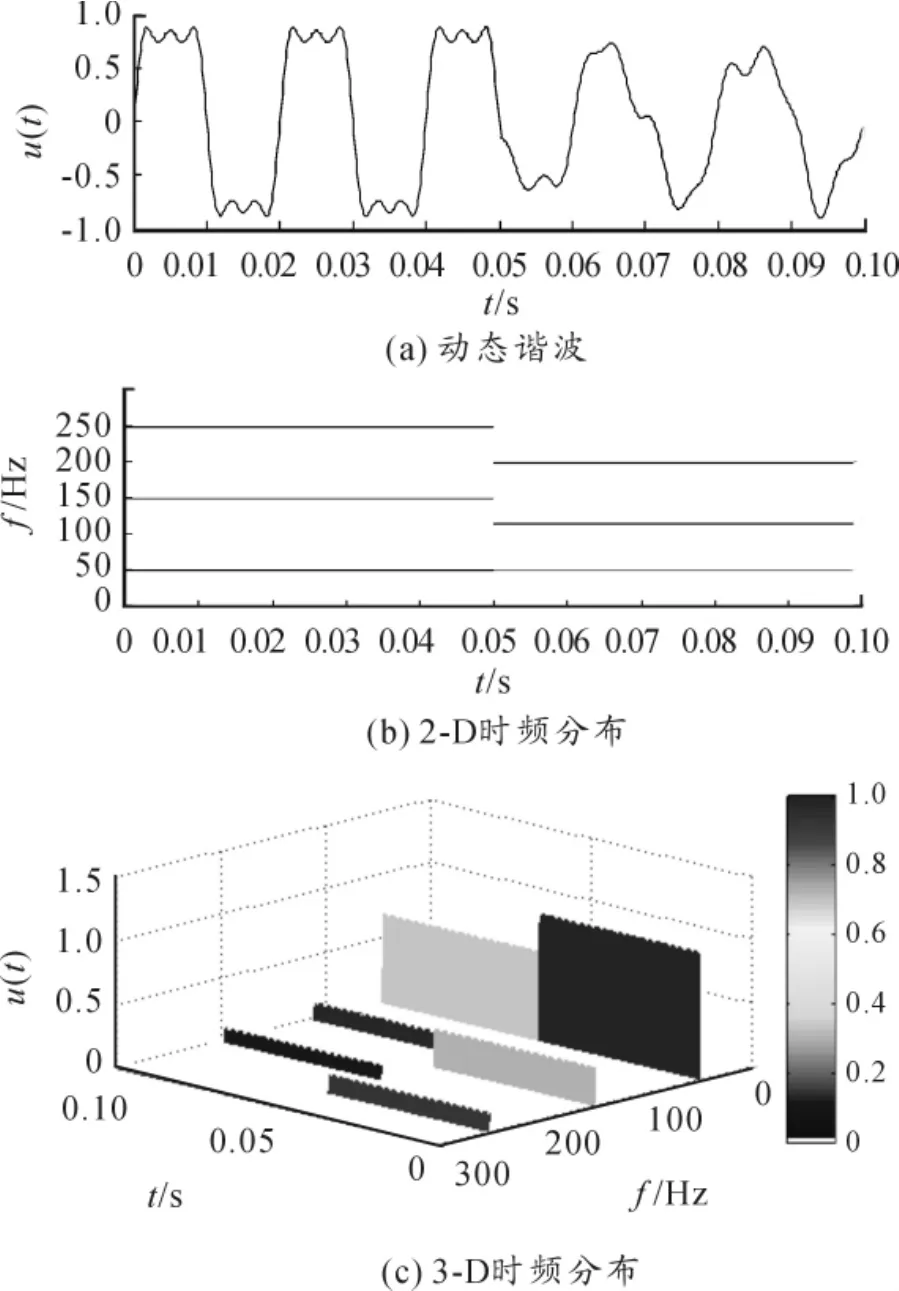
图3 动态谐波及检测结果

图4 动态谐波的STFT时频分析

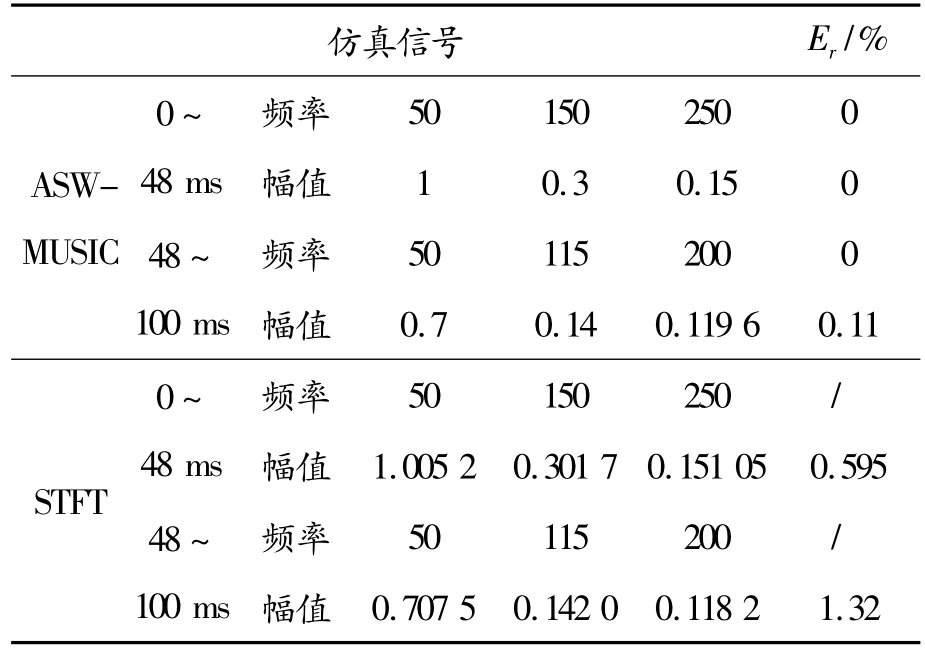
表2 ASW-TAM与STFT的比较

3 实测数据分析

为了进一步验证算法的可行性，对某钢铁企业6kV线路滤波线路进行监测，电压波形如图5(a)所示。

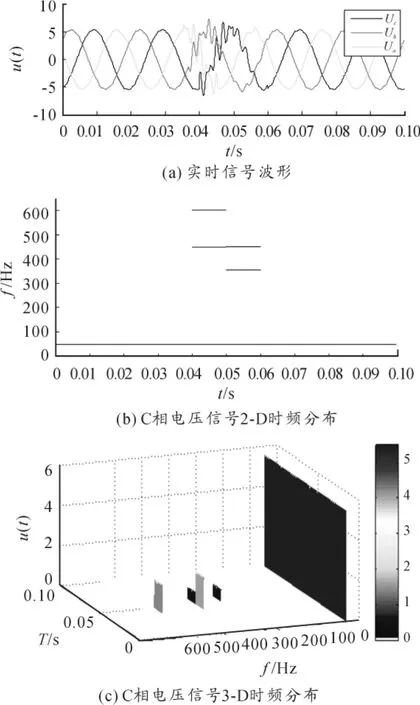
图5 电压短时振荡及检测结果

本文对C相电压进行处理，可得如图5(b)、图5(c)所示的时频分布结果，在0～39.975 ms基波电压频率为50.156 Hz，幅值为5.4768 kV。在39.975 ～49.996 ms内，信号频率值为 50.2095、607.6744、453.0687 Hz，幅值分别为 5.4206、1.318、1.5868 kV。在49.996 ～60 ms内，信号频率值为50.1570、360.0063、458.8343 Hz，幅值分别为 5.4881、0.5108、0.5297 kV。在 60 ～ 100 ms内，基波电压频率为 50.0851 Hz，幅值为5.40725 kV。因此，可得由于电容器投切导致在39.975～60 ms时间段内出现母线电压短时振荡。

4 结束语

ASW-TAM算法根据非平稳电能质量扰动信号特征对PQD信号进行分块，得到近似平稳信号的数据，再利用TAM算法对数据块进行参数估计，得到频率值和幅值，最后联合所有窗口的分析结果，便可给出时频分布结果。采用ASW-TAM算法对PQD信号进行时频分析，能有效地检测与分析电能质量干扰。提出的自适应滑窗思想，降低了传统滑窗TAM算法的计算量。仿真实验表明，ASW-TAM算法准确度较高，能克服传统时频分析方法存在的频率估计不准确以及端点效应、频谱泄露等问题。本文算法将非平稳信号通过时频分布图直观地表示出来，有利于对实际动态电能质量扰动信号进行定位、识别和检测。实际数据分析表明，该算法可以应用于对实际数据的处理，可以为电能质量暂态分析提供一种新的工具。

［1］李加升，戴瑜兴，柴世杰.基于预测机制的电能质量扰动检测方法研究［J］.电力系统保护与控制，2010，38(17):96－100.

［2］任明炜，孙玉坤，郑红平，等.电力系统谐波和基波无功检测改进方法［J］.江苏大学学报:自然科学版，2006，27(1):63 －66.

［3］覃思师，刘前进.基于STFT变换和DAGSVMs的电能质量扰动识别［J］.电力系统保护与控制，2011(17):83－86.

［4］储珺，马建伟.基于小波变换的电能量扰动信号的检测［J］.电力系统保护与控制，2009，37(5):34 －36.

［5］Herrraiz S，Heydt G T，O’Neill-Carrillo E.Power Quality Indices for Aperiodic Voltages and Currents［J］.IEEE Trans Power Del，2000，3:784 －790.

［6］王永良，陈辉，彭应宁，等.空间谱估计理论与算法［M］.北京:清华大学出版社，2004.

［7］蔡涛，段善旭，刘方锐.基于实值MUSIC算法的电力谐波分析［J］.电工技术学报，2009，24(12):149 －155.

［8］Kung S Y，Arun K S，Rao D V B.State space and SVD based approximation methods for the harmonic retrieval problem［J］.Opt Soc Amer，1983，73(12):1800 －1803.

［9］Kung S Y，Lo C K，Foka R.A toeplitz approximation approach to coherent source direction finding［J］.ICASSP，1986，11:193 －196.

［10］程志友，梁栋，韦穗，等.一种快速暂态电能质量扰动定位方法［J］.电力系统自动化，2007，31(27):73－76.

［11］孙金玮，刘昕，孙圣和.基于总体最小二乘法的多功能信号重构方法研究［J］.电子学报，2004，32(3):391－394.

［12］Silverstein S D，Zoltowski M D.The mathematical basis for element and fourier beamspace MUSIC and Root-MUSIC algorithms［J］.Digital siganal processing，1991，1(4):1－15.

［13］丁屹峰，程浩忠，吕干云，等.基于Prony算法的谐波和间谐波频谱估计［J］.电工技术学报，2005，20(10):94－97.