土层缺陷锚杆锚固特性与参数影响分析
段建,言志信,郭锐剑,谌文武,刘子振,3,任志华
(1. 兰州大学 西部灾害与环境力学教育部重点实验室,甘肃 兰州,730000;
2. 兰州大学 土木工程与力学学院,甘肃 兰州,730000;
3. 台州学院 建筑工程学院,浙江 台州,318000)
岩土锚固技术具有巧妙结构、简便工艺、经济造价、独特效果等突出优势,在工程各领域获得了广泛应用[1]。目前,就完整锚杆锚固特性研究方面,众多学者采用多种研究方法和手段取得了一系列研究成果,如Phillips等[2−6]采用相关理论来构建锚固体剪应力分布曲线函数;为了考虑岩土体弹塑性特性,Xiao等[7−9]分别建立岩土体弹塑性模型探讨锚固体锚固机理;Yang等[10]采用分离式模型建立了基于混凝土基质的锚杆二界面分布函数理论;战玉宝等[11−13]采用数值模拟技术分析锚固力学效应及影响因素;Delhomme等[14]通过试验与数值模拟对比分析研究了基于混凝土基质的锚杆拉拔与蠕变特性;ZHAO等[15]分析了基于混凝土基质的缺陷锚杆拉拔特性。然而,在工程施工中,锚杆锚固质量影响因素繁多,常常使得锚固体难以饱满,出现一些空腔缺陷,达不到设计要求,致使工程存在一定风险。而人们对有关缺陷锚杆锚固特性研究较少,因此,研究空腔对锚固系统的影响程度,为工程锚杆锚固质量后评价及修补决策提供理论支撑,均具有重要的理论和实践意义。本文作者基于界面黏滑本构模型假定,构建锚固体位移、轴力、锚固体周边剪应力微分表达式及土层缺陷锚杆锚固求解方法,探讨土层缺陷锚杆荷载传递特性,分析缺陷锚固系统参数影响规律。
1 土层缺陷锚杆锚固力学模型
1.1 锚杆锚固体与周边土体界面黏滑本构模型假定
为了考虑锚杆锚固体与周边土体界面黏滑特性,界面剪应力−剪切位移关系可采用分段线性函数模式来表征,如图1所示。第Ⅰ阶段为弹性阶段,锚杆锚固体−周边土体协同承载变形,界面剪应力与剪切位移呈比例关系变化;一旦锚杆锚固体−周边土体界面剪应力超过界面极限剪切强度,界面就会发生松动滑移,锚杆锚固体−周边土体界面产生相对滑动,其剪切变形可任意发展,此时界面之间仅存在残余剪切强度,如图1中的第Ⅱ阶段。
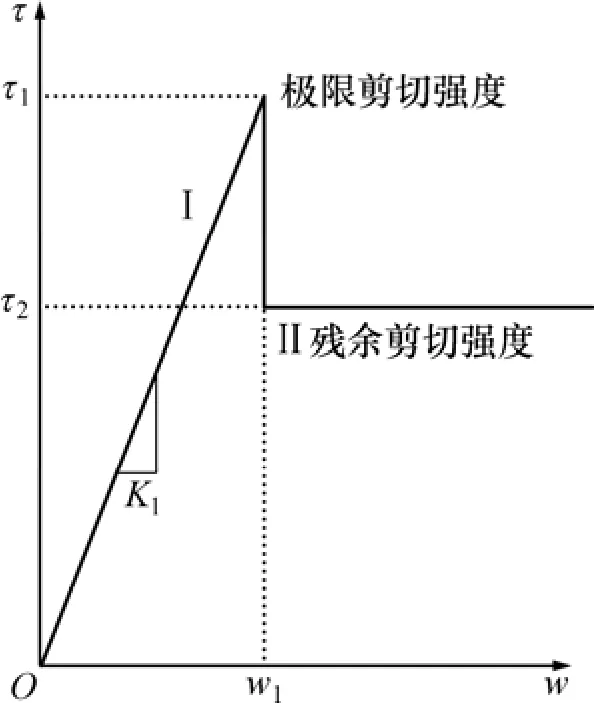
图1 界面本构模型Fig.1 Constitutive model of interface
相应的锚杆锚固体−周边土体界面黏滑本构关系数学表达式为:
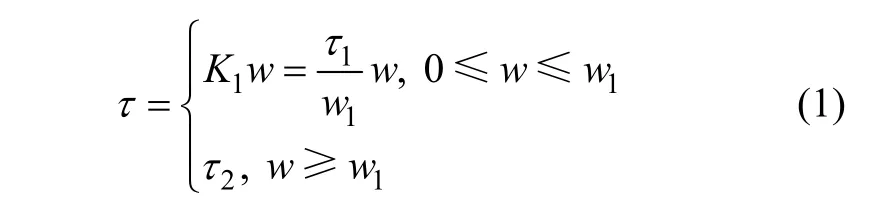
式中:τ为界面剪应力;K1为界面刚度系数;w为界面剪切位移;τ1为锚杆锚固段极限剪切强度;τ2为锚杆锚固段残余剪切强度;w1为锚杆锚固段极限剪切强度所对应的剪切位移。
1.2 锚固力学模型的构建
土层锚杆锚固系统一般由锚杆(索)、锚固剂及周边土体组成,可把锚杆(索)和锚固剂视为整体进行研究。因空腔缺陷的存在,土层缺陷锚杆锚固段被形成锚固−空腔交替组合的一种结构型式,共n段,其中偶数段为空腔,共(n−1)/2份,奇数段为锚固体,其对应(n+1)/2份,选取第i区段锚固段作为研究对象,如图2所示,根据锚固体轴力Pi(z)与应力应变之间关系可得:
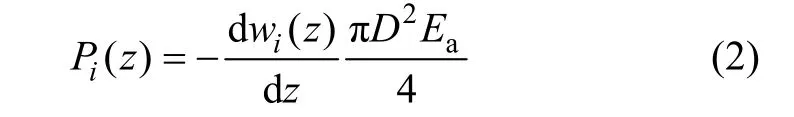
同时,由锚固体单元沿轴向方向力的平衡方程得:
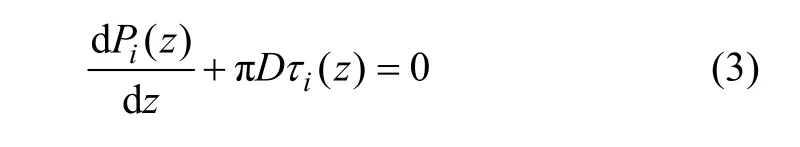
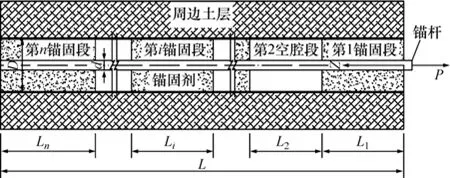
图2 计算模型Fig.2 Compute model
联立式(1)~(3)可获得第i区段锚固体轴向位移微分方程为:
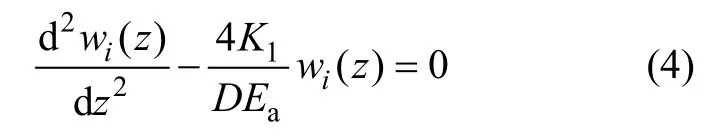
解为:
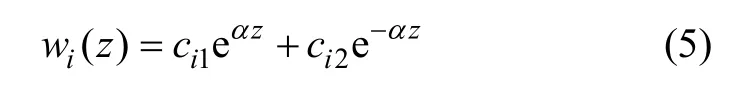
其中,ci1和ci2为待定常系数,可由该段边界条件确定。
对式(5)求微分,分别代入式(1)和(2)可获得第i段锚固体轴力及周边剪应力分布函数为:
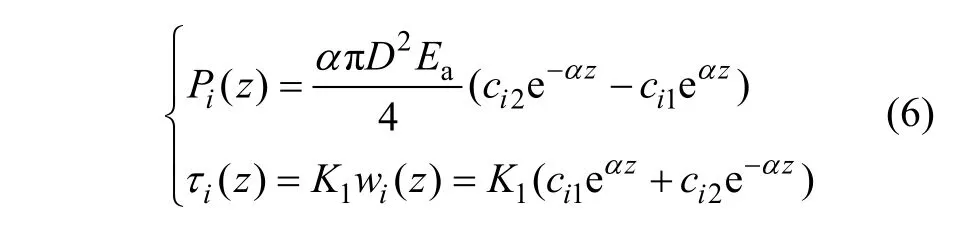
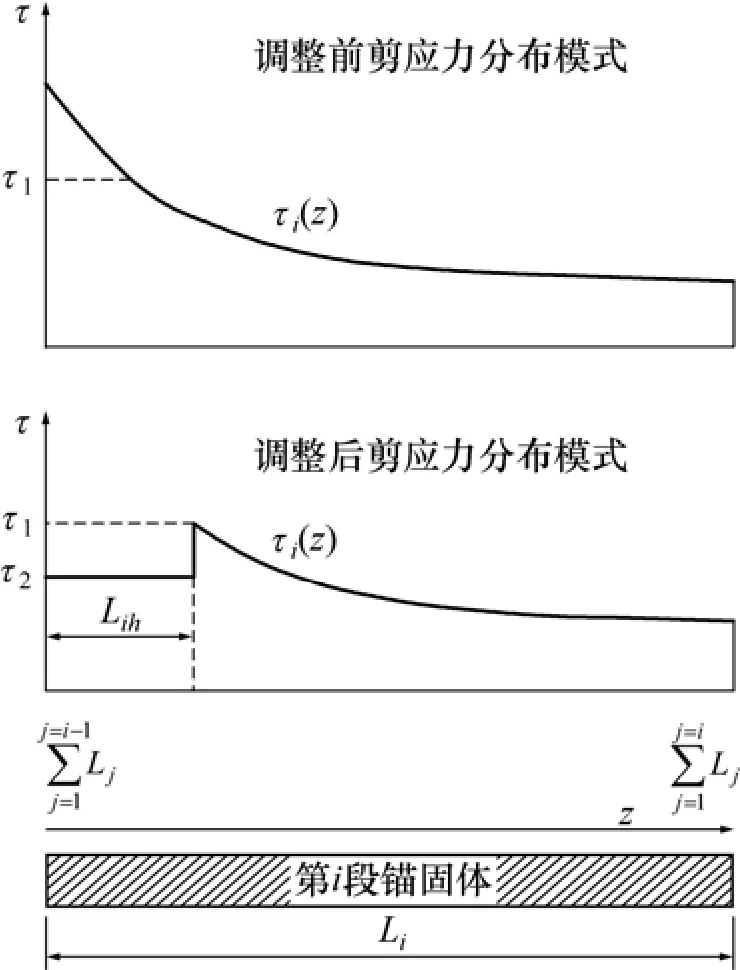
图3 锚固体剪应力调整模式Fig.3 Adjusted model of anchorage shear stress
对应第i−1空腔段锚杆位移、轴力及剪应力分布函数,可依据相邻第i锚固段力学特性及空腔特性确定:
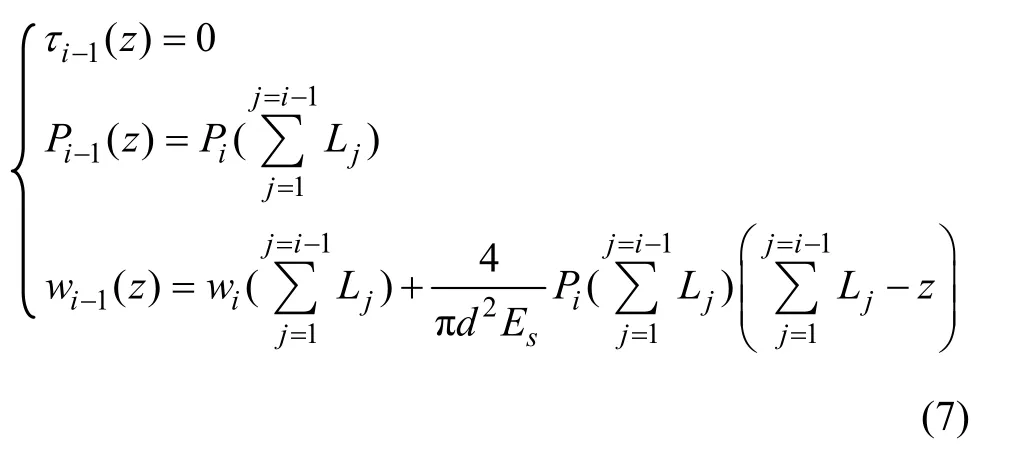
1.3 缺陷锚杆锚固问题的求解步骤
依据上述所建锚杆锚固段以及空腔段力学模型与解析解,对某一具体的缺陷锚杆锚固工程问题,可按下列步骤获得问题数值解。
第 1步:依据锚杆(索)设计长度及其空腔分布情况划分研究区段n段,分别建立各锚固段锚固体位移、剪应力及轴力数学方程,基于第1,n锚固段端头轴力边界条件和各锚固段相邻端头位移及轴力连续条件(如式(8)所示),即可确定各段待定常系数ci1,ci2,从而获得各段锚固体位移、轴力及周边剪应力分布数值弹性解。
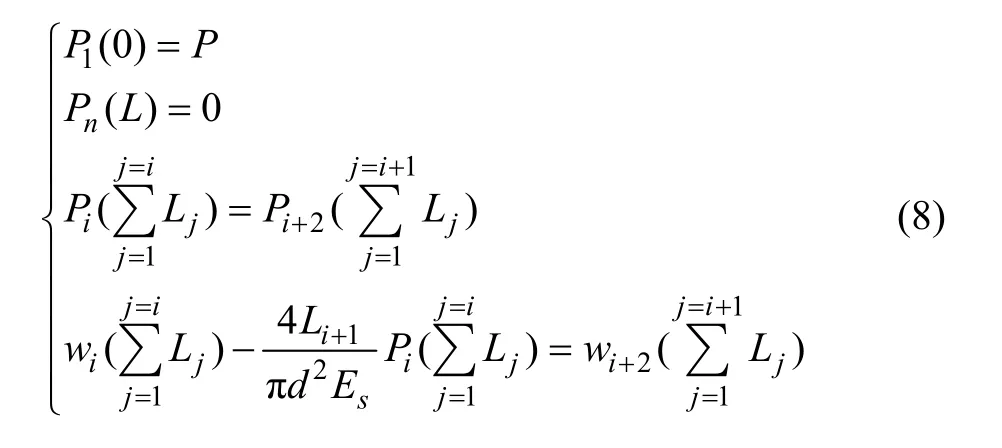
第 2步:依据锚杆锚固体剪应力衰减规律,τimax(z)=τ1max(z)=τ1(0),通过界面力学参数τ1与τ1(0)的比较来判断第1锚固段黏结−滑动状态:当τ1(0)≤τ1,说明各锚固段界面均处于黏结状态,剪应力不需调整分配,第1步所获锚固段数值解即为问题解;同时,由式(7)即可确定各空腔段解析解;若τ1(0)>τ1,即第1锚固段存在滑动区段,则对其按图3滑动段剪应力调整模式进行修正,此时,边界条件应修正为:
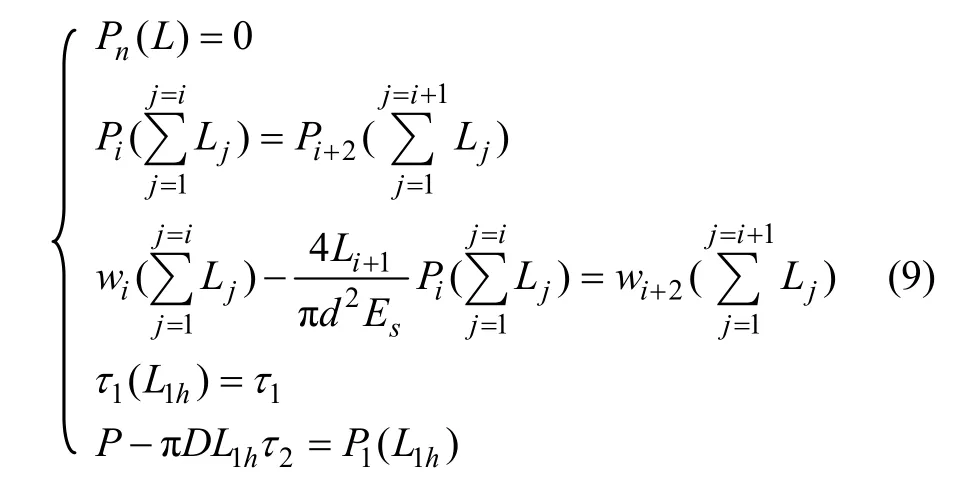
由式(9)和(7)分别可获得各锚固段和空腔段调整后的数值解,而对于滑动段(0≤z≤L1h≤L1),则可由式(10)确定:
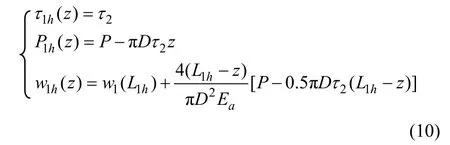
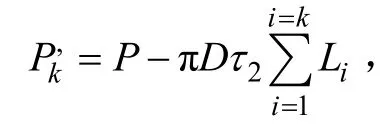
通过上述分析,土层缺陷锚杆锚固具体计算流程如图4所示。
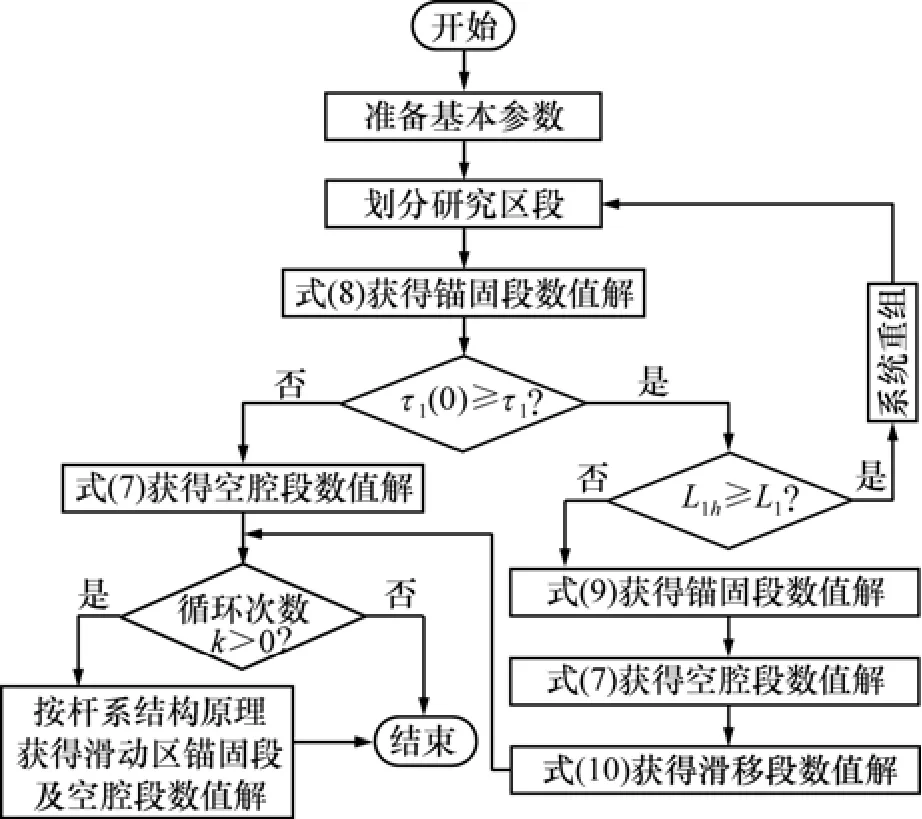
图4 计算流程Fig.4 Computational process
1.4 理论模型的验证
为了检验本文方法的合理性,工程选取湖南省株洲市天元区明峰银座商住楼基础工程,由钻探揭露该场地地层岩性为:第4系全新统素填土与耕土、第4系上更新统粉质黏土与砾砂及粉砂、白垩系泥质粉砂岩。因场地地下水位较高,该工程采用锚杆基础抗浮,共施工了抗浮锚杆 817根,采用φ28螺纹钢(三级钢)制作,孔径为130 mm,锚固剂采用M30水泥砂浆。对其中41根工程锚杆进行了抗拔试验(未做锚固体应力测试),为了验证本文方法的合理性,选取其中第420号锚杆荷载−位移检测数据进行对比分析。该锚杆全长为6.5 m,锚固质量完整,全长穿越圆砾碎石土(未穿透),根据其勘察成果,同时综合参考该地区同类土测试资料、岩土力学参数手册及相关工程经验,本工程地层物理力学参数见表1。
设计锚杆抗拔承载力特征值为128 kN,抗拔试验最大荷载根据规范及设计要求确定为 190 kN,采用QFZ100-20型张拉千斤顶与手摇高压油泵对锚杆进行施加拉拔力,试验采用分级加荷载法,前3级荷载按试验荷载的20%施加,以后按10%施加,分别对应荷载为38,76,114,133,152,171和190 kN,每级稳定后加下一级荷载,并记录对应的位移。
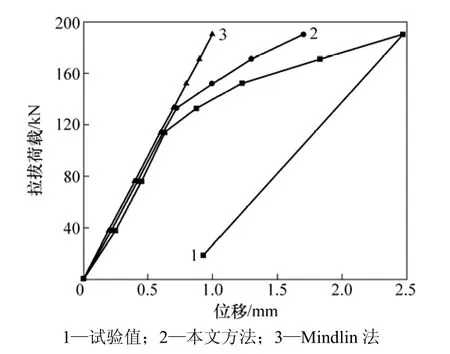
图5 420号锚杆载荷−位移曲线Fig.5 Load−displacement curve of No.420 anchor
锚杆拉拔试验获得的锚杆荷载-位移曲线及按本文方法及Mindlin法[3]计算的理论荷载−位移曲线如图5所示。从图5可见:当拉拔荷载比较小时,曲线均呈线性变化;随着荷载的增大,因Mindlin法是基于弹性理论原理构建的,荷载与位移间始终保持线性关系变化,而本文方法考虑了界面的黏滑特性,约在P=133 kN位置曲线开始向X位移轴偏转,变形速率增大,界面发生松动,与 Mindlin法相比,其结果更接近于实际。同时说明,从工程安全角度考虑,锚杆抗拔承载力特征值取128 kN是安全合理的;按照相关规范,工程锚杆拉拔至最大试验荷载190 kN,然后卸载至19 kN,可将试验卸载曲线延伸至X轴,发现锚杆变形并未归 0,产生了一定的塑性变形,这与本文方法计算结果一致。
2 土层缺陷锚杆锚固特性的参数影响分析
为了充分了解土层缺陷锚杆的荷载传递特性,基于一土层单空腔缺陷锚杆算例和本文方法分别从空腔大小、空腔位置以及拉拔荷载3方面开展缺陷锚杆锚固特性参数影响分析。算例基本资料如下:锚杆孔孔径D为110 mm,采用φ32螺纹钢筋,设计长度L=6 m,Es=200 GPa;锚固剂采用水泥砂浆,Em=20 GPa;周边土体力学参数K1=0.6 GPa/m,τ1=0.5 MPa,τ2=0.2 MPa;锚固体全长仅存在一处空腔,具体几何特征由其研究内容决定。
2.1 空腔尺寸的影响
假定空腔末端位置不变,z=4 m,拉拔荷载P=150 kN,设计4种缺陷长度方案:L2=0 m,L2=1 m,L2=2 m,L2=3 m,图6所示为空腔尺寸对锚杆锚固特性的影响结果。在相同荷载作用下,缺陷锚杆表现出与完整锚杆不一样的锚固特征,空腔的存在使得锚固段同一截面处剪切位移和剪应力均增大,空腔前段锚固段轴力减小,而后段则增大,总体上,空腔对缺陷锚杆前段锚固段锚固特性影响较大,而后段不是很明显;空腔段锚杆轴力及剪应力分布均为一水平平台,而剪切位移则为一下降直线形式,表现出明显的杆系结构受力特征。
同时,由图6还可得知:空腔尺寸对缺陷锚杆锚固特性影响也很大。随着空腔长度的增大,锚固段同一截面处剪切位移与剪应力均增大,轴力缺陷前段锚固段减小而后段增大;对应空腔段剪切位移下降幅度越大,轴力平台值也越大,而剪应力始终保持“0”水平平台特性。
2.2 空腔位置的影响
假定锚杆空腔缺陷长度L2=1 m,其他物理力学参数不变,考虑 1≤z≤2(位置 1),2≤z≤3(位置 2),3≤z≤4(位置3)3种空腔位置方案,分析P=150 kN作用下缺陷位置对锚杆锚固特性的影响,计算结果见图7。由图7可知:空腔位置越靠近拉拔顶端,前段锚固段同一位置处剪切位移和剪应力均越大,相应锚杆轴力下降幅度越大,而后段锚固段剪切位移、轴力及剪应力变化甚少,受影响程度小;对于锚杆空腔段,缺陷位置越靠近拉拔端,剪切位移斜率越小,轴力越大,剪应力则始终保持“0”水平平台特征。
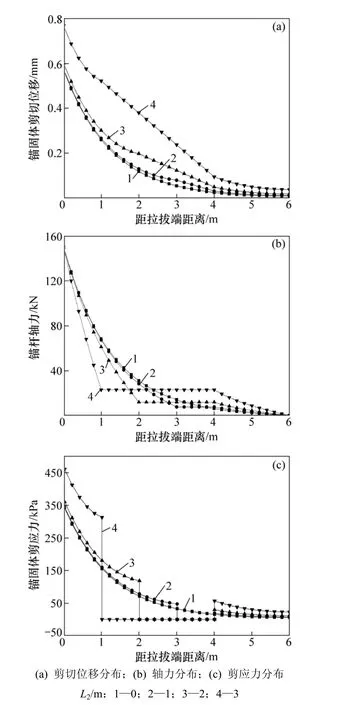
图6 不同空腔尺寸下缺陷锚杆锚固特征Fig.6 Anchorage characteristics of imperfect anchor under different imperfect dimensions
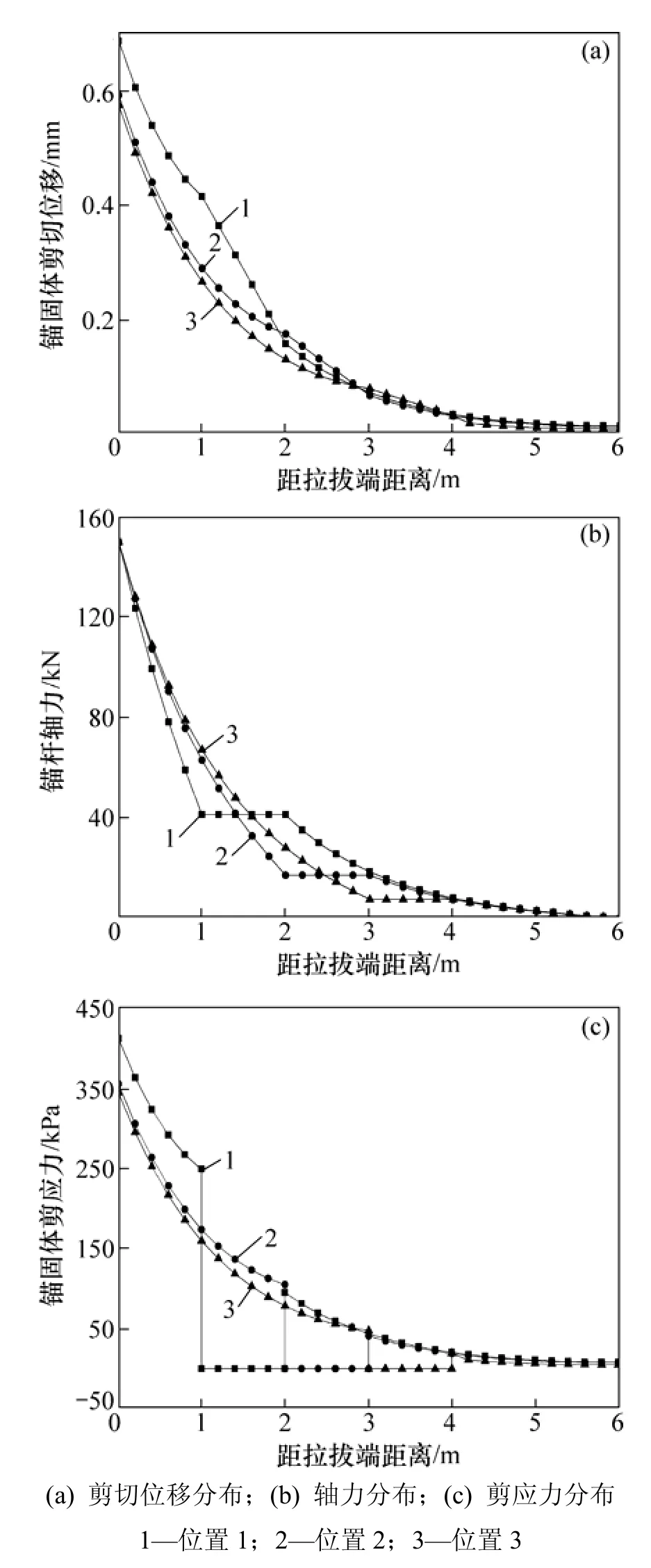
图7 不同空腔位置条件下缺陷锚杆锚固特征Fig.7 Anchorage characteristics of imperfect anchor under different imperfect locations
2.3 拉拔荷载的影响
假定锚杆空腔缺陷位于 3≤z≤4区段,其长度L2=1 m。根据上述计算方法,考察3种拉拔荷载P=100,200,240 kN作用下缺陷锚杆锚固段剪切位移、轴力及周边剪应力分布特征,如图8所示。从图8可见:当荷载较小时,随距锚固顶端距离的增大,锚固段剪切位移、轴力及剪应力均在衰减;同时,随着拉拔荷载的增大,锚固段同一位置处剪切位移、轴力及剪应力均在增加;当P=240 kN时,锚杆孔口处剪应力τ1(0)=0.551 MPa,已超过界面抗剪强度,剪应力需重新调整分配,通过计算获得锚杆松动滑移长度L1h=0.341 m,调整后相应滑动段上的剪应力转化为界面残余剪切强度,后续黏结段剪切位移、轴力及剪应力均比调整前有所上升,说明滑移松动后荷载进一步往锚杆里端传递,加剧里端锚固体损伤劣化;此外,随着荷载的增大,空腔段剪切位移下降直线对应斜率越小,剪切位移急剧下降,轴力及剪应力分布均为一水平平台,其中荷载越大,轴力也增大,而剪应力始终保持“0”水平平台特征。
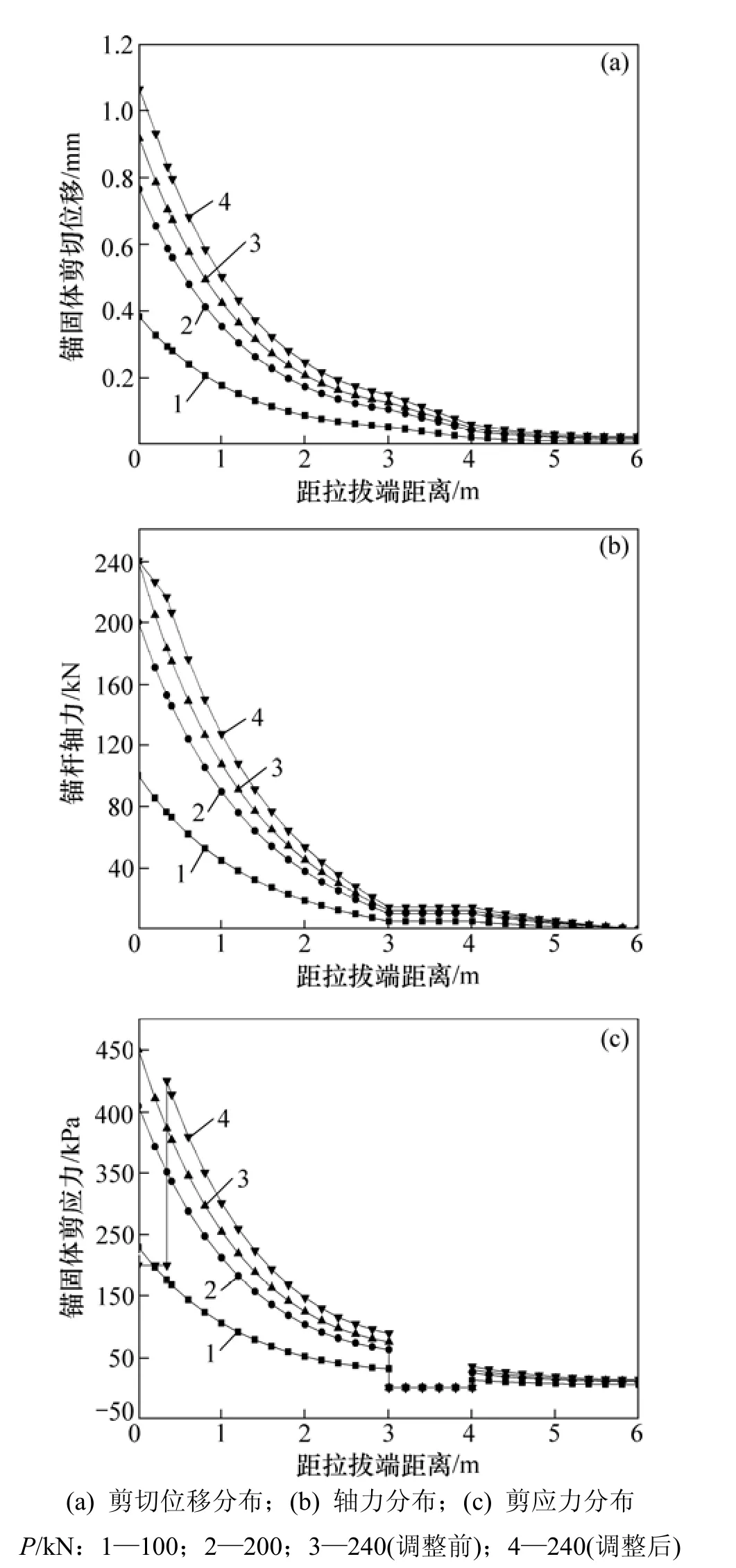
图8 不同荷载作用下缺陷锚杆锚固特征Fig.8 Anchorage characteristics of imperfect anchor under different loading
3 结论
(1) 依据界面黏滑本构模型假定,建立了锚杆锚固力学微分方程及其解析解,给出了土层缺陷锚杆锚固迭代计算方法与求解步骤,并结合已有的工程实例验证了本文方法的可行性。
(2) 缺陷锚杆具有与完整锚杆不一样的锚固特征,其剪切位移、轴力与剪应力分布函数均由连续多段函数形式组成,其中空腔段锚杆轴力及剪应力分布均具有水平平台特性。
(3) 界面黏滑特性导致剪应力重新调整分配,调整后锚杆锚固段剪切位移、轴力及剪应力均有所上升,荷载进一步往里端传递,加剧里端锚固段的损伤劣化。
(4) 空腔的存在对缺陷锚杆前段锚固段影响较大,而后段则影响较小。
[1] 程良奎. 岩土锚固的现状与发展[J]. 土木工程学报. 2001,34(3): 7−16.CHENG Liang-kui. Present status and development of ground anchorages[J]. China Civil Engineering Journal, 2001, 34(3):7−16.
[2] Phillips S H E. Factors affecting the design of anchorages in rock[R]. London: Cementation Research Ltd, 1970: 1−10.
[3] 尤春安. 全长粘结式锚杆的受力分析[J]. 岩石力学与工程学报, 2000, 19(3): 339−341.YOU Chun-an. Mechanical analysis on wholly grouted anchor[J].Chinese Journal of Rock Mechanics and Engineering, 2000,19(3): 339−341.
[4] 尤春安, 战玉宝. 预应力锚索锚固段应力分布规律及分析[J].岩石力学与工程学报, 2005, 24(6): 925−928.YOU Chun-an, ZHAN Yu-bao. Distributing characters and analysis of stresses in prestressed cable[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(6): 925−928.
[5] 蒋忠信. 拉力型锚索锚固段剪应力分布的高斯曲线模式[J].岩土工程学报, 2001, 23(6): 696−699.JIANG Zhong-xin. A gauss curve model on shear stress along anchoring section of anchoring rope of extensional force type[J].Chinese Journal of Geotechnical Engineering, 2001, 23(6):696−699.
[6] 张季如, 唐保付. 锚杆荷载传递机理分析的双曲函数模型[J].岩土工程学报, 2002, 24(2): 183−192.ZHANG Ji-ru, TANG Bao-fu. Hyperbolic function model to analyze load transfer mechanism on bolts[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(2): 183−192.
[7] XIAO Shu-jun, CHEN Chang-fu. Mechanical mechanism analysis of tension type anchor based on shear displacement method[J]. Journal of Central South University of Technology,2008(15): 106−111.
[8] 何思明, 李新坡. 预应力锚杆作用机制研究[J]. 岩石力学与工程学报, 2006, 25(9): 1876−1880.HE Si-ming, LI Xin-po. Study on mechanism of prestressed anchor bolt[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(9): 1876−1880.
[9] 何思明, 田金昌, 周建庭. 胶结式预应力锚索锚固段荷载传递特性研究[J]. 岩石力学与工程学报, 2006, 25(1): 117−121.HE Si-ming, TIAN Jin-chang, ZHOU Jian-ting. Study on load transfer of bond prestressed anchor rope[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(1): 117−121.
[10] Yang S T, Wu Z M, Hu X Z, et al. Theoretical analysis on pullout of anchor from anchor-mortar-concrete anchorage system[J].Eng Fract Mech, 2008, 75(5): 961−985.
[11] 战玉宝, 毕宣可, 尤春安. 预应力锚索锚固段应力分布影响因素分析[J]. 土木工程学报, 2007, 40(6): 49−53.ZHAN Yu-bao, BI Xuan-ke, YOU Chun-an. Analysis of factors influencing the stress distribution in prestressed cables[J]. China Civil Engineering Journal, 2007, 40(6): 49−53.
[12] 江文武, 徐国元, 马长年. FLAC-3D 的锚杆拉拔数值模拟试验[J]. 哈尔滨工业大学学报, 2009, 41(10): 129−133.JIANG Wen-wu, XU Guo-yuan, MA Chang-nian. Numerical simulation on pull-tests of a cable by FLAC-3D[J]. Journal of Harbin Institute of Technology, 2009, 41(10): 129−133.
[13] 庞有师, 刘汉龙, 陈育民. 可回收式锚杆拉拔试验的数值模拟与影响因素分析[J]. 解放军理工大学学报: 自然科学版,2009, 10(2): 170−174.PANG You-shi, LIU Han-long, CHEN Yu-min. Numerical simulation of removable anchor pullout test and influence factors[J]. Journal of PLA University of Science and Technology:Natural Science Edition, 2009, 10(2): 170−174.
[14] Delhomme F, Debicki G. Numerical modeling of anchor bolts under pullout and relaxation tests[J]. Constr Build Mater, 2010,24(7): 1232−1238.
[15] ZHAO Yi-ming, YANG Mi-jia. Pull-out behavior of an imperfectly bonded anchor system[J]. International Journal of Rock Mechanics & Mining Sciences. 2011 (48): 469−475.

