基于物理规划的路径诱导方法

龙琼，胡列格，张蕾，喻杰

(1. 湖南城市学院 土木工程学院，湖南 益阳，413000；2. 长沙理工大学 交通运输工程学院，湖南 长沙，410004)

路径诱导系统(Route guidance system)是智能交通系统的核心组成部分之一[1−2]。路径诱导系统通过诱导信息来改变出行者的出行行为，降低出行者对未知交通状态的焦虑，为驾驶员找到从当前位置到目的地的最优行驶路径。但驾驶员对于最优路径的理解和要求因人而异，也会随时间和旅行目的不同而变化，因此，最优路径的标准不是唯一和固定不变的。在当前的大多数路径诱导系统中，其优化目标一般表示为出行时间最短或出行距离最短[3−4]，而没有深入考虑驾驶员的性格特点、交通状况、出行目的等因素，所以，其“最优”的含义是狭隘的，所获得的最优解也不一定能够满足驾驶员的期望[5−6]。因此，在路径诱导过程中，引入驾驶员的个人偏好，体现路径诱导系统的个性化特点，协调好各种选择标准, 提出一种有效的最优路径诱导方法有重要意义。很多研究者尝试利用模糊逻辑、人工智能、近似推理等理论来解决该问题，如Pang等[7]提出了一种基于模糊神经网络的路径选择方法。该方法利用模糊神经网络表达影响路径选择的各种因素的相关关系并最终根据驾驶员的偏好给出所有可行路径的优劣排序。但该方法需经过多次运行训练后才能比较有效，改变偏好信息的当次无法由系统提供满足特殊要求的最优路径。孙燕等[5]基于层次分析法和灰色评价理论建立了一种根据驾驶员的偏好自适应选择最优路径的方法，能够在可行路径集中搜索满足驾驶员个人偏好的最优路径，但并没有将这种路径选择方法引入路径诱导过程，仅对可行路径进行个性化选择，因而存在一定的局限性。为此，本文作者针对智能交通系统中路径诱导问题的特点，将驾驶员个人偏好量化为偏好函数，引入路径诱导过程中，提出一种基于物理规划的路径诱导方法。该方法充分考虑了驾驶员的个性化需求，能够满足不同驾驶员的个性偏好，自适应地为驾驶员提供期望的最优路径。

1 物理规划方法概述

1.1 基本思路

物理规划是Messac于1995年提出的一种处理多目标优化设计问题的有效方法。该方法将整个设计过程置于一个更加灵活、自然的框架中，以减轻计算负担，便于实际应用。该方法能够从本质上把握使用者的偏好，是处理多目标优化问题的新框架。其基本思路是：引入偏好函数，将不同物理意义的各种设计目标转换为具有相同数量级的无量纲的满意度目标。通过对偏好函数的优化，寻求对综合目标满意度最优的设计点作为问题的最优解。因此，建立偏好函数是物理规划问题的关键，它反映设计者对各设计目标的偏好程度[7−10]。

1.2 偏好函数的数学描述

偏好函数是设计指标的函数，记第i个设计指标xi的偏好函数为ui(xi)。物理规划中对设计指标的偏好分为以下4种类型：(1) Class1，设计指标越小越好；(2) Class2，设计指标越大越好；(3) Class 3，设计指标趋于某值最好；(4) Class4，设计指标在某取值范围最好。偏好函数又分为软、硬(S和H) 2种类型。软型偏好函数是指偏好函数值在可行域内随设计指标变化，体现对设计指标不同取值的不同偏好程度。对于硬型偏好函数，当设计指标在可行域内时函数值均取最小，表示只要设计指标可行即可。因此，偏好函数具有图1所示的8种基本类型。在工程优化问题中，一般采用软偏好函数描述设计目标，硬偏好函数描述约束条件。

为更加具体、灵活地体现设计者的偏好，物理规划将软偏好函数的设计目标分为几个连续的不同满意程度的区间。以Class1-S型为例，对某一设计目标进行区间划分：

(1) 很期望域(xi≤xi1)，设计者可以接受的范围，且对该范围内的目标值很期望；

(2) 期望域(xi1≤xi≤xi2)，设计者期望的可接受范围；(3) 可忍受域(xi2≤xi≤xi3)，设计者可接受的范围；(4) 不期望域(xi3≤xi≤xi4)，设计者可接受但不期望的范围；

(5) 很不期望域(xi4≤xi≤xi5)，目标在该区间可接受但很不期望；

(6) 不可接受域(xi5≤xi)，目标在该范围内不可接受。

其中：xi1～xi5是设计者根据其偏好给定的第i个设计目标的区间端点值，如图2所示。

1.3 物理规划问题的数学模型

文献[11]取各设计目标的偏好函数平均值的常用对数作为综合偏好函数，即

其中：n为偏好函数的个数。可见，物理规划问题可以表述为：综合选择合适的偏好函数变量xi(i=1，2，…，n)，使得综合偏好函数值J最小，即J→min。在通常情况下，各偏好函数变量xi之间是相互耦合的，这将给规划过程带来了难度。

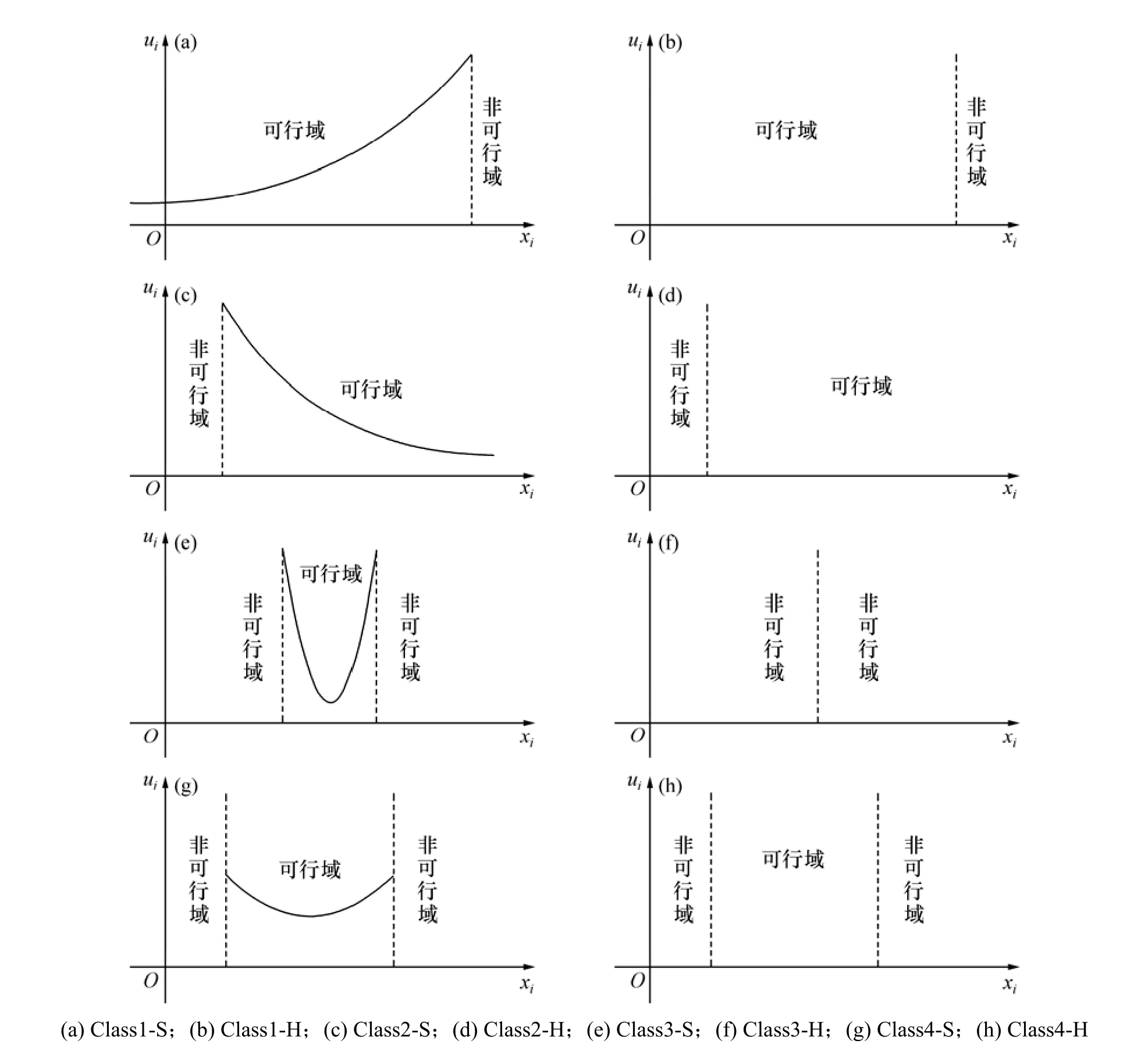
图1 偏好函数的基本类型Fig.1 Fundamental type of Preference functions

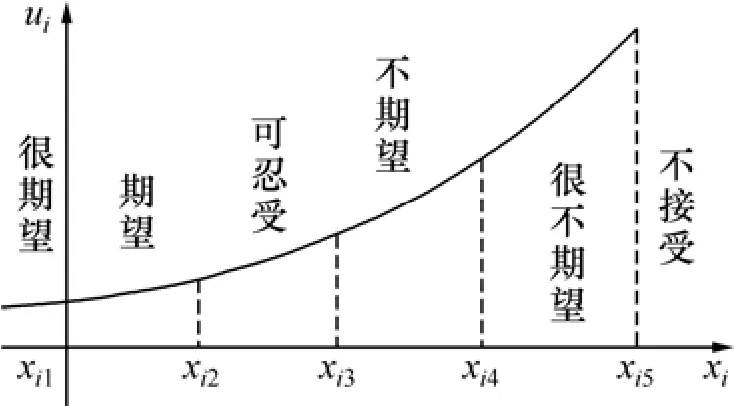
图2 偏好函数的区间划分示意图Fig.2 Interval differentiate schemes of preference functions

2 路径诱导模型构建

式(1)建立了1个物理规划问题的通用数学模型。从式(1)可以看出：该模型对各种与路径选择有关的因素(偏好函数)同等看待，这将影响路径诱导的灵活性，也难以反映驾驶员的个性化特点。事实上，不同驾驶员对于每个偏好函数的看重程度并不一定相同，在不同的情况下(如不同出现目的、不同天气、不同时间)，即使是同一驾驶员，对每个偏好函数的看重程度也会存在差异。因此，在路径诱导问题中，为了体现驾驶员的个性化偏好，有必要在综合偏好函数中引入偏好系数λi。此外，考虑到常用对数是单调递增函数，将其引入综合偏好并无实质意义，所以，本文设计路径诱导的优化模型为其中：ui(j)表示在所经历道路序列中的第j条道路关于评价指标xi的偏好值；1/m是为了与路径代价保持一致性而引入的加权因子。在一般情况下，设计评价指标的偏好函数仅为Class1-S型和Class2-S型，故

或

从式(2)可以看出：考虑驾驶员个人偏好的最优路径模型与其各项分类指标xi、偏好函数fi以及偏好系数λi紧密相关。因此，构建能够反映驾驶员性格偏好的路径诱导模型的关键在于：路径评价指标体系的构建、诱导偏好函数的数学表达以及偏好系数的设计这3个方面。

2.1 路径评价指标体系的构建

评价1条路径的优劣，仅仅考虑其行驶距离或者行驶时间是不够的，还应该考虑可行路径的特点、驾驶员的性格特点、特定出行的性质(如目的、预算)以及驾驶环境(如天气、白天晚上)等因素，因此，路径评价具有一定的主观性，因人而异。本文综合考虑驾驶员的个性化需求，参照文献[4]，构建路径评价指标体系如下的评价指标体系：

其中：x1为行驶距离，行驶距离越短，偏好函数值越小，期望度越高；x2为行驶速度，交通流诱导系统控制中心预先根据当前交通状况估计每段道路上的平均行驶速度，行驶速度越高，偏好函数值越小，期望度越高；x3为拥挤程度，主要考虑道路上的车辆密度、排队长度、红灯等待时间等，拥挤程度越低，偏好函数值越小，期望度越高；x4为通行费用，针对高速公路、国道等收费道路。通行费用越少，偏好函数值越小，期望度越高；x5为行驶难度，主要考虑道路宽度、车道数、行人及非机动车数量等。行驶难度越小，偏好函数值越小，期望度越高；x6为沿途景观，进行长途旅行时，沿途景观有时也是1个需要考虑的因素。沿途景观越好，偏好函数值越小，期望度越高。

2.2 偏好函数的数学表达

偏好函数取值没有严格限定，只需能反映出在不同偏好区间中设计者对目标值的满意度即可[5]。本文设计偏好函数曲线为自然对数曲线(以Class1-S为例)，表达式如下：其中：e为自然对数的底数。

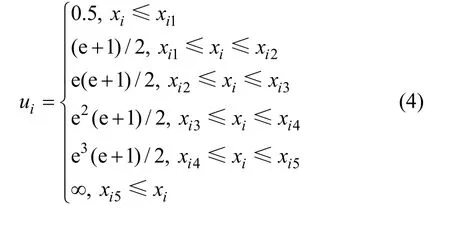
2.3 偏好系数设计

对于同一路径评价指标，每个驾驶员对其注重程度不一定一致。例如，当急于赶时间时，驾驶员通常注重的是行驶距离和行驶速度；当驾驶技术比较生疏时，驾驶员通常需要考虑道路的行驶难度；外出旅行时，驾驶员通常会选择具有较好沿途景观道路。因此，为了体现驾驶员的个性化需求，有必要设计对不同路径评价指标的偏好系数。

按照偏好程度逐渐下降的顺序，本文将偏好系数分为6个等级：“极重要”、“很重要”、“重要”、“稍重要”、“不重要”、“不关心”，如表1所示。

将表格中“不关心”的偏好指标对应的偏好系数置0，其他偏好系数按照主观赋权法设置相应的值，即

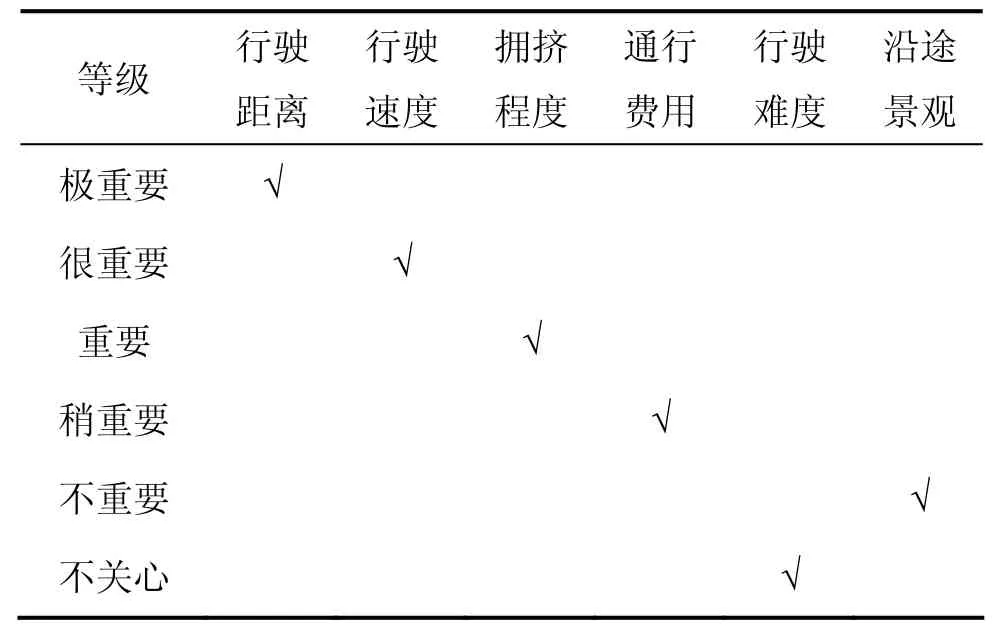
表1 路径选择因素的偏好程度界面Table 1 Interface of preference of path selection factors

3 路径诱导方法

3.1 基本思路

基于A*算法[11]进行路径搜索，其基本思路如下：在构建交通路网数据库的基础上，基于前面构建的路径诱导模型，设计合适的代价函数，从驾驶起点出发，基于A*算法在交通路网中依次扩展相应的路径节点，直到扩展至目标节点结束，从而从目标节点回溯至起点，最终得到一条能够反映驾驶员个人偏好的最优路径。

3.2 路网数据库构建

当考虑用户偏好时，路网数据库的构建不仅要包含交通路网中每条道路的长度，而且要考虑每条可行道路上的行驶速度、拥挤程度、通行费用、行车难度、沿途景观等因素，所以，构建对每条道路描述的数据结构如下：

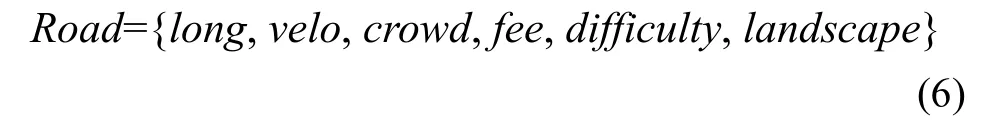
式中：long为道路长度，velo,crowd,fee,difficulty和landscape依次为对该条道路上的行驶速度、拥挤程度、通行费用、行车难度、沿途景观的评价。需说明的是：对于驾驶员而言，其关心的是行驶总路程，所以，对于单条道路的长度评价是没有意义的。因此，在数据库构建阶段，只需保留长度，而无需对其进行数值上的评价。为了避免主观标准的不同而导致路径评价的随意性，在此采用统计法对这些参数进行评判，从而得到一个较客观的评价数值。

以对某条道路上的行驶速度评价为例，首先，根据经验确定速度评价的区间划分参数，从小到大依次为v1，v2，v3，v4和v5；然后，交通流诱导系统控制中心实时测算该条道路上的平均时速；最后，参照式(4)，确定该条道路上行驶速度的数值评价(偏好函数值)：

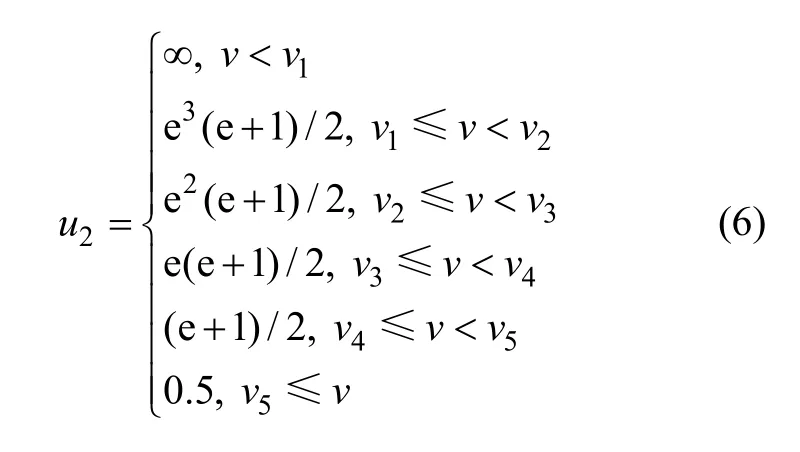
其他参数的数值评价方法与行驶速度评价类似。将数值评价结果由交通流诱导系统控制中心统一管理，从而构建了交通路网数据库，为后继的路径诱导过程提供数据支持。

3.3 代价函数

从路径诱导模型(式(2))可以看出：考虑驾驶员个性偏好的路径诱导是一个多目标优化问题。为了提高搜索效率，保证搜索的最优路径能够满足驾驶员的个性偏好，同时考虑到驾驶员关心的是行驶总路程，对单条道路长度进行评价是没有意义的，而其他评价指标均是针对单条道路进行评价的，为此，本文将代价函数分为2部分，即针对行驶总路程评价的代价函数和针对其他评价指标的综合代价函数。分别基于 A*算法的思想进行路径搜索[12]，代价函数如下：

其中：f1(k)为针对行驶总路程x1的评价代价函数，

式中：g1(k)为驾驶员从起始位置到当前路网节点的实际路径代价；h1(k)为从当前路网节点到达终点位置的启发路径代价，可取h1(k)为当前路网节点至终点的直线距离；u1(·)为路径长度评价函数；f2(k)为针对其他评价指标x2～5的综合代价函数，gi(k)为驾驶员从起始位置到当前路网节点的针对评价参数xi的实际评价代价；hi(k)为从当前路网节点到达终点位置的启发评价代价。由于在通常情况下，hi(k)难以预估，为了研究方便，本文仅以路径代价进行启发搜索，即取：

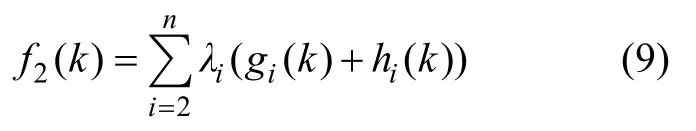
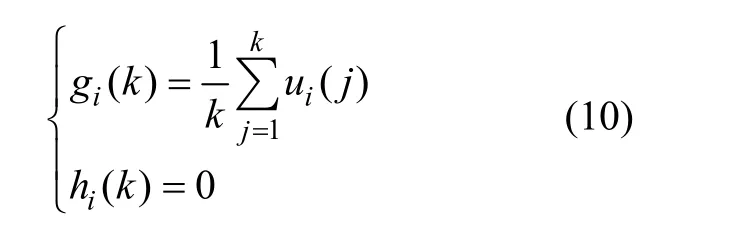
3.4 算法描述

基于物理规划的路径诱导算法具体步骤如下。

Step 1：初始化。确定行驶起点和目的点，载入相应的交通路网，根据当前的交通状况，智能交通系统自动对每条道路进行数值评价，确定其偏好函数值(注：对于通行费用、行车难度、沿途景观等，可以在交通路网数据库构建的初期进行评价；而对于拥堵行驶速度、拥挤程度等，则需要实时进行更新)。

Step 2：个性化选择。驾驶员根据在终端系统中输入个人偏好，如表1所示。

Step 3：最优路径搜索。根据起点和目的点坐标，采用 A*算法在交通路网中搜索满意度最高的最优路径。

1) 生成1个只包含起始节点的搜索图G，把起始节点插入OPEN表中，将CLOSED表置空。

2) 若OPEN表为空，则失败退出。

3) 选择OPEN表中的第1个节点，把它从OPEN表中移入CLOSED表中。

4) 若当前节点为目标节点，则将目标节点的父节点指针指向当前节点，路径搜索过程结束。从目标点开始向上回溯直到起始位置，得到从起始到目标的最小代价路径。

5) 基于交通路网图，扩展当前路径节点。生成其后继节点集M，注意当前节点的祖先不在M中，在G中安置M的成员，使之成为当前节点的后继。

6) 从M的每一个不在G中的成员建立一个指向当前节点的指针。把M的这些成员加到OPEN中，对M的每一个已在OPEN中或CLOSED中的成员m。若到目前位置找到的到达m的最好路径通过当前节点，就把它的指针指向当前节点。对于已在CLOSED中的M的每一个成员，重新定性它在G中的每一个后继，以使他们顺着到目前为止发现的最好路径指向它们的祖先。

7) 递增f，重排OPEN表。

8) 返回步骤3。

Step 4：输出最优路径。

4 仿真算例

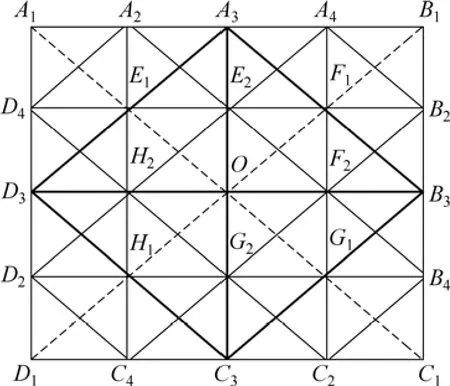
图3 交通路网示意图Fig.3 Traffic network

为了验证本文方法的有效性，在如图3所示的给定的城市交通路网图中进行路径诱导仿真。图3中：O为城市中心；E1—F1—G1—H1—E1包含的区域为“城内”，其他区域为“城外”；A1—B1—C1—D1—A1为绕城高速；A3—B3—C3—D3—A3，A3—C3和B3—D3为城区主道；A1—C1和B1—D1为正在维修中的街道；其他为一般的城市街道。交通路网中每一单元网格的边长均为1(如A1—D4)，则其对角边长为(如A1—E1)。

对于总路程的评价，取总路程与始末两点直线距离的比值μ作为评价参数。区间划分为： )2.1,1[ ，对应的平均值依次为：0.5，(e+1)/2，e(e+1)/2，e2(e+1)/2，e3(e+1)/2和∞。其他相关参数设置如表2所示。

假设驾驶员从A1出发，要抵达终点C1，求在不同需求情况下的最优路径。

(1) 情况1：驾驶员有紧急事情，希望以很短的时间抵达终点C1，但驾驶员处于实习期间，驾驶技术不太熟练，希望道路上车流量较小，路况较好。该驾驶员将行驶距离和行驶速度设置为“极重要”，拥挤程度和行车难度设为“重要”，其他指标设置为“不关心”。按照第3节的方法和步骤进行路径规划，得到最优结果为(图4所示)。

或者

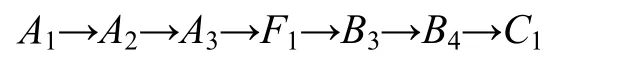
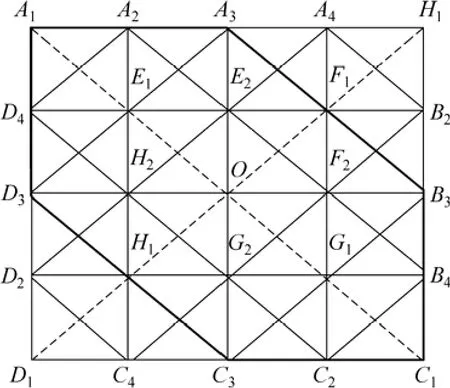
图4 优化路径示意图1Fig.4 Optimization path of traffic network

从搜索结果可以看出：基于物理规划的搜索结果行驶行驶距离不太大，行驶速度整体较高，因而能够以很短的时间抵达终点；同时，所选择的道路拥挤程度较低，行车难度较小，符合驾驶员的主观期望。

(2) 情况2：驾驶员外出游玩，希望在不产生较大费用的情况下好好体验沿途的风景，不大注重行驶距离和行驶速度；同时，该驾驶员技术熟练，对交通状况和路况宽窄情况不大在乎。该驾驶员将行驶距离和行驶速度设置为“稍重要”，拥挤程度和行驶难度设置为“稍重要”，通行费用设置为“重要”，沿途景观设置为“极重要”。

通过规划，得到最优结果为：

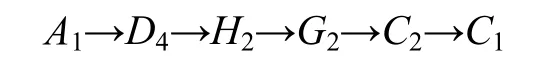
或者

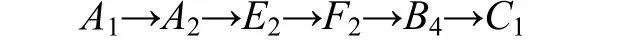
该搜索结果体现了低通行费用和好沿途景观的特点，较好反映了驾驶员的个性化偏好。

以上2个仿真算例表明：由于偏好函数的引入，基于物理规划的路径诱导方法符合驾驶员进行路径选择的决策行为特征，能够满足不同驾驶员的出行需求。

表2 交通路网相关参数设置Table 2 Traffic network related parameters settings

5 结论

(1) 基于物理规划理论，引入偏好函数，提出了一种能够反映驾驶员偏好的路径诱导方法。仿真算例表明，路径诱导结果符合驾驶员的个性化选择。

(2) 该方法能够有效协调好各种路径选择标准，体现了路径诱导系统的个性化特点，能够满足不同驾驶员的个性偏好，自适应地为驾驶员提供期望的最优路径。

(3) 该方法克服了以往规划方法目标单一的缺点，为智能交通系统的研究提供了一定的借鉴意义；需说明的是：该方法将路网交通信息进行量化，在此基础上进行最优路径的搜索，该方法实际上是一种静态的路径诱导方法。而事实上，路网交通信息是实时变化的，因此，有必要基于动态的路网环境对个性化路径诱导策略进行研究。

[1] 杨兆升. 城市交通流诱导系统理论与模型[M]. 北京: 人民交通出版社, 2000: 14−29.YANG Zhao-shen. The urban traffic flow guidance system theory and model[M]. Beijing: China Communications Press,2000: 14−29.

[2] 李威武, 王慧, 钱积新. 智能交通系统中路径诱导算法研究进展[J]. 浙江大学学报: 工学版, 2005, 39(6): 819−825.LI Wei-wu, WANG Hui, QIAN Ji-xin. New trends in route guidance algorithm research of intelligent transportation system[J]. Journal of Zhejiang University: Engineering Science,2005, 39(6): 819−825.

[3] WANG Hui. Transportation shortest path search area model[R].ProQuest Information and Learning Company, 2003: 119−121.

[4] Younes H, Patrice M S N. A strategic model for dynamic traffic assignment[J]. Networks and Spatial Economics, 2004, 4(2):291−315.

[5] 孙燕, 陈森发, 黄鹍. 基于灰色评价理论的自适应最优路径选择[J]. 中国公路学报, 2003, 16(4): 87−90.SUN Yan, CHEN Sen-fa, HUANG Kun. Adaptive optimal route selection based on gray evaluation theory[J]. China Journal of Highway and Transport, 2003, 16(4): 87−90.

[6] Jeffer L A, Goutam S P, Vikram M, et al. A multi-agent approach to cooperative traffic management and route guidance[J]. TransPortion Reasearch Part B, 2005, 39(4):297−318.

[7] Pang K H, Cran T. Adaptive route selection for dynamic route guidance system based on fuzzy neural approaches[J]. IEEE Transactions on Vehicular Technology, 1999, 48(6): 2028−2041.[8] McAllister C D, Simpson T W, Kemper L, et al. Robust multiobjective optimization through collaborative optimization and linear physical programming[C]//10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference.Albany, New York, 2004: 1−16.

[9] Achille M, CHEN Xuan. Visualizing the optimization process in real-time using physical programming[J]. Eengineering Optimization, 2000, 32(6): 721−747.

[10] 雍恩米, 陈磊, 唐国金. 基于物理规划的高超声速飞行器滑翔式再入轨迹优化[J]. 航空学报，2008, 29(5): 1091−1097.YONG En-mi, CHEN Lei, TANG Guo-jin. Trajectory optimization of hypersonic gliding reentry vehicle based on the physical programming[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(5): 1091−1097.

[11] 龙科军, 王赛政, 肖向良. 面向驾驶员特性的路径规划算法[J]. 计算机工程, 2011, 37(5): 264−265.LONG Ke-jun, WANG Sai-zheng, XIAO Xiang-liang. Driver character-oriented algorithm for route planning[J]. Computer Engineering, 2011, 37(5): 264−265.