城市轻轨钢−混凝土组合梁施工阶段的受力性能

(同济大学 土木工程学院，上海，200092)

城市轨道交通主要包括轻轨和地铁2种。地铁系统的建设周期较长，且造价较高，这使得轻轨越来越受到重视。目前，城市轻轨以高架无碴轨道为主，无法利用道碴来调节轨道高程，从而使其在运营阶段用于线路平顺性的变形调整量很少，且过大的变形还可能导致钢轨扣件破坏失效，降低轨道的稳定性，影响列车的安全运营[1]。因此，为了满足城市轻轨轨道梁对变形的高精度要求，保证行车的舒适性和安全性，对其在正常运营阶段和施工阶段的受力性能进行研究是十分必要的。城市轻轨中常用的轨道梁型式有预应力混凝土梁和钢−混凝土组合梁 2种。目前，人们针对预应力混凝土轨道梁开展了一系列的研究[1−2]。Xue等[3]以工业厂房钢−混凝土组合梁为原型，对1根非预应力组合梁和2根预应力组合梁进行为期1 a的长期荷载试验。樊健生等[4]通过4根非预应力钢−混凝土组合梁为期1 a的长期荷载试验，重点研究了变形随时间的变化规律。Bradford等[5]通过 4根非预应力简支组合梁为期240 d的长期试验，重点研究了栓钉间距和工作荷载对其受力性能的影响。为验证数值模型的合理性，Gilbert等[6]对2根两跨非预应力连续组合梁进行了为期340 d的长期性能试验。Dezi等[7]采用逐步分析法和积分中值定理，对采用柔性剪力连接件的预应力钢−混凝土组合梁进行了简化时随分析。王军文等[8]编制了预应力组合梁时效行为分析的计算程序，程序中考虑了单元的分层建造，张拉预应力筋、结构体系转换、施工外荷载的影响以及各节段混凝土龄期的不同所导致的收缩、徐变差异等。樊健生等[9]考虑混凝土收缩徐变和负弯矩区混凝土开裂对组合梁长期性能的影响，采用逐步计算法对其计算模型进行了求解。王文炜等[10]采用换算弹性模量法建立了考虑混凝土收缩徐变的增量微分模型，根据边界条件求出了各项力学性能指标的闭合解。聂建国[11]从组合梁的截面自内力平衡和变形协调出发，建立了考虑混凝土收缩、徐变影响的组合梁长期刚度计算公式。《钢结构设计规范》(GB 50017—2003)和《铁路结合梁设计规定》(TBJ 24—89)仅规定了对非预应力钢−混凝土组合梁长期变形的计算方法。综上所述，迄今国内外对钢−混凝土组合梁的长期性能已进行了一定的研究，但仍存在以下问题：未开展城市轻轨钢−混凝土组合梁长期性能(包括正常运营阶段和施工阶段)的研究；针对非预应力组合梁的长期性能试验研究较为深入，而预应力组合梁的试验研究较少，等。鉴于此，本文作者对4根1:5(尺寸相似比)城市轻轨钢−混凝土组合梁模型进行堆载试验，对其在预应力筋张拉完成至施加二期荷载的90 d施工阶段的受力性能进行了研究，并提出了其在施工阶段跨中变形的简化设计建议。

1 试验设计

1.1 试件设计

以城市轻轨工程中实际采用的钢−混凝土组合梁为原型，按组合截面刚度和应力相似为原则，设计了4根尺寸相似比为1:5钢−混凝土组合梁模型，包括3根体外预应力钢−混凝土组合梁和1根非预应力钢−混凝土组合梁，编号分别为PCB−1，PCB−2，PCB−3和CB−1。预应力组合梁PCB−1中预应力筋配置原则是预应力抵消一期恒载＋二期恒载。试件的具体参数见表1。

4根试件的截面形状与尺寸均相同，梁长为5 m，计算跨度为4.8 m，混凝土板厚为100 mm，组合截面高为300 mm，混凝土板宽为600 mm。混凝土板和钢梁通过栓钉连接，栓钉沿梁全长间距为 100 mm，单排布置。试件施工图见图1。

试件中混凝土配合比见表2，自然养护，其材料特性见表3。钢梁采用I20b型钢，栓钉采用上海高强度螺栓厂生产的型号为GB10433 16 mm×80 mm(直径×长度)的圆柱头焊钉，预应力筋采用高强低松弛无黏结钢绞线。型钢、栓钉、预应力筋及普通钢筋材料特性如表4所示。

表1 试件参数Table 1 Parameters of test specimens

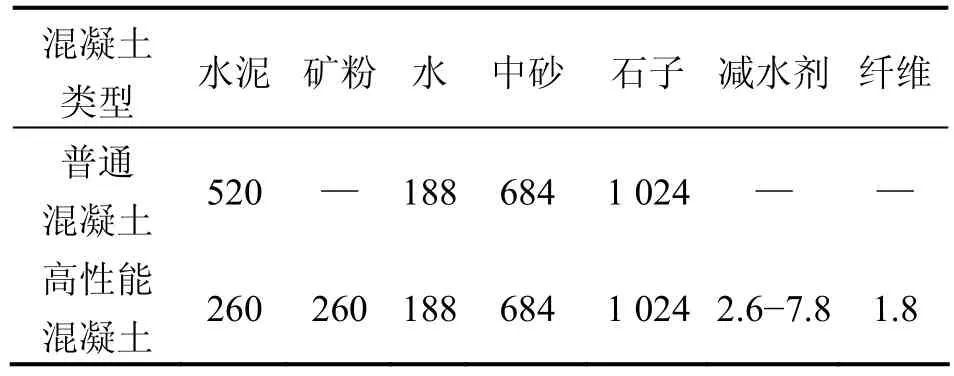
表2 混凝土配合比Table 2 Mix properties of bonding agents kg/m3

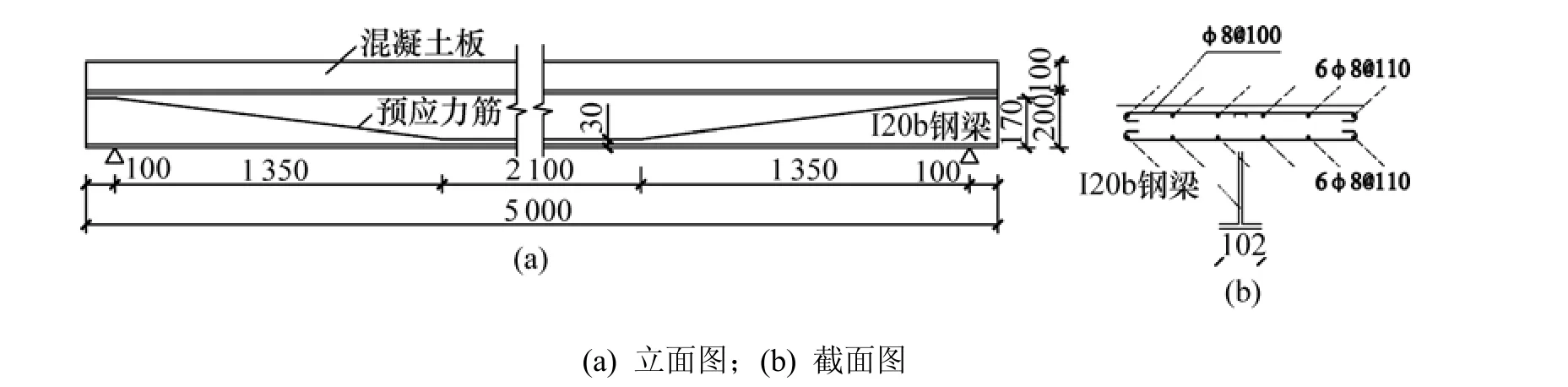
图1 试件施工图 (单位：mm)Fig.1 Details of specimens

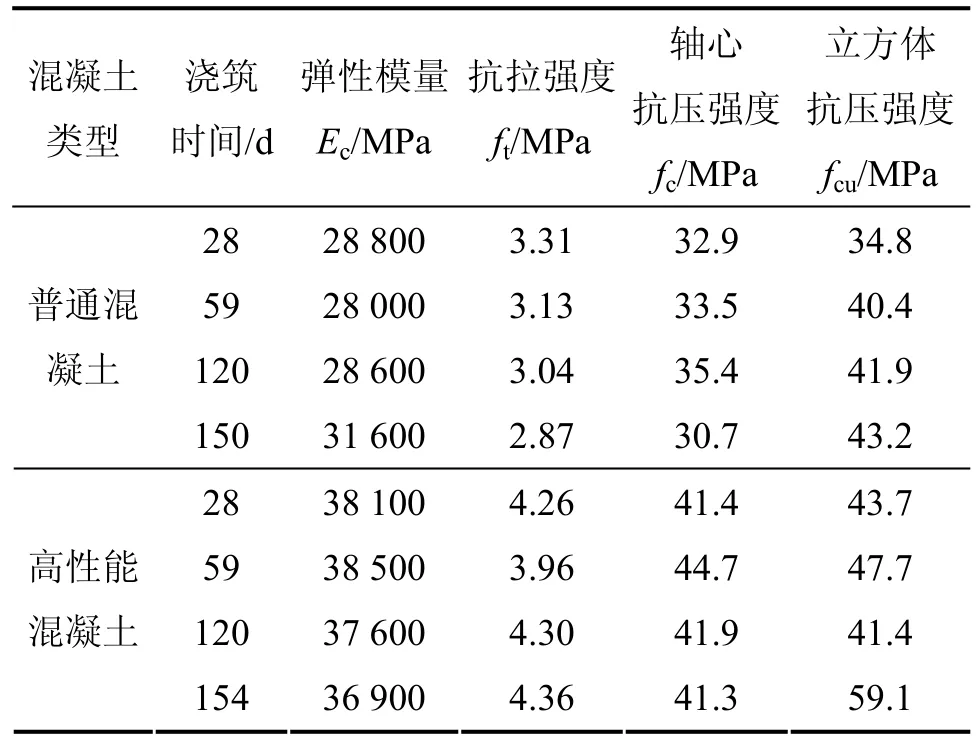
表3 混凝土材料特性Table 3 Mechanical properties of concrete

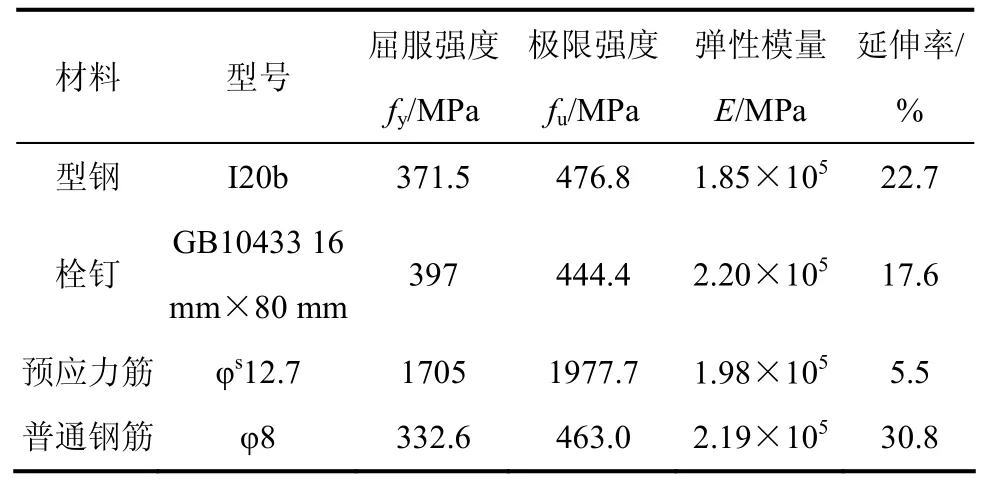
表4 型钢、栓钉、预应力筋及普通钢筋材料特性Table 4 Mechanical properties of materials

1.2 预应力筋张拉与量测方案

为保证混凝土强度得到充分发展，减小混凝土收缩、徐变对长期性能的影响，在试件浇筑养护62 d时张拉预应力筋。张拉过程为：0→A0.25σcon→B0.5σcon→A0.75σcon→B1.0σcon→持荷 1 min 后锚固→A1.0σcon→持荷1 min后锚固(注：A和B表示组合梁两侧的体外预应力筋，σcon为张拉控制应力)。张拉完成时预应力筋实测有效应力σpe如表5所示。

在预应力筋张拉过程中，试样 PCB−1，PCB−2和 PCB−3中混凝土板与钢梁之间均产生了一定的相对滑移，当张拉完成锚固时，PCB−1，PCB−2和PCB−3的梁板相对滑移实测值分别为0.143 3，0.18和0.043 3 mm。这表明：有效预应力越高，梁板相对滑移值越大；采用高性能混凝土可以减小梁板相对滑移。

表5 张拉完成时σpe实测值Table 5 Measured stress σpe after prestressing MPa

在张拉预应力筋的同时施加一期恒载以模拟梁自重。另外，为降低混凝土徐变对模型梁长期性能的影响，应尽量推迟二期恒载的施工时间，一般在张拉完成2～3月后施加二期恒载，故本试验在张拉完成90 d时施加二期恒载。一期恒载与二期恒载均采用 300 mm×250 mm×150 mm(长×宽×高)混凝土试块模拟，具体结果见表6。

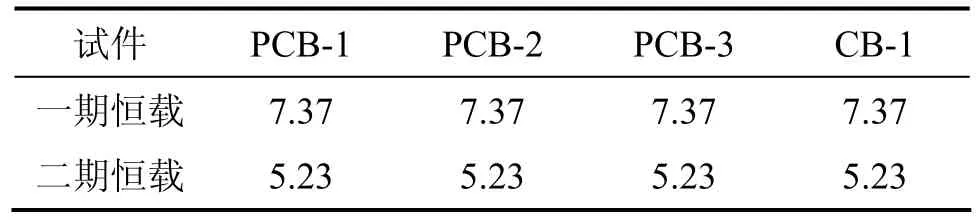
表6 试样恒载Table 6 Dead loading on samples kN/m

在长期试验过程中，主要量测内容包括：跨中变形、跨中截面曲率、预应力筋有效预应力、混凝土板应变、钢梁应变、混凝土板与钢梁之间的相对滑移和环境温度和相对湿度等。

2 主要试验结果与分析

2.1 环境温度和湿度的影响

以预应力筋张拉完成时为起点，在90 d施工阶段的持续时段内，环境温度和环境相对湿度的时随变化规律如图2和图3所示，均以张拉完成时的相应值为基准值。

2.2 跨中变形

在90 d施工阶段，4根组合梁试件跨中变形时程

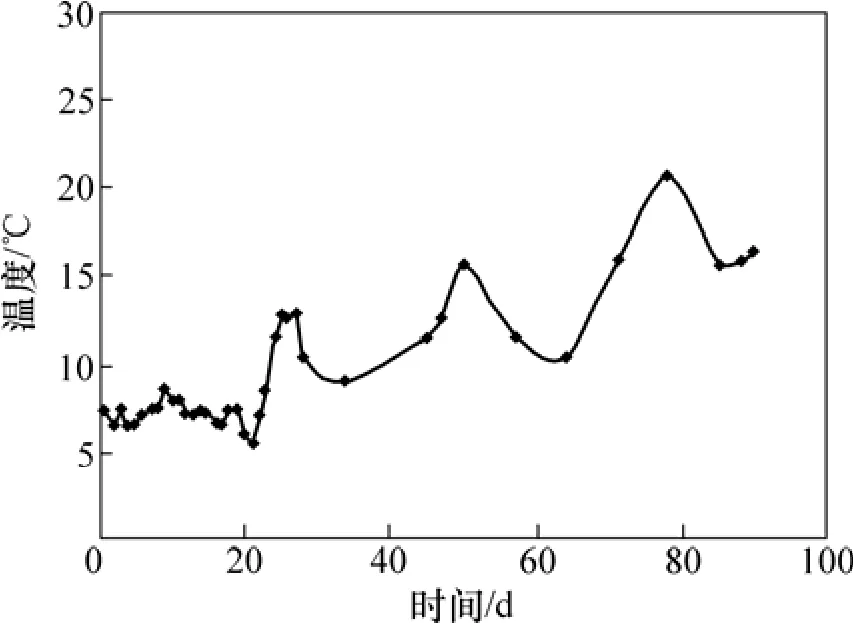
图2 环境温度时程曲线Fig.2 Environmental temperature-time curve

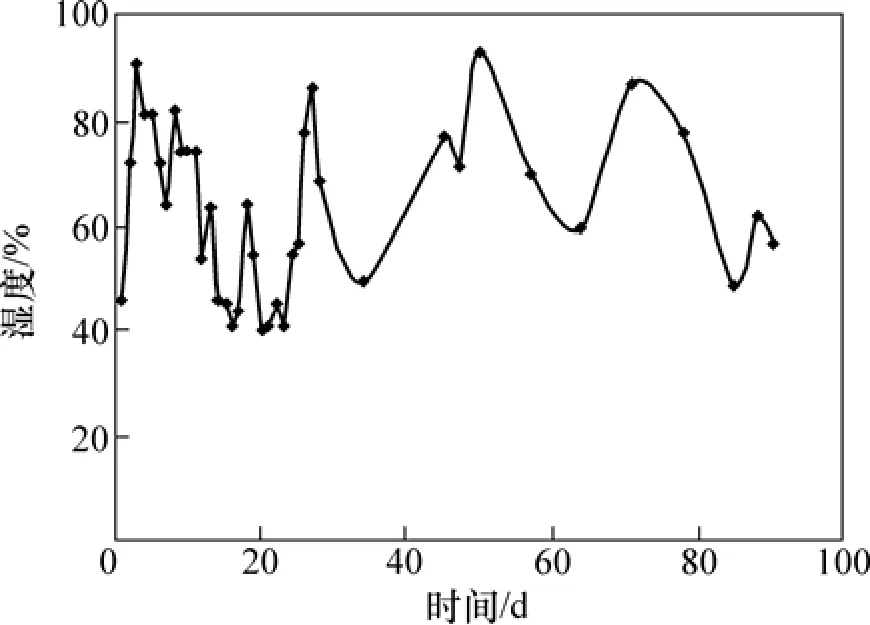
图3 环境相对湿度时程曲线Fig.3 Environmental relative humidity-time curve

曲线如图4所示。从图4可见：由于施工阶段混凝土收缩、徐变和预应力筋松弛三者的共同影响，试件PCB−1，PCB−2，PCB−3和 CB−1跨中变形分别增加了1.456，1.072，0.453和1.122 mm。其中，试样 PCB−2的附加变形比试样PCB−1的减小了26.4%，这表明有效预应力越高，组合梁跨中附加变形越小；试样PCB−3的附加变形比试样PCB−1的减小了68.9%，这证明了采用高性能混凝土可以减小组合梁的跨中附加变形；试样CB−1比试样PCB−1的附加变形小22.9%，但比试样PCB−2的附加变形大4.7%，说明预应力对组合梁变形的影响比较复杂，有待进一步研究。

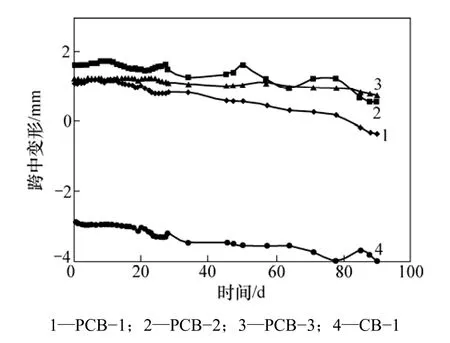
图4 组合梁跨中变形时程曲线Fig.4 Time-dependent deformation in mid-span of composite beams

2.3 跨中截面曲率

在90 d施工阶段内，组合梁跨中截面曲率时程曲线如图5所示。在施工阶段，试件PCB−1，PCB−2，PCB−3和 CB−1的跨中截面曲率变化量分别为0.300 8×10−6， 0.280 7×10−6， 0.205 2×10−6和0.222 9×10−6mm−1。可见，组合梁跨中截面曲率的变化规律与跨中变形基本相同，组合梁在施工阶段不断下挠。

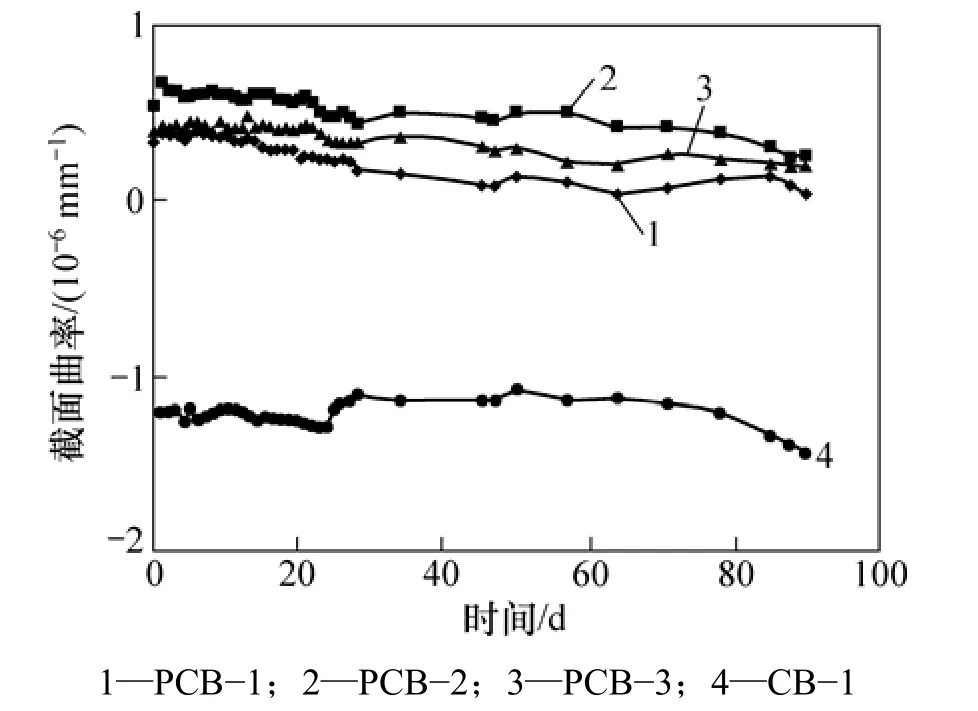
图5 组合梁跨中截面曲率时程曲线Fig.5 Time-dependent cross-section curvature in mid-span of composite beams

2.4 预应力筋有效应力

预应力筋有效应力在张拉完成后的90 d内的变化规律如图6所示。3根预应力组合梁试件中，有效预应力的变化规律基本相同。在整个90 d施工阶段内，试样PCB−1，PCB−2和PCB−3的有效预应力分别降低29.5，36.8和35.0 MPa，试样PCB−2的预应力损失比试样PCB−1和试样PCB−3分别大24.7%和5.1%。这表明初始有效预应力越高，施工阶段内的预应力损失越大，而且在张拉完成后的前20 d内，初始有效预应力越大，有效预应力的降低速率也越大。

2.5 混凝土板上缘应变

距跨中截面混凝土板上缘 15 mm处的混凝土应变在90 d施工阶段内的变化规律如图7所示。试样PCB−1，PCB−2，PCB−3和 CB−1的混凝土板上缘应变增量分别是 134με，101με，97με和 293με，显然非预应力组合梁CB−1的混凝土板上缘应变增加速率明显比预应力组合梁PCB−1，PCB−2和PCB−3的大；PCB−2和PCB−3比PCB−1的混凝土板上缘应变增加速率都要小，这表明有效预应力越高，混凝土板上缘应变增加速率都要小，采用高性能混凝土，可以降低混凝土板上缘应变增量。

2.6 钢梁下缘应变

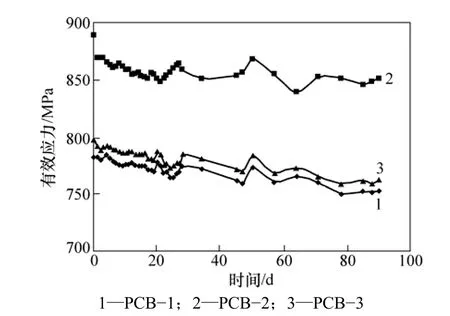
图6 预应力筋有效应力时程曲线Fig.6 Time-dependent effective pretension

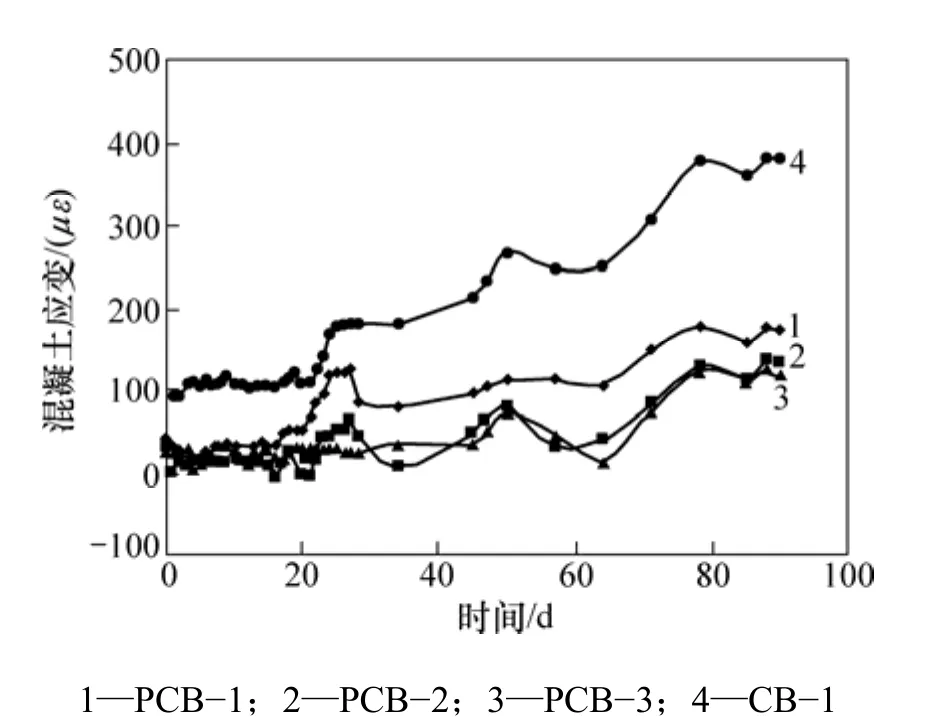
图7 混凝土板上缘应变时程曲线Fig.7 Time-dependent strain of extreme compression fiber in concrete slab

在90 d施工阶段内，跨中钢梁下缘应变的变化规律如图8所示。从图8可见：在张拉完成90 d内，组合梁试件跨中截面钢梁下缘应变的变化规律基本相同，变化幅度不大，但总体呈上升趋势。这是由于混凝的土收缩、徐变受到钢梁的约束，组合梁截面发生应力重分布。PCB−1，PCB−2，PCB−3和 CB−1的混凝土板上缘应变增量分别是 77με，50με，65με和 40με，可见，CB−1的钢梁下缘应变增加速率比 PCB−1，PCB−2和PCB−3的小，这表明非预应力组合梁比预应力组合梁的钢梁下缘应变增加速率小；PCB−2比PCB−1的钢梁下缘应变增加速率都要小，说明有效预应力越高，钢梁下缘应变增加速率越小；PCB−3比PCB−1的钢梁下应变增加速率也要小，表明采用高性能混凝土，可以减小钢梁下应变增加速率。

2.7 梁板相对滑移

在90 d施工阶段中，梁板相对滑移的变化规律如图9所示。试件PCB−1，PCB−2，PCB−3和CB−1的梁板相对滑移的变化量分别为 0.042 4，0.001 4，0.048 4和 0.024 8 mm。相比之下，试件 PCB−1和PCB−3的相对滑移值的变化速率比试件 PCB−2和CB−1的大。有效预应力及混凝土的种类对梁板相对滑移的影响规律不太明显。

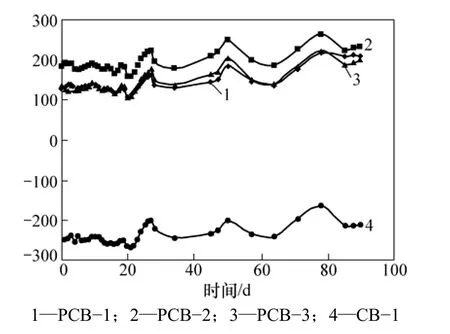
图8 钢梁下缘应变时程曲线Fig.8 Time-dependent strain of extreme tension fiber in steel beam

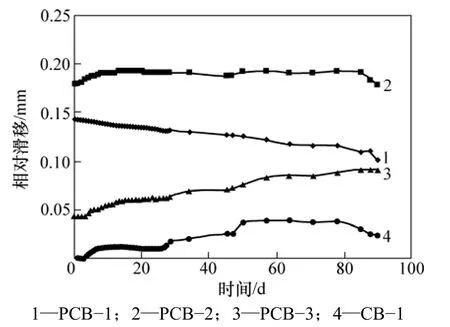
图9 梁板相对滑移时程曲线Fig.9 Time-dependent slip at steel-concrete slab interface of composite beam

3 施工阶段变形设计建议

在我国现行规范中，还未有针对预应力钢−混凝土组合梁长期变形的计算规定。对于非预应力钢−混凝土组合梁长期变形，《钢结构设计规范》(GB 50017—2003)规定，在计算组合梁长期挠度时，钢梁与混凝土板的弹性模量之比取2αE(αE为钢梁与混凝土板的初始弹性模量之比)；而《铁路结合梁设计规定》(TBJ 24−89)则建议取2.5αE。按这2种规范方法计算试件在施工阶段的附加变形值与试验实测值对比如表 7所示。可见：按规范计算的组合梁试件附加变形值误差较大，对试样PCB−1，PCB−2和CB−1来说偏小，而对试样PCB−3来说则偏大。

根据 PCB−1，PCB−2，PCB−3 和 CB−1 在 90 d施工阶段中的附加变形实测值，参照规范方法，可得到钢梁与混凝土板的弹性模量之比分别为 3.60αE，2.76αE，1.73αE，2.86αE。故建议：(1) 计算城市轻轨非预应力组合梁在90 d施工阶段中的跨中变形时，钢梁与混凝土板弹性模量比取 2.86αE。(2) 计算城市轻轨预应力组合梁在90天施工阶段中的跨中变形时，钢梁与普通混凝土板弹性模量比取3.18αE，钢梁与高性能混凝土板弹性模量比取1.73αE。

4 结论

(1) 在混凝土收缩、徐变和预应力筋松弛的共同影响下，组合梁不断下挠，其中试样PCB−1，PCB−2，PCB−3和CB−1跨中变形分别增加了1.456，1.072，0.453和1.122 mm。

(2) 在90 d施工阶段中，有效预应力较高的试样PCB−2的附加变形与试样 PCB−1的相比减小了26.4%，表明有效预应力越高，附加变形越小。

(3) 采用高性能混凝土可以明显减小组合梁跨中附加变形，试验中达到了68.9%。

(4) 张拉预应力筋时，钢梁与混凝土板之间产生相对滑移；而在90 d施工阶段中，梁板之间基本无相对滑移。

(5) 建议计算90 d施工阶段中城市轻轨非预应力钢−混凝土组合梁的跨中变形时，钢梁与混凝土板弹性模量比取2.86αE；计算城市轻轨预应力钢−混凝土组合梁的跨中变形时，钢梁与普通混凝土板弹性模量比取 3.18αE，钢梁与高性能混凝土板弹性模量比取1.73αE。

[1] 薛伟辰, 王巍. 轨道交通预应力混凝土梁施工阶段徐变性能研究[J]. 铁道学报, 2008, 30(1): 53−59.XUE Wei-chen, WANG Wei. Study on creep behavior of prestressed concrete beams for rail transportation during construction stage[J]. Journal of the China Railway Society,2008, 30(1): 53−59.

[2] 薛伟辰, 王巍. 城市轻轨预应力混凝土轨道梁徐变性能试验研究[J]. 铁道学报, 2006, 28(6): 93−98.XUE Wei-chen, WANG Wei. Experimental study on creep behavior of urban light rail prestressed concrete track girder[J].Journal of the China Railway Society, 2006, 28(6): 93−98.

[3] XUE Wei-chen, DING Min, HE Chi, et al. Long term behavior of prestressed composite beams at service loads for one year[J].ASCE, Structural Engineering, 2008, 134(6): 930−937.

[4] 樊健生, 聂建国, 王浩. 考虑收缩、徐变及开裂影响的组合梁长期受力性能研究(Ⅰ): 试验及计算[J]. 土木工程学报, 2009,42(3): 8−15.FAN Jian-sheng, NIE Jian-guo, WANG Hao. Long-term behavior of composite beams with shrinkage, creep and cracking(I): Experiment and calculation[J]. China Civil Engineering Journal, 2009, 42(3): 8−15.

[5] Bradford M A, Gilbert R I. Experiments on composite beams at service loads[J]. Trans Inst Eng Austr Civil Eng, 1991, 33(4):285−291.

[6] Gilbert R I, Bradford M A. Time-dependent behavior of continuous composite beams at service loads[J]. Journal of Structural Engineering, 1995, 121(2): 319−327.

[7] Dezi L, Leoni G, Tarantino A M. Time-dependent analysis of prestressed composite beams[J]. Journal of Structural Engineering, 1995, 121(4): 621−633.

[8] 王军文, 李建中, 梁志广. 预应力组合梁桥的时效分析[J]. 工程力学, 1998(增刊): 550−555.WANG Jun-wen, LI Jian-zhong, LIANG Zhi-guang.Time-dependent analysis of prestressed composite beams[J].Engineering Mechanics, 1998(Suppl): 550−555.

[9] 樊健生, 聂鑫, 李全旺. 考虑收缩、徐变及开裂影响的组合梁长期受力性能研究(Ⅱ): 理论分析[J]. 土木工程学报, 2009,42(3): 16−22.FAN Jian-sheng, NIE Xin, LI Quan-wang. Long-term behavior of composite beams with shrinkage, creep and cracking (Ⅱ):Theoretical analysis[J]. China Civil Engineering Journal, 2009,42(3): 16−22.

[10] 王文炜, 何初生, 冯竹林, 等. 钢—混凝土组合梁混凝土收缩徐变的增量微分方法[J]. 东南大学学报, 2010, 40(6):1252−1256.WANG Wen-wei, HE Chu-sheng, FENG Zhu-lin, et al.Incremental differential modeling of creep and shrinkage of steel-concrete composite beams[J]. Journal of Southeast University, 2010, 40(6): 1252−1256.

[11] 聂建国. 钢−混凝土组合梁长期变形的计算与分析[J]. 建筑结构, 1997(1): 42−45.NIE Jian-guo. Prediction and analysis for long-term deformation of composite beams of steel and concrete[J]. Building Structure,1997(1): 42−45.