基于马尔可夫链的自然风风向建模

季亮，谭洪卫，王亮

(同济大学 机械工程学院，上海，200092)

自然风是大气运动的结果，其风向、风速时刻都在发生变化。对于和自然风相关的科研领域，自然风风速、风向变化的基础数据和变化特征是至关重要的，例如：风能发电[1]，自然通风工程[2]，城市大气环境评价[3]，污染物排放扩散预测[4]等研究领域。然而，相关研究常常将自然风风速和风向视作一个稳态参数并选取某个时间段内平均风速和主导风向，以此作为边界条件进行研究。这种恒定风的假设，可能会导致研究结果偏离客观事实。因此，必须充分考虑风向和风速的动态变化。自然风动态变化的数据尽管可以通过气象台站的实测获得，但该方法存在诸多限制：获取实测数据耗费人力物力，也难免会存在数据缺失；实测的数据是历史数据，对于预测评估而言存在不足；尽管气象台站的实测全年的动态变化数据，但时间尺度不完全符合要求，一般气象台站可以向社会公开公布的月平均数据，另外通过购买气象产品可获得逐时变化的数据，但对于更小时间尺度的数据如逐分变化的动态数据则难以获得。对风向变化进行分析、基于数学方法对自然风进行数学建模，从而可以人工推演自然风变化尤为必要。国内外对自然风建模方法的基础理论及其应用已进行许多研究。例如，芮晓明等[5-7]在风电领域对自然风风速变化模型展开研究，为风力发电能力预测提供指导；Sahin等[8]以一阶马尔可夫链为基础，用土耳其实测的逐时风速序列，反演自然风风速的人工时间序列，证明尽管一阶马尔可夫链仅具有一阶的相关性，但90%符合客观风速分布，证实马尔可夫链在风速建模过程中的有效性；Kantz等[9-11]基于马尔可夫链的基本原理，以风速为研究对象，将自然风看作是随机变量的时间序列，基于逐时测试数据，对自然风进行建模；Dobigeon等[12-13]考虑风向和风速的联合相关性，然后进行自回归建模，但其采用的样本之间的时间跨度较大，而风向在这样的时间跨度内是相对稳定的，因而，其得到的风向模型仍是一个准静态模型。总体上，国内外基于马尔可夫链的基本原理，对自然风风向进行建模的研究较少，且在这些有限的研究中，没有关注到更小时间尺度(如逐分)的风向变化，未能充分反映自然风风向的动态变化特征。本研究以小时间尺度的风向变化为研究对象，基于马尔可夫过程的原理，求取一个36状态的转移矩阵，完整提出对风向进行建模并反向推演自然风风向变化时间序列的方法。同时，辅以上海中心城区的逐分实测得到自然风数据，获得当地的转移概率矩阵模型。

1 马尔可夫链模型

对于马尔可夫链，在随机过程等相关文献中有详细的阐述[14]。这里仅对本文用到的马尔可夫链基本原理进行基本简述。

马尔可夫链的基本特征为：在给定当前信息的情况下，当前的状态可以用来预测将来，过去的状态对于预测将来状态是无关的。

马尔可夫链是随机变量X1，X2，X3…的一个序列。这些变量的取值范围，即所有可能的取值的集合，被称为“状态空间”。根据马尔可夫链原理，Xn+1取得某状态的概率仅和Xn相关，即：

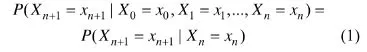
其中：P(·)表示概率函数；Xi为时间序列的第i个随机变量；xi为第i个随机变量的状态值。

该等式的含义是：当Xn的状态值是xn时，第Xn+1的状态值为xn+1的概率是一定的，且仅和Xn相关。

2 基于马尔可夫链的自然风风向的建模方法

马尔可夫链是常用的随机过程之一，但针对风向建模较为少见，且对本文所关注的小时间尺度风向建模而言，有2个新特点：首先是风向的状态空间和风速不同，风向状态空间是一个360°圆周角中的值，将某一个风向角设定为固定的状态是不合理的；其次对小时间尺度而言，自然风风向的波动特性明显，而不像较大时间跨度情况下风向较为稳定。因此，小时间尺度的状态变化程度会显著高于大时间尺度。

自然风风向建模包含2个方面 (如图1所示)：首先应当根据当地历史数据和马尔可夫链提出的风向建模方法，构建当地风向变化的转移概率模型；其次，根据获取的概率转移模型，反向推演，以预测当地的风向变化。

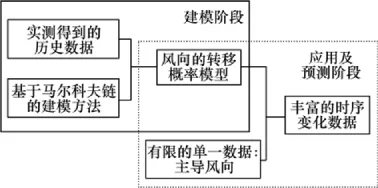
图1 风向建模的流程Fig.1 Flow chart of wind direction modeling

2.1 以马尔可夫链对自然风风向建模的步骤

2.1.1 确定状态空间

自然风风向具有的最主要特点是：在一定的时间跨度内具有一个主导风向，即该风向出现的频率最高，总持续时间最长。因此，将主导风向定义为状态值0。并以此为基础，每顺时针增加10°就将状态值取值加1，每逆时针增加10°就将状态值取值减1，这样，在360°的圆周角范围内共有36个状态值。表1所示为风向的状态空间。

2.1.2 风向的转移概率模型

对某个时刻而言，该时刻有可能取得其状态空间中的任何状态，只是取得各不同状态的概率不同，根据前述内容，后一个时刻达到某状态的概率与前一个时刻的状态有关，该特性可以表示为式(2)。其取得所有状态值的概率的和为1，可以表示为式(3)。

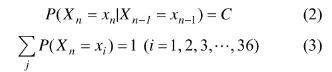
其中：C为一个常数；Xn和Xn-1分别为第n个和第n-1个时刻的状态；xi为第i个状态。在本文中，共定义36个状态，因此，xi有36个取值。

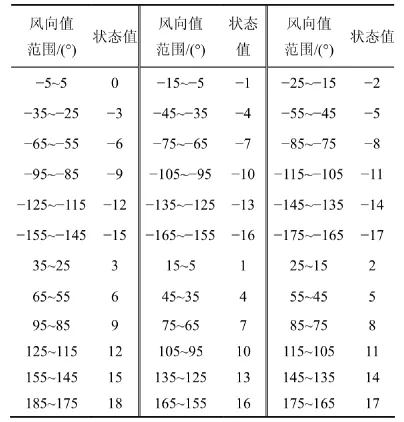
表1 各风向角度状态值Table1 Status value of wind direction

基于马尔可夫链的这种性质，可以定义一个“转移概率矩阵”。该矩阵表示当前一个时刻取值xi时，后一个时刻取值xj的概率。矩阵中的每一个元素均表示一个转移概率。用Pij来表示转移矩阵中的1个元素，则Pij可表示为式(4)，转移矩阵可以表示为P(式(5))。

其中：Pij从当前的状态i到下一个状态j的概率；P转移概率矩阵。

对于P，可通过分析历史的实测样本数据求得。到此，已经完成对自然风风向变化的建模。转移概率矩阵P中的任意1个元素，表示当前时刻的风向值与下一个时刻的风向值的条件概率关系。因此，P以转移概率的方式，建模并表达自然风风向变化。

2.2 基于转移概率模型对风向进行反演和预测

2.2.1 基于转移矩阵求取叠加转移矩阵

根据式(3)，对P中的任何一行均有下式成立：

据此，对P按照式(7)进行转化，使之成为P′(为便于区分，用k和l分别表示新矩阵P′的行和列的编号)。将P′称为P的“叠加转移矩阵”。

矩阵P′的物理意义是：P′中任意一行第N个元素的值是P中该行的第1列元素到第N个元素的和。易知P′的最后一列均是1。

2.2.2 耦合叠加转移矩阵和随机数，以主导风向反演风向动态变化时序列

根据叠加转移矩阵本身的特点，即可通过计算机随机数来反向推演风向时间序列。

为便于分析，假定风向只有4个状态，其状态值分别为1，2，3和4(分别代表东、南、西、北4个风向)。

首先通过当地已有的历史数据得到转移矩阵P。假设P为：

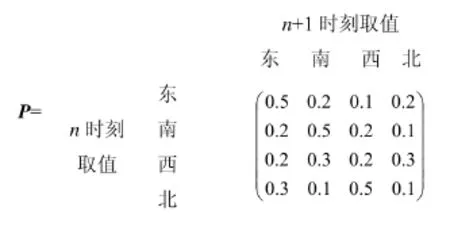
矩阵P更加直观地说明转移矩阵的意义。如，当Xn时刻出现了东风时，那么，Xn+1时刻出现东风的概率为0.5，出现南风和北风的概率为0.2，出现其完全反方向的风(西风)的概率为0.1。矩阵P的叠加转移矩阵则为：

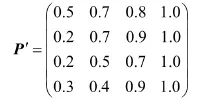
假定当日的主导风向为南风，则令初值X1=2(南风)，通过计算机随机生成1个介于0到1之间的随机小数，假定此值为0.392。那么，对第2行而言，该值落在第1个元素和第2个元素之间。因此，可以认为下一个时刻(X2)的状态值转移为第2列所表达的状态(仍然是南风)。然后，将X2=2(南风)作为初始值，以相同方法求取X3。依此类推，直到求取到指定的时间长度Xn。

2.3 马尔可夫过程对自然风进行建模与反演的合理性分析

耦合随机数和基于马尔可夫链原理的转移矩阵的合理性在于：一方面，计算机随机数本身是0到1之间一个平均分布；另一方面，转移矩阵则体现当前状态对下一状态的影响程度，转移矩阵中的任何1个元素Pij代表从状态xi到状态xj可能性，因此，转移矩阵体现状态之间相互转移的概率，体现变化的权重程度。随机值的平均分布体现所有可能的状态空间，而转移矩阵则反映状态值转移的不同可能性。这2个不同的分布函数的结合使用，完整地重现自然风时序列的物理意义，因此，该方法是合理、有效的。

3 实例应用：上海中心城区风向建模

以下基于上海地区小尺度连续采样的实测数据，为上海城区的风向变化进行建模。建立测点对上海中心城区风向进行长期高频采集。以1 min为样本取样间隔，在上海中心城区某高楼的顶部设立小型气象站(超声波流量计)连续计测自然风数据。方圆350 m内，均无高于该楼的建筑，可认为无论风向从何而来，测点均不处于其他建筑的绕流区内。

3.1 用于求取马尔可夫链的时序列样本简介及处理

在进行建模之前，首先必须对风向本身的变化特征进行系统分析，从而能对样本进行优化。为便于展示，下面选取大量测试数据中具有代表性的一段，对自然分风向变化特征进行说明(见图2和图3)。

从图2和图3可见自然风风向的基本变化特征如下：(1)逐时主导风向在一段时间内较稳定；(2)逐分的风向则时刻都在随机变化；(3)风向主要在当日主导风向两侧较小的范围内小幅度变化。需要说明的是：在图2中第840 min至第1 080 min的时间段内的变化，容易产生风向变化幅度增大的误解，但因为Y轴的物理量是圆周角，图2中的-180°和+180°之间的风向差值并非360°，而是0°，因此，风向变化幅度仍然是小幅度的。

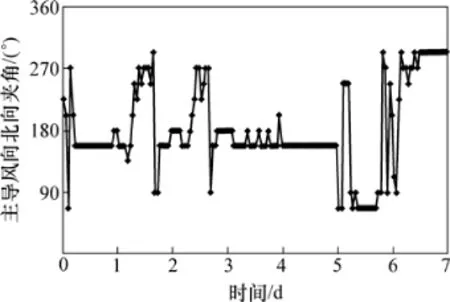
图2 1周内的逐时风向变化图Fig.2 Hourly variation of wind direction for a week

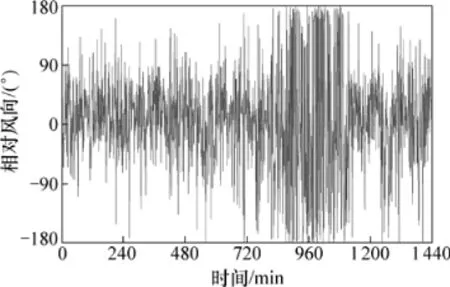
图3 1日内逐分风向变化图Fig.3 Minutely variation of wind direction with day

由于存在上述特征，在进行风向建模前，首先对自然风风向进行“分段中心化处理”，即将所有的的测试样本按照主导风向不同分为不同的时间段；其次，将所有的时间段以当段内的主导风向为中心，求取其“相对”夹角，而非测试仪器测量得到的“北向夹角”，并将“相对夹角”的数据全部重新连接成随机序列。

这样处理后的样本，可消除大气环流导致的风向变化(这种风向变化是和地球公转、自转运动的结果)带来的影响，而关注本文所研究的焦点是小时间尺度的随机变化。根据上述分析和“中心化”后，本文共在6个月的测试数据内获得大约900 000个逐分的时序列样本，测试时间跨度是上海地区的2009年10月20日至2010年4月10日。

3.2 自然风风向建模及反演风向时序列

采用前面所述的方法，基于处理后的时序列样本，构建上海地区的风向变动转移概率矩阵模型(如图4所示)。由于页面尺寸限制，图4中的转移概率矩阵仅表示2位有效数字。然后，以该转移概率矩阵为基础，进行反向推演分析，推演结果如图5所示。

从图5可见：人工反演的自然风风向，其振幅和变化范围均与实测值接近。经过统计计算，反演的时间序列样本和实测时序列样本的均值、方差、频率分布(见图6)非常接近，其中：实测样本的均值为285.7°，标准差为24.5°；反演样本的均值为285.8°，标准差为23.5°；各风向分布直方图如图6所示。

由图6可见：该方法得到的风向变化时序列的统计特性和历史数据具有良好相似性，且充分反映动态变化，对预测未来风向变化，从而将其应用于其他学科作为基础数据而言有重要的意义。

图4 上海中心城区的风向变化转移概率矩阵Fig.4 Transition matrix of wind direction variation in urban area of shanghai

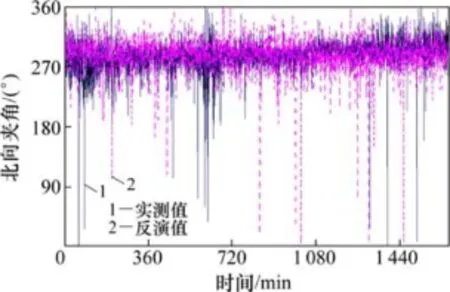
图5 人工反演的风向变化时间序列Fig.5 Artificially generated minutely time series for wind direction variation

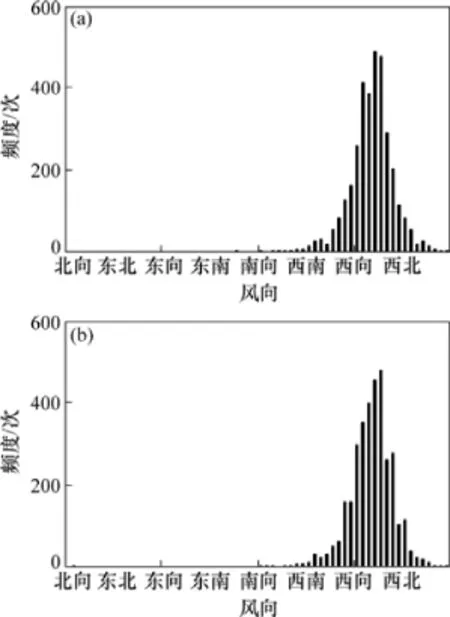
图6 实测样本和反演样本的风向频度分布直方图Fig.6 Frequency distribution of measured data and generated data

4 结论

(1)提出基于马尔可夫过程的基本原理的自然风风向的计算机建模方法，阐释该方法的有效性和合理性。

(2)基于上述方法和实测数据，构建上海地区的概率转移矩阵，可为相关研究提供参考。

[1]LI Gong, SHI Jing.Application of Bayesian model averaging in modeling long-term wind speed distributions[J].Renewable Energy, 2010, 35(1): 1192-1202.

[2]张国强, 阳丽娜, 周军莉, 等.自然通风潜力评估体系的建立与应用[J].湖南大学学报: 自然科学版, 2006, 33(1): 25-28.ZHANG Guo-qiang, YANG Li-na, ZHOU Jun-li, et al.Development and application of natural ventilation potential evaluation system[J].Journal of Hunan University: Natural Science, 2006, 33(1): 25-28.

[3]黄小培, 覃峥嵘, 韦革宁.桂西酸雨的季节分布及风向频率统计特征分析[J].气象研究与应用, 2008, 29(4): 10-13.HUANG Xiao-pei, QIN Zheng-rong, WEI Ge-ning.Seasonal distribution characteristics of acide rain in the west of Guangxi and statistic characteristics of wind direct[J].Journal of Meteorological Research and Application.2008, 29(4): 10-13.

[4]王嘉松, 陈达良, 黄震, 等.实际大气条件下汽车尾气扩散的模拟与观测[J].上海交通大学学报, 2005, 39(11): 1891-1894.WANG Jia-song, CHENG Da-liang, HUANG Zhen, et al.The prediction and field observation for pollutant dispersion fromvehicular exhaust plume in real atmospheric environment[J].Journal of Shanghai Jiaotong University, 2007, 28(12):1335-1338.

[5]芮晓明, 马志勇, 康传明.小尺度风特性建模与分析[J].太阳能学报, 2007, 28(12): 1335-1338.RUI Xiao-ming, MA Zhi-yong, KANG Chuan-ming.Modeling and analysis of wind characteristics with little periods[J].Acta Energiae Solaris Sinica, 2007, 28(12): 1335-1338.

[6]曹娜, 赵海翔, 任普春.风电场动态分析中风速模型的建立及应用[J].中国电机工程学报, 2007, 27(36): 68-71.CAO Na, ZHAO Hai-xiang, REN Pu-chun, et al.Establish and application of wind speed model in wind farm dynamics analysis[J].Proceedings of CSEE, 2007, 27(36): 68-71.

[7]Dunn R W, Li F, Miranda M S.Generation adequacy studies using new spatially correlated wind speed modeling[J].Advances of Power System & Hydroelectric Engineering, 2007,23(11): 45-52.

[8]Sahin A D, Sen Z.First-order Markov chain approach to wind speed modeling[J].Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(3/4): 263-269.

[9]Kantz H, Holstein D, Ragwitz M, et al.Markov chain model for turbulent wind speed data[J].Physica A: Statistical Mechanics and its Applications, 2004, 342(1/2): 315-321.

[10]Shamshad A, Bawadi M A, Hussin W, et al.First and second order Markov chain models for synthetic generation of wind speed time series[J].Energy, 2005, 30(5): 693-708.

[11]Pourmousavi K S A, Ardehali M M.Very short-term wind speed prediction: A new artificial neural network–Markov chain model[J].Energy Conversion and Management, 2011, 52(1):738-745.

[12]Dobigeon N, Tourneret J.Joint segmentation of wind speed and direction using a hierarchical model[J].Computational Statistics& Data Analysis, 2007, 51(12): 5603-5621.

[13]Carta J A, Ramírez P, Bueno C.A joint probability density function of wind speed and direction for wind energy analysis[J].Energy Conversion and Management, 2008, 49(6): 1309-1320.

[14]刘次华.随机过程[M].第四版.武汉: 华中科技大学出版社,2008: 26-30.LIU Ci-hua.Stochastic process[M].4th Ed.Wuhan: Huazhong University of Science and Technology Press, 2008: 26-30.