横风作用下货车篷布结构强度计算

熊小慧，梁习锋

(1. 中南大学 轨道交通安全教育部重点实验室，湖南 长沙，410075；2. 中南大学 交通运输工程学院，湖南 长沙，410075)

货车篷布是铁路货车辅助用具，用于苫盖敞车装运的怕湿、易燃货物和其他需要苫盖的货物，在铁路货运中占有重要的地位。长期以来，由于我国铁路货运集装化程度不高，棚车数量相对有限，大部分货物(如粮食、化肥等)运输都是采用敞车苫盖篷布的运输方式。当苫盖篷布货车在大风地区运行时，篷布、篷布绳索、篷布绳网受到的气动力增大，经常出现篷布和篷布绳索脱落的现象，造成信号设施损坏及人身伤亡，在我国曾多次出现因篷布绳索脱落打伤、打死正在瞭望的机车乘务员和接车的车站助理值班员的重大安全事故[1−4]；同时篷布、篷布绳索和篷布绳网容易造成货物湿损和被盗，甚至引起火灾，严重影响货物安全及铁路运输形象；当货车在电气化铁路线上运行时，篷布、篷布绳网脱落还会造成接触网受损的重大行车事故。目前，我国铁路篷布、篷布绳索和篷布绳网标准和技术条件主要依据国外相关标准和现场经验制定，迄今为止，国内外相关学者对复杂工况下铁路货车篷布受力情况的研究和综合试验较少。面临我国铁路货运的快速发展，亟待对复杂工况下铁路货车篷布、篷布绳索和绳网的受力情况进行全面分析和评估，为制定符合我国铁路运输实际的篷布、篷布绳索和篷布绳网技术指标和安全运行条件提供依据。本文作者首先采用基于三维、不可压、非定常N-S方程和k−ε双方程湍流模型的数值求解方法对大风作用下的篷布内外空间复杂三维流场进行数值模拟计算[5−9]，得到篷布在各种复杂工况下所受气动载荷，为篷布强度计算提供加载数据；然后，采用索膜结构载荷分析理论，以篷布所受气动升力作为加载载荷，运用非线性有限元方法分析大风条件下的篷布强度。

1 大风作用下货车篷布空气动力学计算模型及假设

为了保证数值计算的准确性和计算机资源的有效利用，对敞车计算模型进行如下简化：省略车辆细微结构，如车钩等装置；采用四车联挂(机车和3节苫盖篷布敞车)。篷布采用 D 型铁路篷布(其长×宽为 15 m×5.3 m，面积为79.5m2)。同时，为模拟篷布内外表面空气的流动情况，采用零厚度壁面单元模拟篷布，忽略了篷布与空气之间的流固耦合效应。具体计算模型示意图见图1～2。

当模拟苫盖篷布货车在大风区域运行时，模型长度方向尺寸的选取则是使计算区域下游边界尽可能远离列车尾部，以避免出口截面受到列车尾流的影响，便于出口边界条件的给定；宽度需避免阻塞效应影响；计算区域的长度为400 m，宽度为300 m，高度为80 m，如图3所示。

图1 货车编组计算模型示意图Fig.1 Calculation model of train marshalling

图3 数值计算区域Fig.3 Calculation domain

采用合成风方法进行模拟计算，通过给定计算区域入口速度的方法综合考虑列车运行速度与风速的影响[10−11]。入口ABCD和ABFE为速度入口条件；出口EFGH和CDHG为压力出口，静压为0 MPa；地面(即ADHE面)给定滑移边界条件，方向与车速方向相反，大小相等，以体现与列车之间的相对运动。流域的顶面与两侧面以及车体表面给定光滑的无滑移壁面边界条件。采用非结构化网格对计算区域进行离散。计算模型总网格数为160万左右。具体篷布敞车网格如图4所示。

图4 篷布敞车网格图Fig.4 Mesh of freight vehicle and tarpaulin

2 横风作用下货车篷布强度计算模型及假设

由大风条件下货车篷布空气动力数值模拟计算分析可知：篷布在货车运行过程中主要承受向上的升力的作用，其在篷布绳索和篷布支架共同作用下的结构类似建筑结构里的索膜结构。这里利用ANSYS软件对篷布结构强度进行数值模拟计算。计算强度时，选取shell41单元作为篷布的单元类型，选取link10单元作为篷布绳索的单元类型[12−16]。

在计算篷布强度之前要进行以下假设：

(1) 索膜之间无相对滑动；索膜张拉变形为小应变；

(2) 膜材料为正交各向异性弹性材料，工作拉应力范围内为线性材料；

(3) 当篷布出现褶皱时，单元仍具有较小的刚度；

(4) 篷布与侧墙顶端接触处由于摩擦以及拉紧的作用，处于全约束状态；

(5) 由于摩擦的作用，在篷布结构上沿纵向的力对篷布的强度影响很小，可以略去。

根据以上有关数据信息以及假设，强度计算主要分为2个步骤：

(1) 利用 ANSYS建模，膜结构由于抗弯刚度很小，几何非线性较强，其变形主要是垂直膜面的位移，而膜结构本身的面内位移很小。因此，采用三角形等参元对其进行离散，加载面压力之后，对侧墙、端墙与篷布接触的地方进行全约束，通过几何非线性的计算，得到应力较大的区域，取出此区域和侧墙接触位置结点的约束反力。

(2) 建立与应力较大区域连接部分篷布模型，采用平面三角形单元离散，把所得的结点约束反力施加在模型中，对模型进行一定约束后，进行线性计算，即可得到最大应力点。

图5 篷布索膜结构计算模型图Fig.5 Calculation models of cable and membrane structure

图5所示为篷布索膜结构计算模型图和篷布顶部和侧面加载图，顶面加载数据来源于篷布空气动力学性能研究各个不同分区的所受气动力，具体加载数据见参考文献[10]，侧面加载数据则来源于篷布顶面计算之后的应力较大区域结点的约束反力。

3 大风条件下货车篷布强度结果分析

3.1 篷布强度影响因素分析

3.1.1 泊松比对篷布强度影响分析

由于篷布材料的固有特性，与弹性模量相比，其泊松比变化更大，为研究泊松比对篷布结构强度的影响，选取10种不同泊松比μ，分别为0，0.05，0.10，0.15，0.20，0.25，0.30，0.35，0.40 和 0.45。篷布厚度为0.5 mm，篷布弹性模量(包括经向和纬向)为1 100 MPa；篷布绳索的弹性模量为2 000 MPa，绳索直径为50 mm2，篷布绳索预应力取为100 N。图6所示为货车120 km/h通过大风地区，横风风速为20.7 m/s，篷布支架高为0.75 m时，不同泊松比下篷布顶面最大位移比和最大主应力比。最大位移比为不同泊松比的最大位移与泊松比为0时的最大位移之比；最大主应力比为不同泊松比的最大主应力与泊松比为0时的最大主应力之比。

由图6可以看出：

(1) 随着泊松比的增大，篷布顶面最大位移比和最大主应力比逐渐变小；

(2) 泊松比对最大位移的影响较大，当泊松比大于0.3之后，最大主应力比随泊松比的变化很小；

(3) 泊松比减小有利于增大最大主应力。由于考核篷布强度的需要，选取了最危险的工况进行计算，后面考核篷布强度时，选取篷布材料泊松比为0。

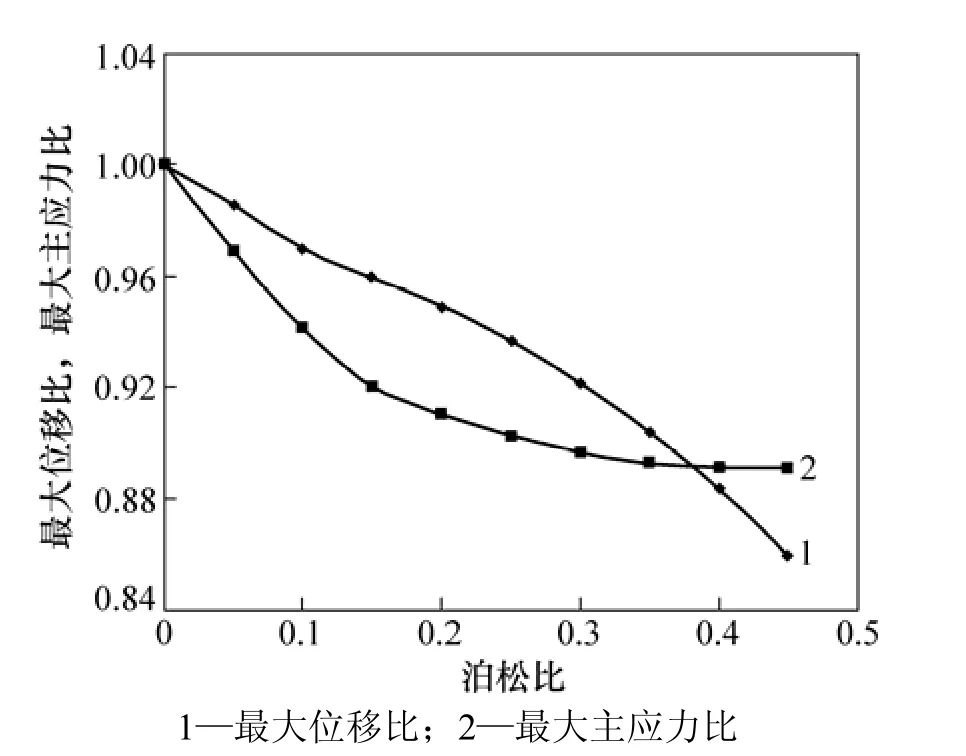
图6 篷布顶面最大位移比和最大主应力比随泊松比变化曲线Fig.6 Curve of maximum displacement ratio and principal stress ratio with Poisson's ratio

3.1.2 篷布绳索预张力对篷布强度影响分析

为研究篷布绳索张力对篷布强度的影响，选取 8种不同的绳索预张力来进行分析。选取的预张力为0，10，20，50，100，150，200 和 300 N。

选取篷布厚度为 0.5 mm，篷布弹性模量(包括经向和纬向)取为1 100 MPa，泊松比取为0；篷布绳索的弹性模量为2 000 MPa，泊松比取为0.3，绳索直径为50 mm。图7所示为货车120 km/h通过大风地区，横风风速为20.7 m/s，篷布支架高为0.75 m时，不同预张力下篷布顶面的最大位移比和最大主应力比。最大位移比为不同预张力的最大位移与预张力为0 N时的最大位移之比，最大主应力比为不同预张力下最大主应力与预张力为0时的最大主应力之比。

由图7可以看出：随着篷布绳索预张力的增大，篷布顶面最大位移比和最大主应力比逐渐变小；篷布绳索预张力的增大有利于减小篷布顶变形和最大主应力比；根据篷布实际运用需要，篷布强度校核时，选取篷布绳索预张力为100 N。

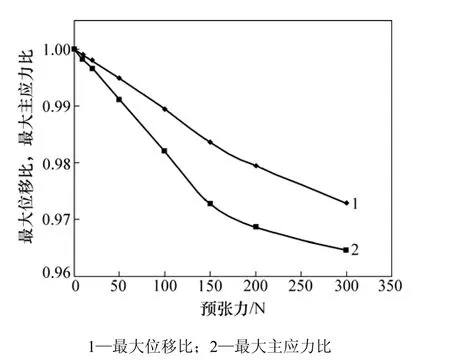
图7 篷布顶面最大位移比和最大主应力比随绳索预张力变化曲线Fig.7 Curve of maximum displacement ratio and principal stress ratio with tarpaulin rope pretension

3.2 不同工况下篷布强度计算

图8和图9所示分别为篷布顶面、篷布网眼的最大位移和最大主应力随车速和风速的变化曲线。图10所示为货车以120 km/h速度通过大风地区，横风风速为31.5 m/s时，篷布顶面、侧面的应力和变形。

由图8和图9可知：

(1) 篷布所受最大应力均发生在绳索与篷布连接的眼圈位置，篷布其他位置的应力均小于该位置应力；篷布网眼位置采用双层包边结构可以有效缓解该位置的最大主应力。

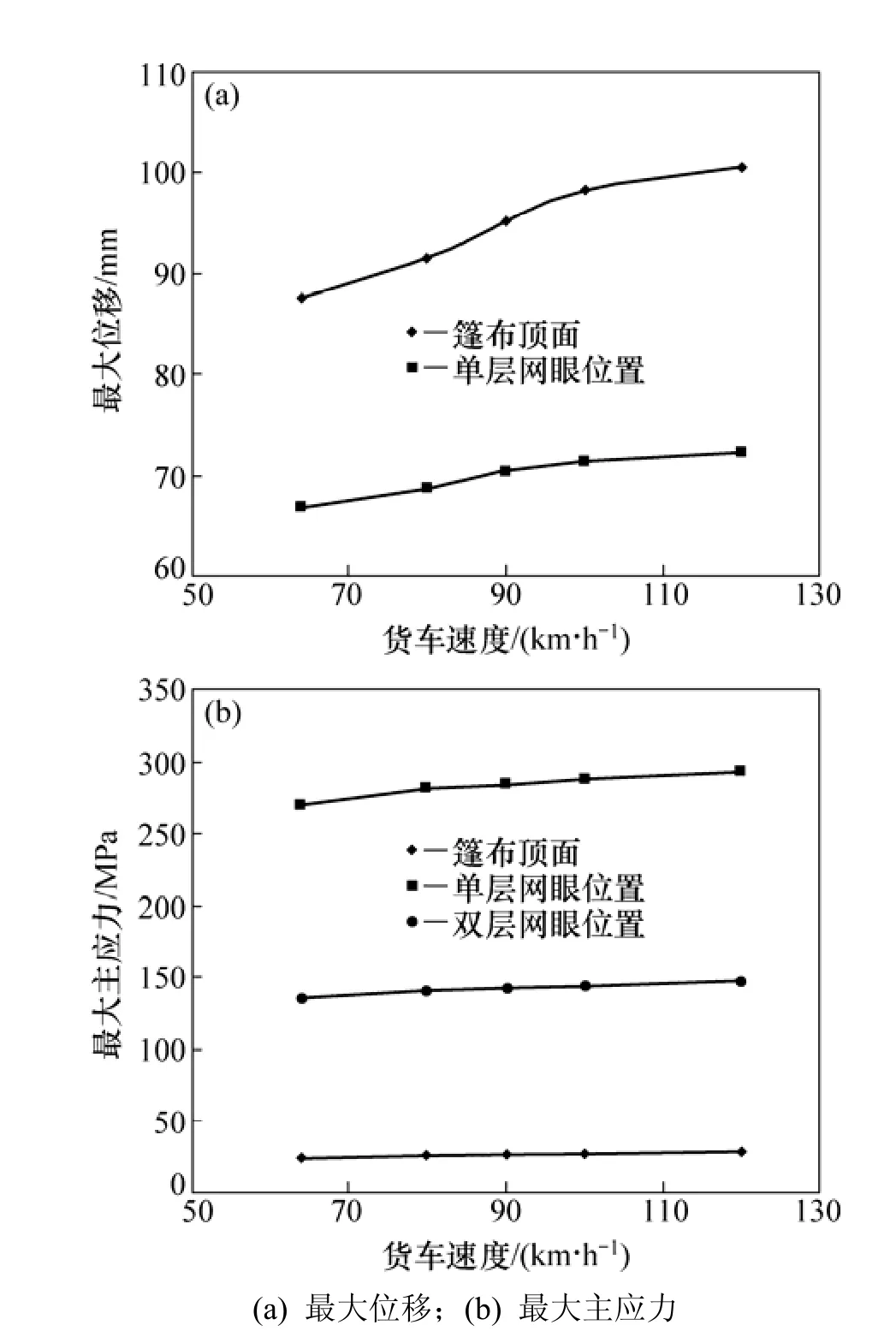
图8 最大位移和最大主应力随货车速度变化曲线Fig.8 Curve of maximum displacement and principal stress with freight train speed

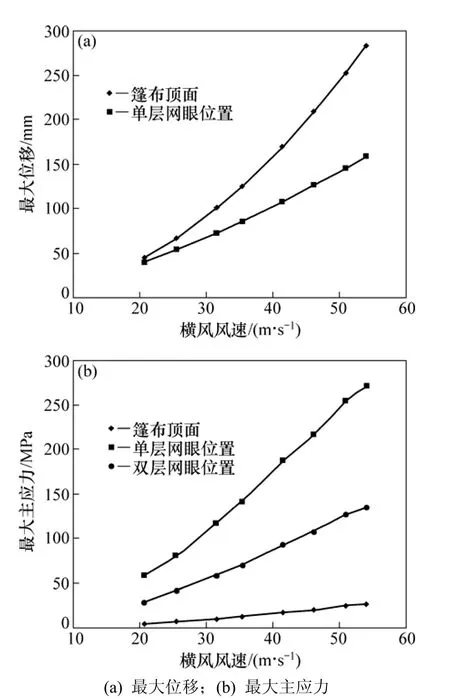
图9 最大位移和最大主应力随风速变化曲线Fig.9 Curve of maximum displacement and principal stress with side wind speed

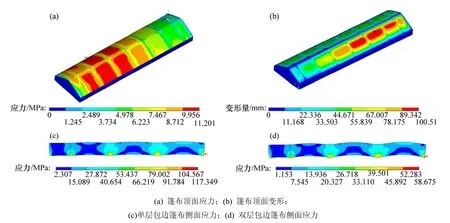
图10 货车速度120 km/h、风速31.5 m/s时，篷布强度计算应力图和变形图Fig.10 Stress and deformation of tarpaulin structure what train speed of 120km/h and wind speed of 31.5 m/s

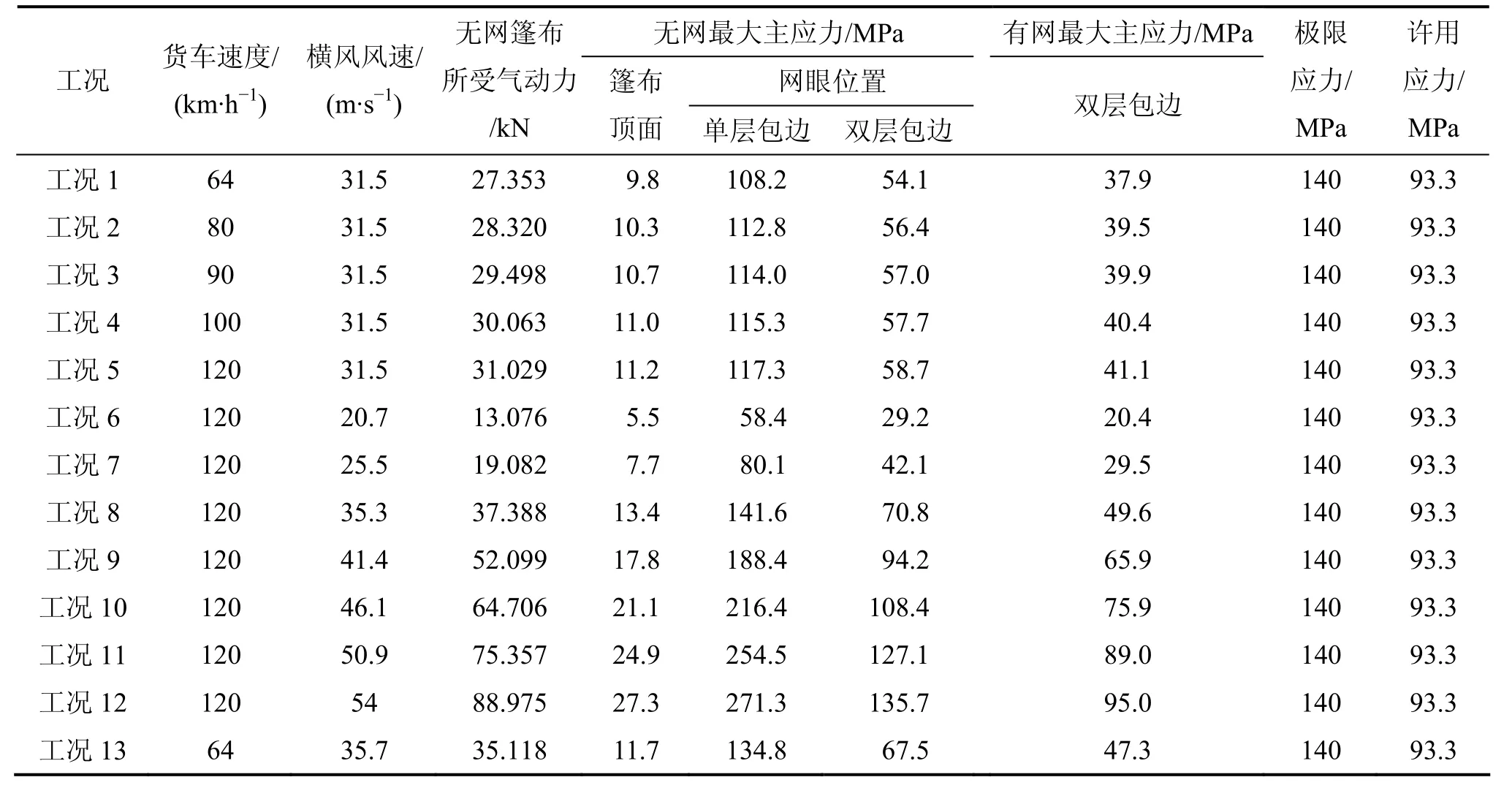
表1 不同工况下最大主应力Table 1 Maximum principle stress of tarpaulin on different operating conditions

(2) 随着货车运行速度增大，篷布顶面和篷布网眼位置的最大位移和最大主应力相应增加。

(3) 随着横风风速增大，篷布顶面和篷布网眼位置的最大位移和最大主应力随之增大。

(4) 横风风速对篷布的最大位移和最大主应力的影响大于货车速度对其的影响。

由图10可以看出：当货车速度为120 km/h、风速为31.5 m/s时，篷布顶面最大应力和最大位移分别为11.201 MPa和100.51 mm，均位于篷布的迎风面位置。篷布侧面最大应力位置位于篷布网眼位置，当网眼位置采用双层焊接结构时，网眼位置受到的最大应力为单层结构的一半。

3.3 强度校核

根据铁道部铁运(2008)60号文件中《货车 D型篷布技术条件》要求，篷布的破断拉力取为3 500 N/(50 mm)，可计算得到其极限应力为140 MPa。

参考TB 1335—78《铁路车辆强度设计及试验鉴定规范》标准，安全系数取为1.5，可得到篷布许用应力为93.3 MPa。

由实车试验结果可知：防风网能够显著降低篷布绳索拉力30%～40%，折算到篷布最大主应力相应减小30%～40%。表1所示为不同工况下有网和无网情况下篷布的最大主应力(表中有防风网数据为无网最大主应力乘以0.7)。由表1可知：

(1) 网眼位置采用双层篷布焊接结构，货车大风地区运行，横风风速小于41.4 m/s，篷布未苫盖防风网时的最大主应力小于篷布许用应力，满足篷布安全运行要求。

(2) 网眼位置采用双层篷布焊接结构，货车大风地区运行，横风风速小于54 m/s，篷布苫盖防风网时的最大主应力小于篷布许用应力，满足篷布安全运行要求。

(3) 当篷布侧面网眼位置采用双层包边结构时，篷布的最大主应力降低一半。

4 结论

(1) 网眼位置采用双层篷布焊接结构，货车大风地区运行，横风风速小于41.4 m/s，篷布未苫盖防风网时的最大主应力小于篷布许用应力，满足篷布安全运行要求。

(2) 网眼位置采用双层篷布焊接结构，货车大风地区运行，横风风速小于54 m/s，篷布苫盖防风网时的最大主应力小于篷布许用应力，满足篷布安全运行要求。

(3) 篷布所受最大应力均发生在绳索与篷布连接的眼圈位置；篷布侧面网眼位置采用双层包边结构时，篷布的最大主应力降低一半。

(4) 货车大风地区运行时，篷布顶面和篷布网眼位置的最大位移和最大主应力随着货车运行速度增加而增大；篷布顶面和篷布网眼位置的最大位移和最大主应力随着横风风速增加而增大；横风风速对篷布最大位移和最大主应力的影响大于货车速度对其的影响。

(5) 随着泊松比和篷布绳索预张力的增大，篷布顶面最大位移和最大主应力逐渐减小。

[1] 谭晓卫. 货车篷布途中脱落的原因和防范[J]. 铁道货运,2003(3): 18−19.TAN Xiao-wei. Reasons and prevention of freight tarpaulin in shedding on route[J]. Railway Freight Transport, 2003(3):18−19.

[2] 黄胜利. 浅谈列车篷布脱落问题[J]. 铁道货运, 1998(4):35−36.HUANG Sheng-li. Elementary introduction about the fall out of the railway tarpaulin[J]. Railway Freight Transport, 1998(4):35−36.

[3] 杜浙泉. 篷布绳危害列车运行安全的实例及防范[J].铁道运输与经济, 1992(1): 10.DU Zhe-quan. Examples and preventive measures on the harm of train operation safety caused by the tarpaulin rope[J]. Railway Transport and Economy, 1992(1): 10.

[4] 刘堂红, 田红旗, 梁习锋. “长白山”高速列车与货车交会试验研究[J]. 中国铁道科学, 2006, 27(3): 56−61.LIU Tang-Hong, TIAN Hong-qi, LIANG Xi-feng. Test research on Changbaishan high-speed train passing by freight car[J].China Railway Science, 2006, 27(3): 56−61.

[5] 梁习锋, 胡哲龙, 刘堂红. 集装箱专用平车气动性能分析与比较[J]. 中南大学学报: 自然科学版, 2008, 39(4): 781−786.LIANG Xi-feng, HU Zhen-long, LIU Tang-Hong. Analysis and coMParison of aerodynamic performance of container flat wagon[J]. Journal of Central South University: Science and Technology, 2008, 39(4): 781−786.

[6] 何华, 田红旗, 熊小慧, 等. 横风作用下敞车的气动性能研究[J]. 中国铁道科学, 2006, 27(3): 73−78.HE Hua, TIAN Hong-qi, XIONG Xiao-hui, et al. Study on the aerodynamics performance of gondola car under cross wind[J].China Railway Science, 2006, 27(3): 73−78.

[7] 梁习锋, 熊小慧, 易仕和. 强侧风作用下棚车气动外形优化研究[J]. 国防科技大学报, 2006, 28(2): 26−30.LIANG Xi-feng, XIONG Xiao-hui, YI Shi-he. Optimization research on aerodynamic figure of the box car under crosswinds[J]. Journal of National University of Defense Technology, 2006, 28(2): 26−30.

[8] 熊小慧, 梁习锋, 高广军, 等. 兰州-新疆线强侧风作用下车辆的气动特性[J]. 中南大学学报: 自然科学版, 2006, 37(6):1183−1188.XIONG Xiao-hui, LIANG Xi-feng, GAO Guang-jun, et al. Train aerodynamic characteristics in strong cross-wind on Lanzhou-Xinjiang railway line[J]. Journal of Central South University: Science and Technology, 2006, 37(6): 1183−1188.

[9] 田红旗. 列车空气动力学[M]. 北京: 中国铁道出版社, 2007:47−49.TIAN Hong-qi. Train aerodynamic[M]. Beijing: China Railway Publishing House, 2007: 47−49.

[10] 梁习锋, 熊小慧, 刘堂红, 等. 货车篷布、篷布绳索和篷布绳网综合试验研究总报告[R]. 长沙: 中南大学交通运输工程学院, 2009: 2−4.LIANG Xi-feng, XIONG Xiao-hui, LIU Tang-hong, et al.General report of comprehensive experimental research on freight vehicle tarpaulin, tarpaulin rope and tarpaulin nets[R].Changsha: Central South University. School of Traffic and Transportation Engineering, 2009: 2−4.

[11] 刘凤华. 不同类型挡风墙对列车运行安全防护效果的影响[J].中南大学学报: 自然科学版, 2006, 37(1): 166−182.LIU Feng-hua. Wind–proof effect of different kinds of wind-break walls on the security of trains[J]. Journal of Central South University Science and Technology, 2006, 37(1):166−182.

[12] Lien K H, Chiou Y J, Wang R Z. Vector form intrinsic finite element analysis of nonlinear behavior of steel structures exposed to fire[J]. Engineering Structures, 2010, 32(1): 80−92.

[13] Bames M R. Form-finding and analysis of prestressed nets and membranes[J]. Computer&Structures, 1998, 30(3): 149−166.

[14] Dacko A K, Glockner P G. Behaviors of spherical pneumatics subjected to axisymmetric ring loads[J]. J Non-linear Mechanics,1989, 24(4): 309−325.

[15] Zhang J Y, Ohsaki M, Kanno Y. A direct approach to design of geometry and forces of tensegrity systems[J]. International Journal of Solid and Structures, 2006, 43: 2260−2278.

[16] Wang D S, Gao C, Zhang W Y, et al. A brief introduction on structural design of cable-membrane roof and sun valley steel structure for Expo Axis project[J]. Spatial Structure, 2009, 15(1):59−96.