基于BP神经网络的城市时用水量分时段预测模型

向平，张蒙，张智，张南

(1. 重庆大学 三峡库区生态环境教育部重点实验室，重庆，400045；2. 重庆大学 城市建设与环境工程学院，重庆，400045；3重庆中法供水有限公司，重庆，400021)

城市时用水量的预测是供水系统优化调度决策的前提，预测精度直接影响到调度决策的可靠性和实用性。直接的时用水量预测是一种简单有效的预测方法，国内外学者主要致力于模型及算法改进方面的研究[1-7]，对时用水量影响因素分析较少，且在选择影响因素时并未深入分析各个小时和时间段的主要影响因素，具有很强的主观性[8-10]。对此本文作者分析各小时用水量影响因素，提取不同时段的主要影响因素，建立时用水量的分时段预测模型，并采用 BP神经网络进行预测。

1 主影响因素分析

城市时用水量相关的外部影响因素主要包括气候因素和社会因素2大类，气候因素主要有日最高气温(tmax)、日最低气温(tmin)、日平均气温(tave)、空气湿度和阴晴情况等，由于C市潮湿的特点，可以忽略空气湿度的影响；社会因素包括经济增长因素和日期因素等。对于时用水量预测这样的短期预测而言，在较短的研究时段内，经济增长因素是可以不考虑的。通过分析外部影响因素与城市时用水量的相关性，筛选出各时用水量的主要影响因素。通过分析 C市某片区2010年气温较高的8月份连续21 d时用水量实测数据(图1)及相应的气象资料和日期量数据(图2和表1)，得出时用水量的主要影响因素。

首先，根据阴晴量和日期量对时用水量的实际影响情况，对其进行量化，数字化对照表见表 2。表 2中阴晴量的量化根据晴天用水量较多，大雨天用水量较少的影响关系给予量化；日期量量化值通过分析C市日期对应日用水量平均值进行分析，得出其余日用水量与周一用水量的比值，即为日期量量化值。然后对时用水量(Q)、日最高气温、日最低气温、日平均气温、阴晴量(QYQ)、日期量(QRQ)序列进行相关性分析，结果见图3和表3。

图1 时用水量实测数据Fig.1 Measured hourly water consumption data

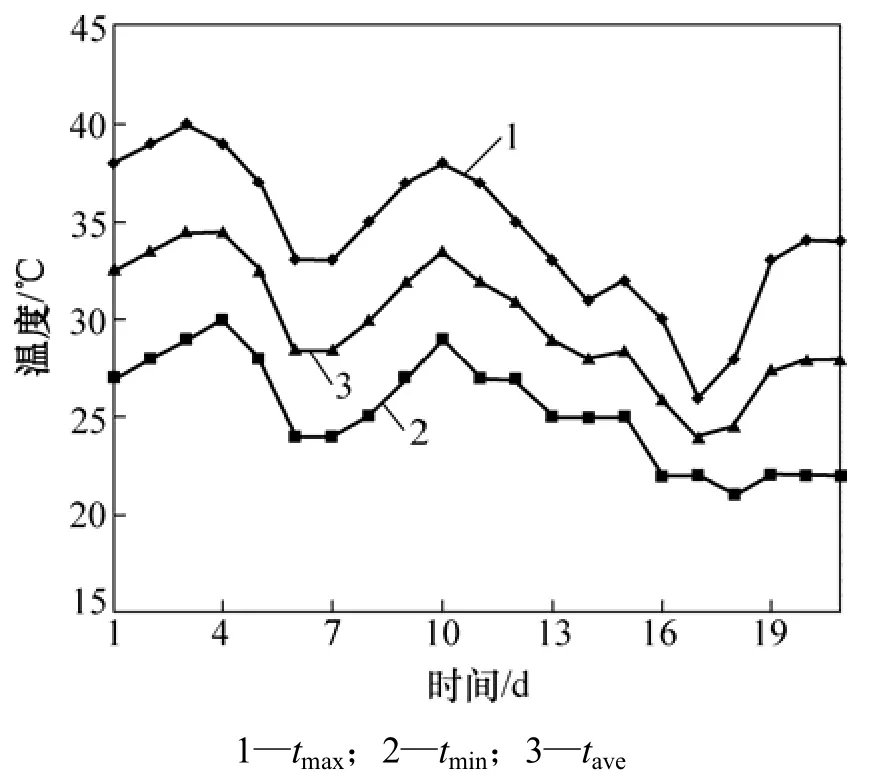
图2 气温数据Fig.2 Temperature data

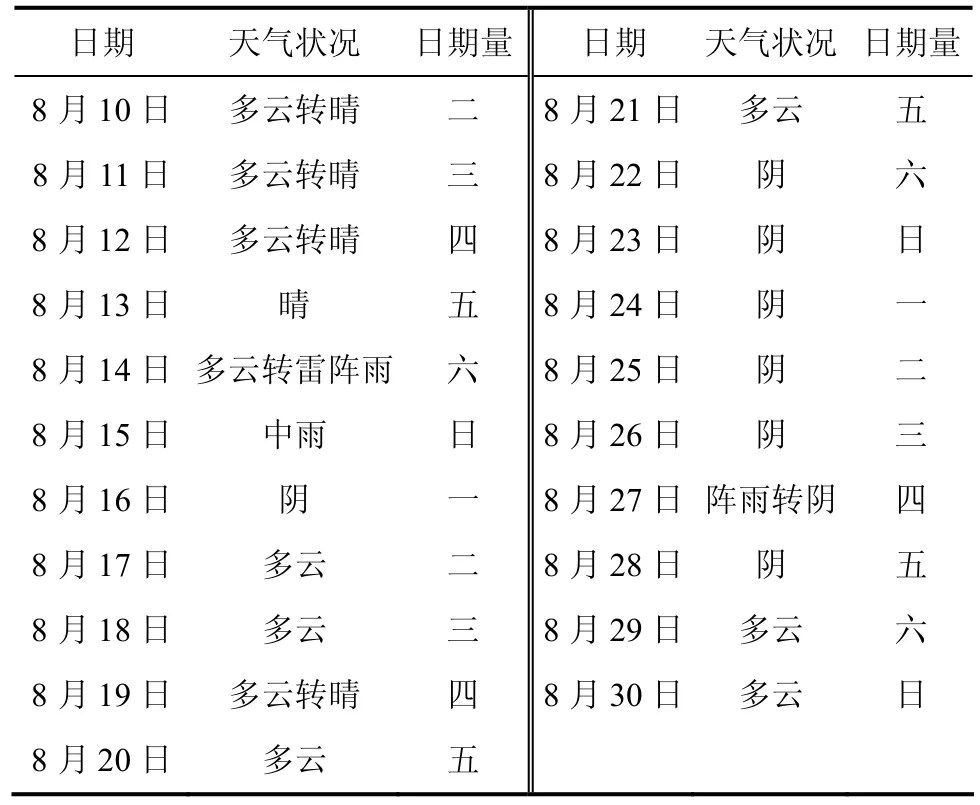
表1 天气状况及日期情况Table 1 Weather and date data

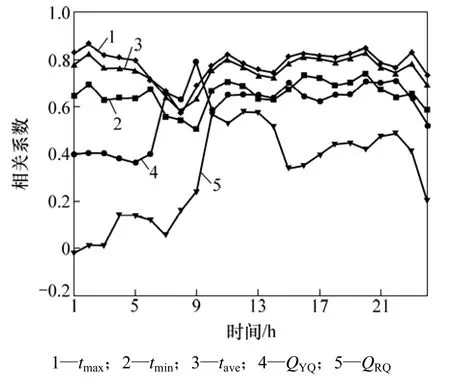
图3 时用水量与影响因素的相关系数变化Fig.3 Correlation coefficient change of water demand and its impact factors

表2 天气状况及日期量数字化对照Table 2 Comparison of weather condition and date digitalization

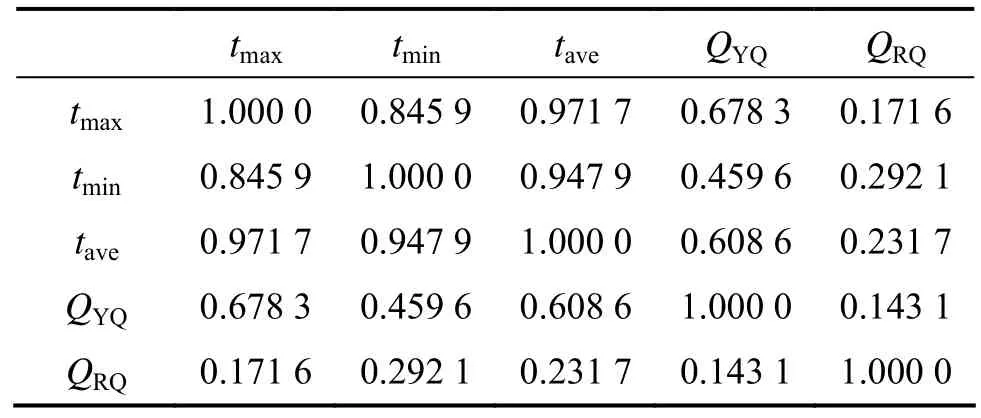
表3 影响因素之间的相关系数Table 3 Correlation coefficient between factors

从图3可以看出：时用水量与各因素均成正相关关系，且相关性由强至弱分别为 tmax，tave，tmin，QYQ和QRQ。但是从表3中可以看出：tmax，tave和tmin之间有很强的相关性，可以只考虑一种相关性最高的因素Tmax为主要因素。所以，影响时用水量的主要因素为日最高气温、阴晴量和日期量。

2 分时段用水量模型

通过分析时用水量分布特点及主要影响因素，筛分出具有相关性一致的各时段(表4)，并考虑时用水量影响的滞后性，建立分时段用水量模型(表5)。减少冗余因素的不利影响，节省运行时间且满足精度要求，对于时用水量预测是有意义的。

通过表4可以看出：时段1时用水量与日最高气温有很强的相关性(0.804 9)，而与阴晴量和日期量相关性均较弱(均小于0.4)；时段2时用水量与日最高气温和阴晴量相关性较高；时段3时用水量与最高气温、阴晴量和日期量相关性较高。所以，将调度1 d分为3个时间段分别预测是合理的。

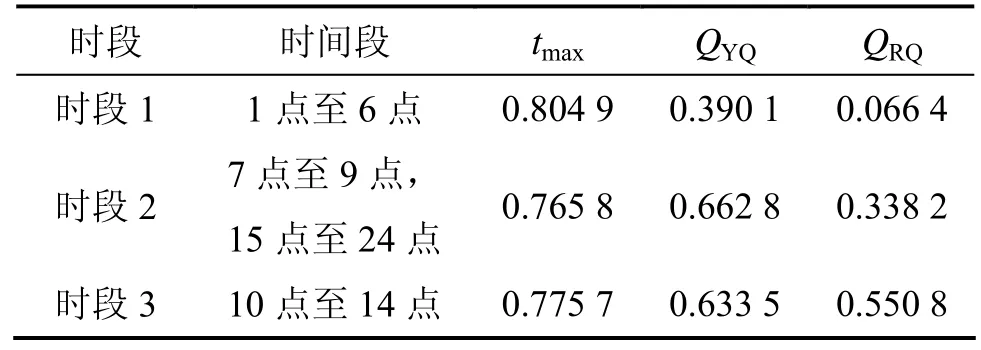
表4 各时段时用水量与主要因素之间的平均相关性系数Table 4 Average correlation coefficient between water consumption of different periods and main factors

表5 分时段用水量模型Table 5 Period-divided water consumption model

3 BP神经网络模型原理及应用

BP神经网络在用水量预测方面研究较为广泛[11-13]，它包括输入层、隐层和输出层，信息通过输入层传递到隐层的神经元上，经过各神经元作用函数运算后，把隐层神经元信息输出至输出层的神经元上输出结果。训练过程分为正向和反向传递2个过程，输入信息经隐层传递至输出层，若输出结果和期望值有误差，则将误差信息沿原网络返回，通过修改神经元的权值，在经过正向传递过程，反复循环直至达到要求。若输入层有r个输入量[P1，P2，Pr]，隐含层和输出层神经元数分别为S1和S2，隐含层和输出层的激活函数分别为f1和f2。

则隐层第i个神经元的输出为：

隐层的输出为输出层的输入，输出层第k个神经元的输出为：

输出层权值变化：

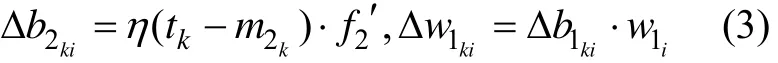
隐含层权值变化：

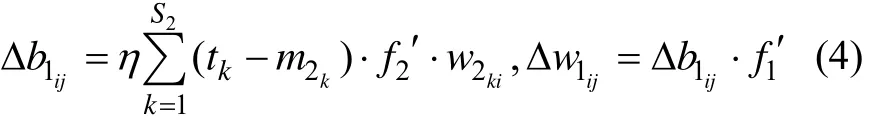
根据 BP神经网络预测原理和预测目的，确定输入单元数和输出单元数。在设计BP网络中，应优先考虑3层BP网络(即1个隐层)[14]。一般地，靠增加隐层节点数来获得较低的误差，其训练效果要比增加隐层数更容易实现。研究表明，3层神经网络在其隐层中使用S型传输函数，在输出层中使用线性传输函数，可以任意精度逼近任意函数[15]。网络训练中样本容量应足够大，同时为了避免陷入过度训练状态，样本容量不宜过大。隐层节点数必须小于(训练样本-1)，训练样本数必须多余网络模型的连接权数，一般为2～10倍。本文基于Matlab工具平台，采用“尝试法”确定网络训练函数和隐层神经元数。对网络分别训练50次，最后根据计算平均绝对百分比误差(MAPE)，检验预测结果是否满足精度要求。

3.1 模型设计

模型设计对照见表6。

3.2 模型结果比较

从图4可以看出：该模型预测用水量与实测值拟合较好。从图5 可看出：残差序列中最大残差为482.33 m3/h，最大误差为4.67%，满足调度5%的精度要求。从表7可以看出：各时段的MAPE均较小(1%左右)，说明模型精度均较高。

图4 预测值与实际值比较Fig.4 Comparison of predicted values and actual values

表6 模型设计对照Table 6 Model design comparison table

图5 预测残差变化曲线Fig.5 Prediction residual sequence curve

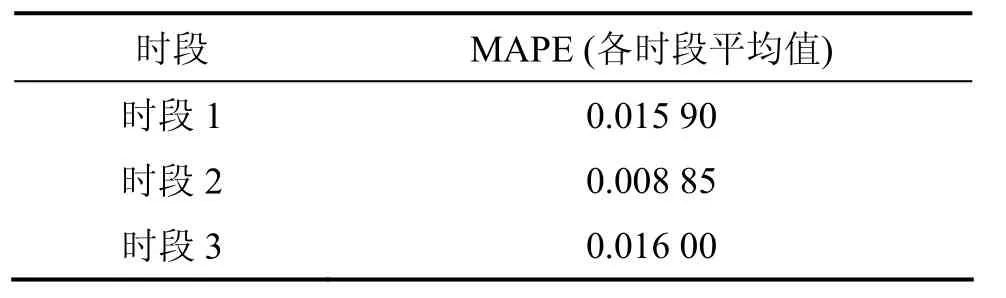
表7 模型结果MAPE值Table 7 MAPE value of model results

4 结论

(1) 通过对 C市各时段用水量与影响因素之间的相关性分析，进行因素筛选，得出每日3个时段的主要影响因素，分别为日最高气温、阴晴量和日期量，每个城市不同时节每天各个时段的影响因素有所差别，需要具体问题具体分析，因此避免冗余因素的不利影响是有意义且必要的。

(2) 通过C市时用水量影响因素筛选，建立时用水量分时段模型，各时段神经网络结果神经元数分别为7，9，11，有效简化部分网络结构，避免了网络结构复杂造成的诸如“过饱和”现象，并且预测精度仍然达到要求。模型计算结果MAPE均在5%范围内，表明各时段BP网络预测结果的精度满足要求。

(3) 城市时用水量属于短期预测，据预测时间越近的数据结果影响越大，实际工程中要不断更新数据。

[1] Herrera M, Torgo L, Izquierdo J, et al. Predictive models for forecasting hourly urban water demand[J]. Journal of Hydrology,2010, 387(1/2): 141-150.

[2] Alvisi S, Franchini M, Marinelli A. A short-term, pattern-based model for water-demand forecasting[J]. Journal of Hydroinformatics, 2007, 9(1): 39-50.

[3] Ashu J, Ashish K V, Umesh C J. Short-term water demand forecast modeling at IIT Kanpur using artificial neural networks[J]. IEE Transactions on Water Resources Management,2001, 15(1): 299-321.

[4] 俞亭超, 张土桥, 柳景青. 峰值识别的 SVM模型及在时用水量预测中的应用[J]. 系统工程理论与实践, 2005, 25(1):134-137.YU Ting-chao, ZHANG Tu-qiao, LIU Jing-qing. SVM model with peak value recognition and its application to hourly water consumption forecasting[J]. System Engineering-Theory &Practice, 2005, 25(1): 134-137.

[5] 王亮, 张宏伟, 牛志广. 支持向量机在城市用水量短期预测中的应用[J]. 天津大学学报, 2005, 38(11): 1021-1025.WANG Liang, ZHANG Hong-wei, NIU Zhi-guang. Application of support vector machines in short-time prediction of urban water consumption[J]. Journal of Tianjin University, 2005,38(11): 1021-1025.

[6] 刘洪波, 张宏伟, 闫静静. 基于模糊聚类理论的水量短期预测方法[J]. 哈尔滨工业大学学报, 2009, 41(12): 162-165.LIU Hong-bo, ZHANG Hong-wei, YAN Jing-jing. Short-term load forecasting technique for municipal supply water consumption based on fuzzy clustering theory[J]. Journal of Harbin Institute of Technology, 2009, 41(12): 162-165.

[7] 陈磊. 基于遗传支持向量机的时用水量预测模型[J]. 沈阳工业大学学报, 2010, 32(5): 555-578.CHEN Lei. Forecasting model for hourly water consumption using genetic algorithm based support vector machine[J]. Journal of Shenyang University of Technology, 2010, 32(5): 555-578.

[8] 周天佐. 城市供水系统优化调度的研究[D]. 长沙: 中南大学交通系统工程与控制研究所, 2009: 26-32.ZHOU Tian-zuo. Research on optimal operation of urban water supply system. Nanjing[D]. Changsha: Central South University.Transportation Systems Engineering and Control Research Institute, 2009: 26-32.

[9] 陈卫, 陆建, 吴志成. BP网络的城市时用水量预测组合模型[J]. 哈尔滨工业大学学报, 2009, 41(6): 197-200.CHEN Wei, LU Jian, WU Zhi-cheng. Combined forecast model of urban hourly water consumption based on BP neural network[J]. Journal of Harbin Institute of Technology, 2009,41(6): 197-200.

[10] Narate L, Chridtine W C. A toolset for construction of hybrid intelligent of recasting systems: Application of water demand Prediction[J]. Artificial Intelligence in Engineering, 1999, 13(1):21-42.

[11] 乔伟德. 基于遗传神经网络的城市用水量预测研究[J]. 水科学与工程技术, 2007(3): 1-3.QIAO Wei-de. Research on urban water demand prediction based on genetic-neural network[J]. Water Sciences and Engineering Technology, 2007(3): 1-3.

[12] Ghiassi M, Zimbra D K, Saidane H. Urban water demand forecasting with a dynamic artificial neural net-work model[J].Journal of Water Resources Planning and Management, 2008,134(2): 138-146.

[13] 王亮, 张宏伟, 岳琳, 等. PSO-BP模型在城市用水量短期预测中的应用[J]. 系统工程理论与实践, 2007(9): 156-170.WANG Liang, ZHANG Hong-wei, YUE Lin, et al. Application of PSO-BP model in short-term prediction of urban water demand[J]. Systems Engineering Theory & Practice, 2007(9):156-170.

[14] 周开利, 康耀红. 神经网络模型及其MATLAB仿真程序设计[M]. 北京: 清华大学出版社, 2005: 11-14.ZHOU Kai-li, KANG Yao-hong. Neural network model and its MATLAB simulation programming design[M]. Beijing: Qinghua University Press, 2005: 11-14.

[15] 单金林, 戴雄奇, 李江涛. 利用BP网络建立预测城市用水量模型[J]. 中国给水排水, 2001, 17(8): 61-63.SHAN Jin-lin, DAI Xiong-qi, LI Jiang-tao. BP neural network method for predicting urban water consumption[J]. China Water＆Wastewater, 2001, 17(8): 61-63.