山区大跨径中承式钢管混凝土拱桥主拱线型比较分析
张贤霂, 刘 伟
(四川省交通勘察设计研究院有限公司,四川成都 610017)
1 工程概况
某高速公路特大桥跨越“V”形河沟而设,结合地质、地形、岸坡稳定条件及景观要求,采用360 m中承式钢管混凝土拱桥,桥梁采用整幅设计,全桥总长389.6 m。拱肋为变截面钢管混凝土桁架结构,净跨径为360 m,计算矢跨比为l/4.5,拱轴系数为1.45,拱顶截面径向高为6.5 m,拱脚截面径向高为12.0 m,肋宽为4.0 m,拱肋中心距为33.0 m;每肋为上、下各两根φ1300×40/36/30/26/22 mm,横向通过φ762×16 mm横联钢管连接,竖向通过φ660×12 mm腹杆钢管连接而构成。拱肋φ1300 mm弦管内灌C60自密实补偿收缩混凝土,为加强拱肋横向连接,吊杆处上横联灌注C60自密实补偿收缩混凝土。
桥面系采用钢格子梁的钢-混凝土组合梁。标准段桥面钢格子梁由两道边纵梁(吊杆处)、三道中纵梁与吊杆处的主横梁及三道次横梁组成;钢格子梁均采用“工”形截面。预制桥面板采用等厚,厚度为22 cm,预制桥面板通过湿接缝和纵横梁剪力钉连接形成一个整体(图1)。

图1 桥梁立面布置(单位:cm)
2 有限元模型
结构计算采用midas2019进行空间计算,材料按线弹性计。拱肋、格子梁、立柱等采用梁单元模拟,吊杆采用桁架单元模拟,桥面板采用梁单元模拟;拱脚处固结,并采用弹性连接模拟各处支座(图2)。
图2 桥梁有限元模型
3 主拱线型比较分析
3.1 矢跨比
根据JTG/T D65-06-2015《公路钢管混凝土拱桥设计规范》第8.1.2条,对于中承式钢管混凝土拱桥,主拱矢跨比取值范围宜为:1/3.5~1/5,结合本桥实际,取矢跨比分别为1/4、1/4.5、1/5三种进行分析对比。
3.1.1 结构内力
在恒载作用下主拱上、下弦弯矩图如下图所示(取拱轴系数为1.45),限于图幅,仅示意半跨计算结果(图3、图4)。
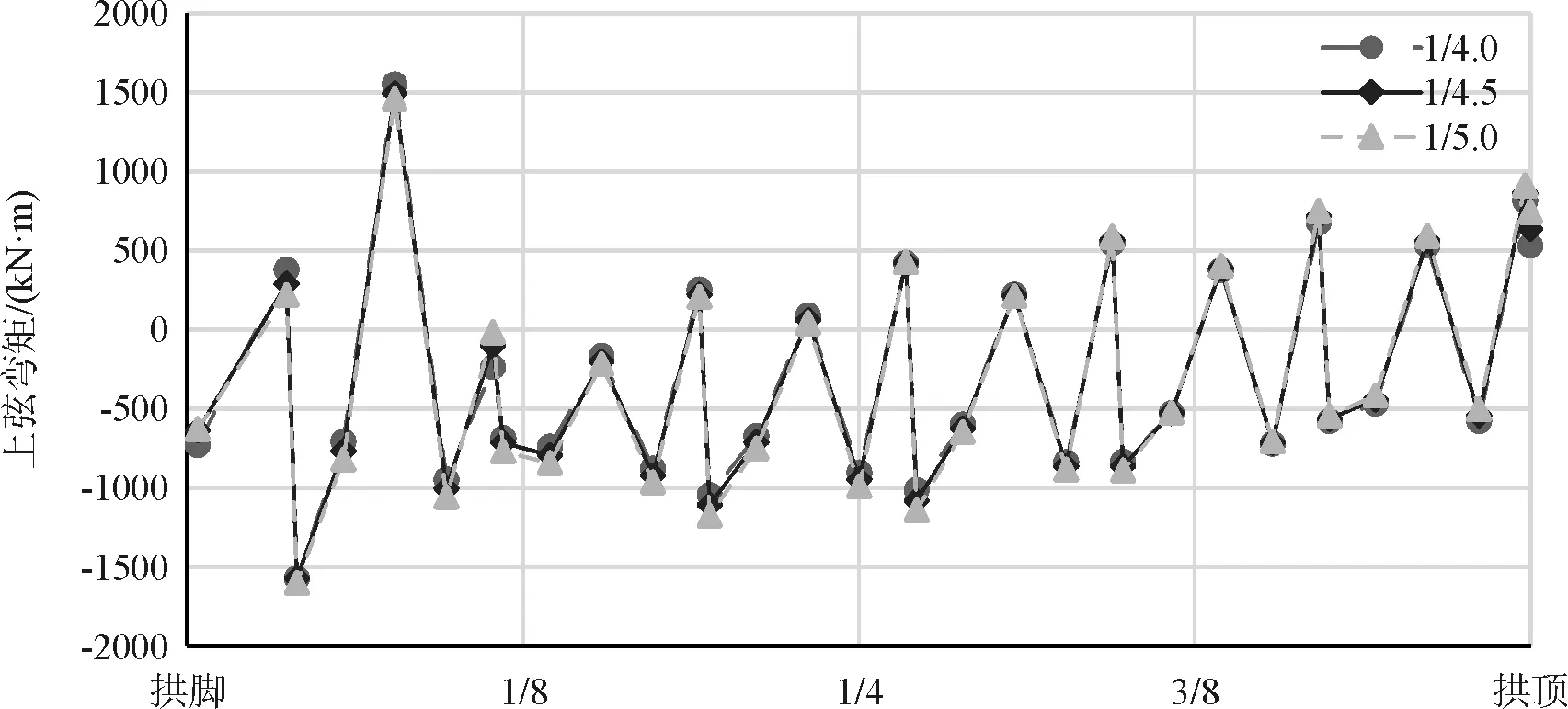
图3 不同矢跨比下主拱上弦弯矩

图4 不同矢跨比下主拱下弦弯矩
通过上两图对比分析可知,在拱轴系数均为1.45时,不同矢跨比下,主拱上、下弦弯矩差异较小,即矢跨比对主拱上、下弦弯矩影响较小。
在恒载作用下主拱上、下弦轴力、轴力差如图5~图7所示。
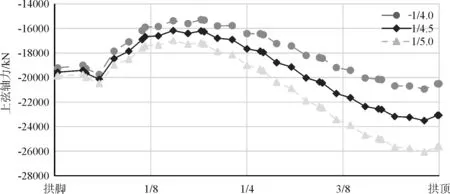
图5 不同矢跨比下主拱上弦轴力

图6 不同矢跨比下主拱下弦轴力

图7 不同矢跨比下主拱上、下弦轴力差(绝对值)
通过上图对比分析可知,在拱轴系数均为1.45时,主拱上弦轴力随着矢跨比增加而减小,最大轴力在拱顶;主拱下弦轴力随着矢跨比增加也减小,但最大轴力在拱脚;矢跨比为1/4时,主拱上、下弦轴力整体水平显著小于另外两种情况,特别是拱顶上弦轴力,较矢跨比1/5小了接近5 100 kN,占比20 %,差异幅度较大,且此时主拱上、下弦轴力差值最小,说明整体截面弯矩也最小,故矢跨比1/4的方案较其它方案优。
3.1.2 结构变形
在恒载+活载作用下主拱竖向变形如图8所示(取拱轴系数为1.45),限于图幅,仅示意半跨计算结果。
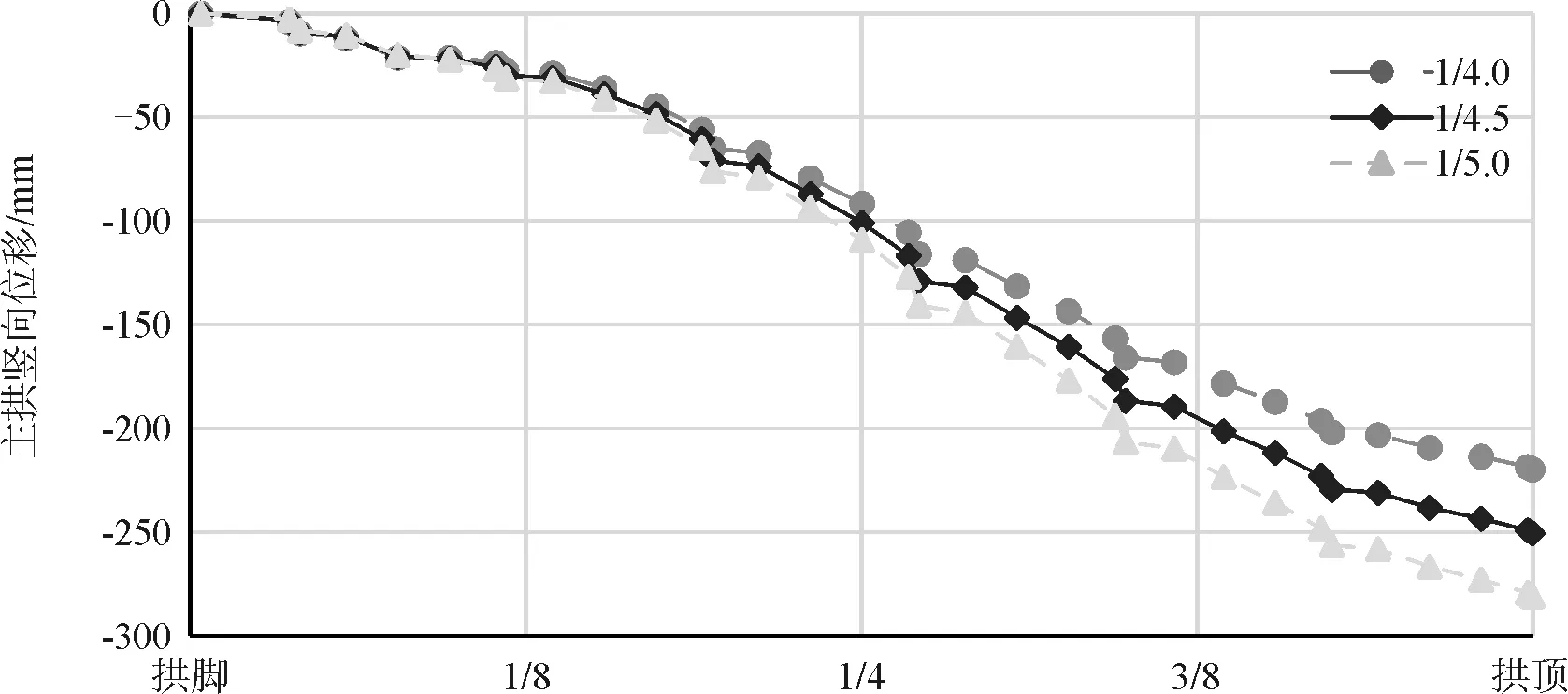
图8 不同矢跨比下主拱竖向变形
通过上图可知,主拱竖向变形随着矢跨比增加而减小,矢跨比1/4时,拱顶竖向变形为220 mm,小于矢跨比1/4.5时的249 mm与矢跨比1/5时的279 mm。从变形角度,矢跨比1/4方案较优。
3.2 拱轴系数
根据JTG/T D65-06-2015《公路钢管混凝土拱桥设计规范》第8.1.2条,对于中承式悬链线钢管混凝土拱桥,主拱拱轴系数不宜大于1.9,结合本桥实际,取拱轴系数分别为1.25、1.35、1.45、1.55、1.65、1.75六种进行分析对比。
3.2.1 结构内力
对于不同拱轴系数,在恒载作用下主拱上、下弦弯矩如图9、图10所示(矢跨比1/4.5),限于图幅,仅示意半跨计算结果。
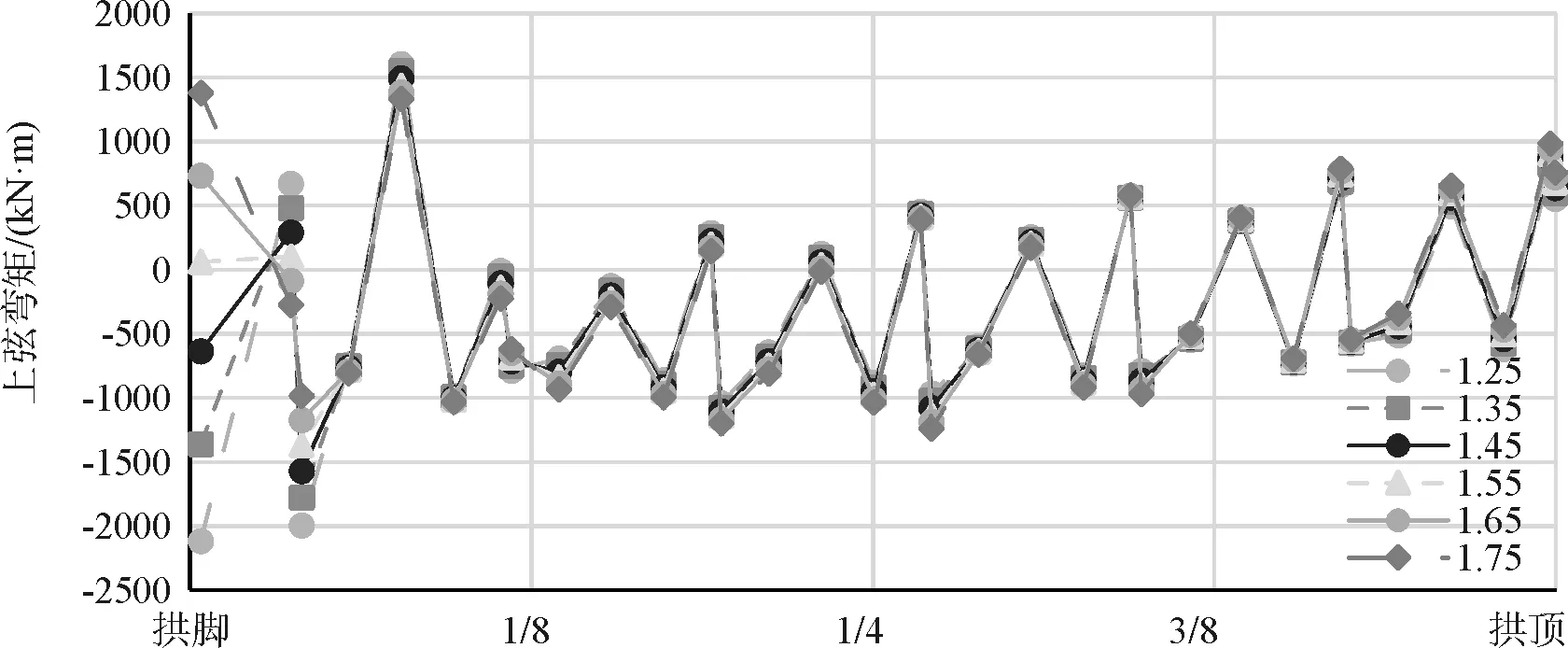
图9 不同拱轴系数下主拱上弦弯矩

图10 不同拱轴系数下主拱下弦弯矩
通过上图对比分析,在不同拱轴系数(1.25、1.35、1.45、1.55、1.65、1.75)下,主拱上、下弦弯矩值除拱脚及附近位置外,其余位置差异均较小;在拱脚处,随着拱轴系数由1.25变化至1.45,弯矩绝对值逐渐减小;而随着拱轴系数由1.55变化至1.75,弯矩绝对值又逐渐增大;因此为使主拱弯矩在绝对值在整个主拱范围内较小且均匀,取拱轴系数为1.45、1.55较合适。
对于不同拱轴系数,在恒载作用下主拱上、下弦轴力及轴力差如图11~图13所示。
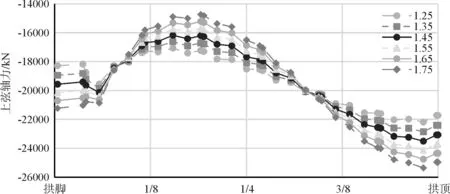
图11 不同拱轴系数下主拱上弦轴力
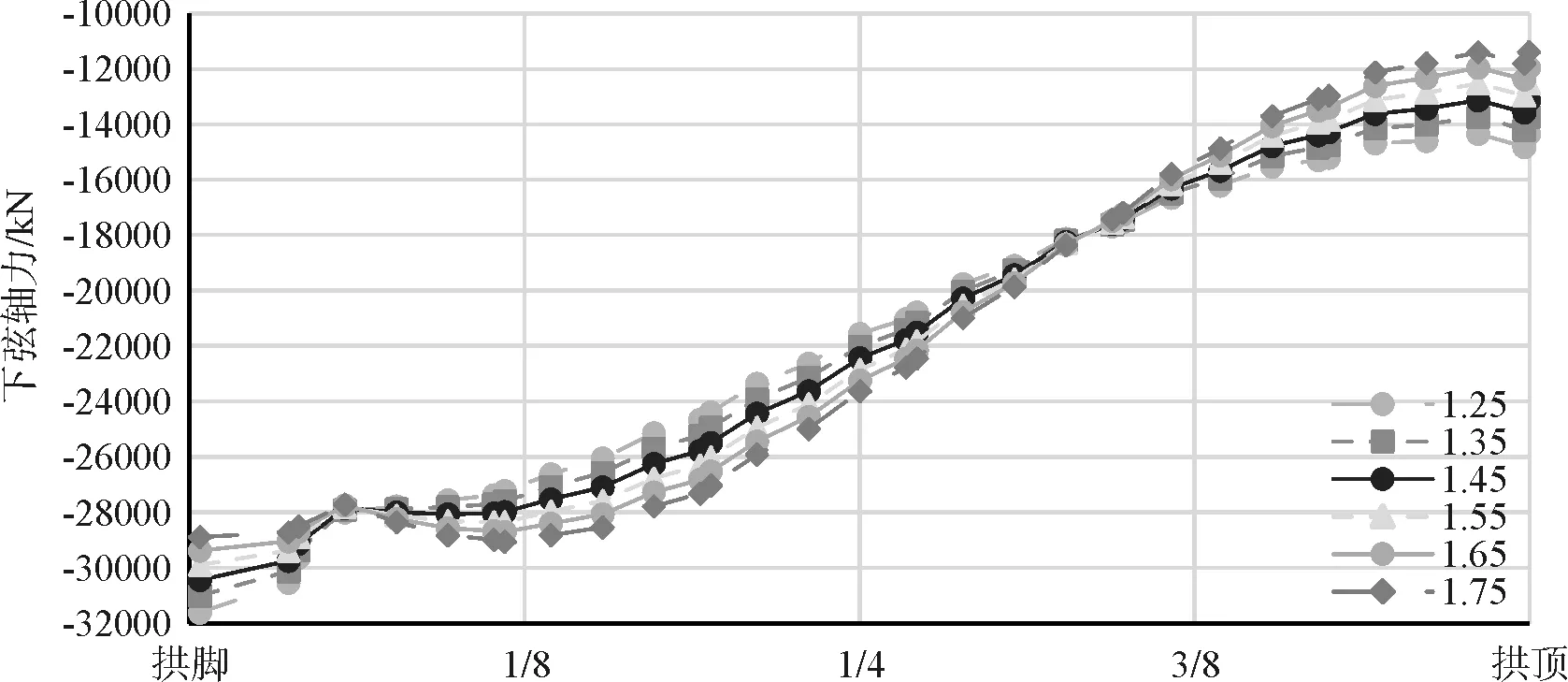
图12 不同拱轴系数下主拱下弦轴力

图13 不同拱轴系数下主拱上、下弦轴力差(绝对值)
通过图11、图12对比分析,对于上弦,拱脚处轴力随着拱轴系数增加而增大,主拱1/8截面处轴力随着拱轴系数增加而减小,拱顶处轴力随着拱轴系数增加而增大;对于下弦,拱脚处轴力随着拱轴系数增加而减小,主拱1/8截面处轴力随着拱轴系数增加而增大,拱顶处轴力随着拱轴系数增加而减小。同时由图13可知,拱脚处上、下弦轴力差随着拱轴系数增加而减小,主拱1/8截面处上、下弦轴力差随着拱轴系数增加而增大,拱顶处上、下弦轴力差随着拱轴系数增加而增大。由上述三图则可以明显看出,拱轴系数1.45对应的上、下弦轴力及轴力差变化曲线均位于所有曲线中间,说明此拱轴系数时,上、下弦轴力及轴力差在整个主拱范围内分布较为均匀、适中。从轴力角度看,拱轴系数1.45较为合适。
3.2.2 结构变形
对于不同拱轴系数,在恒载+活载作用下主拱竖向变形如图14所示(矢跨比1/4.5)。

图14 不同拱轴系数下主拱竖向变形
通过图14可知,1/8、1/4截面处主拱竖向变形随着拱轴系数增加而减小,3/8、拱顶处主拱竖向变形随着拱轴系数增加而增大。拱轴系数为1.25时,3/8、拱顶截面处竖向变形最小,1/8、1/4截面处竖向变形最大;拱轴系数为1.75时,3/8、拱顶截面处竖向变形最大,1/8、1/4截面处竖向变形最小;拱轴系数为1.45时,竖向变形均位于居中水平。从变形角度看,拱轴系数为1.25时,主拱竖向刚度最大,为最优方案。
4 结论
通过以上分析主要得出以下结论:
(1)恒载作用下,矢跨比对主拱上、下弦弯矩影响较小,对上、下弦轴力及轴力差影响较大。上、下弦轴力及轴力差均随着矢跨比增加而减小,从内力角度看,矢跨比取1/4较合适。
(2)在恒载+活载作用下,主拱竖向变形随着矢跨比增加而减小,矢跨比1/4时主拱竖向刚度最大,变形最小。
(3)从结构内力与变形来看,矢跨比1/4方案优于其它方案,但矢跨比选择还需要考虑景观、经济性方面的因素。对山区大跨径拱桥,两岸接线标高影响桥面位置,而桥位地形、地质、岸坡稳定条件决定拱座基础位置,受上述因素影响,本桥拱座位置较高,距桥面较近,虽为中承式拱桥,实则更接近下承式的立面效果。若采用矢跨比为1/4方案,则桥面以上主拱高度较大,视觉稳定性较差且显得沉重,景观效果较差,同时主拱用钢量也较大,经济性较差。故综合考虑结构受力、景观效果及经济性,本桥主拱矢跨比采用1/4.5。
(4)恒载作用下,拱轴系数仅对拱脚及附近位置的主拱上、下弦弯矩影响较大,其余位置影响较小。在拱脚处,随着拱轴系数由1.25变化至1.45,弯矩绝对值逐渐减小;而随着拱轴系数由1.55变化至1.75,弯矩绝对值又逐渐增大。从弯矩角度看,拱轴系数1.45、1.55较合适。
(5)恒载作用下,拱轴系数对上、下弦轴力及轴力差影响较大,随着拱轴系数增大,主拱不同位置的上、下弦轴力及轴力差表现出或增或减的不同变化规律,而拱轴系数1.45的变化曲线适中位于所有曲线中间,说明此拱轴系数时,上、下弦轴力及轴力差在整个主拱范围内分布较为均匀、适中。故基于轴力考虑,拱轴系数选取1.45较为合适。
(6)在恒载+活载作用下,1/8、1/4截面处主拱竖向变形随着拱轴系数增加而减小,3/8、拱顶处主拱竖向变形随着拱轴系数增加而增大。拱轴系数为1.25时,拱顶竖向变形最小,主拱竖向刚度最大。
(7)综合对比主拱轴力、弯矩及变形分析结果,本桥拱轴系数取为1.45较为合适。

