轴向运动黏弹性Timoshenko 梁横向非线性强受迫振动
李 彪,唐有绮,丁 虎,陈立群,3
(1.上海卫星工程研究所,上海 200240;2.上海大学 上海市应用数学和力学研究所,上海 200072;3.上海大学 力学系,上海 200444)
动力传送带、磁带、纸带、带锯、空中缆车索道、高楼升降机缆绳、单索架空索道等多种工程系统元件,都可模型化为轴向运动梁。尽管以上的工程系统元件各有各的特点和用途,但与其运动方向垂直的横向振动会在一定程度上限制这些元件的效用。研究轴向运动梁横向振动机理对优化设计工程系统元件至关重要。分析轴向运动梁横向运动工程意义重大,因此,更广受关注[1-3]。
Mote[4]用Galerkin截断法研究了两端铰支 Euler梁的固有频率。Simpson[5]利用本征值方法研究了轴向运动梁在固定边界条件下的固有频率和模态函数,但未考虑轴向初始张力。杨晓东等[6]研究了两端带有相同刚度扭转弹簧铰支的轴向运动梁横向振动问题。丁虎等[7]研究了这种混杂边界情况下轴向变速梁的横向振动稳定性。
以上模型均采用欧拉梁模型。Ghayesh等[8]研究了轴向运动Timoshenko梁非线性参数振动和稳定性。Lee等[9]应用谱分析的方法研究了轴向运动Timoshenko梁,通过与传统的有限元解和精确解析解的对比,验证了谱单元法高精确度。Tang等[10-11]研究了轴向运动Timoshenko梁的受迫振动和参激振动。但所有关于轴向运动Timoshenko梁的研究都未考虑黏弹性的影响,而实际工程中的黏弹性阻尼总是存在且不能忽略的。因此对轴向运动黏弹性Timoshenko梁的横向振动的研究是很有必要的,而这正是本文研究的目标。
1 数学模型
考虑轴向运动黏弹性Timoshenko梁,密度为ρ,截面面积为A,截面绕中性轴转动惯量为J,弹性模量为E,轴力为P(x,t),剪切模量为G。梁以速度Γ运动,两端长度为L。y为梁轴线在X处的横向位移,Ψ(x,t)为弯矩产生的梁轴线(忽略剪切变形时)转角。轴向运动梁的物理模型如图1所示。
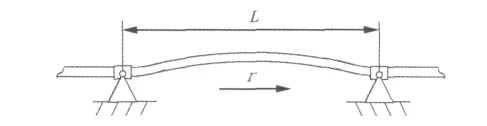
图1 Timoshenko梁物理模型Fig.1 The physical model of a Timoshenko beam
系统的总动能T与势能U分别为:
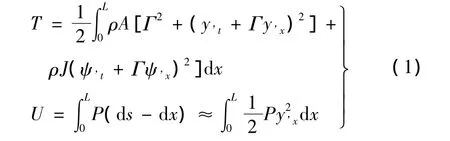
变形功的变分δWd为:
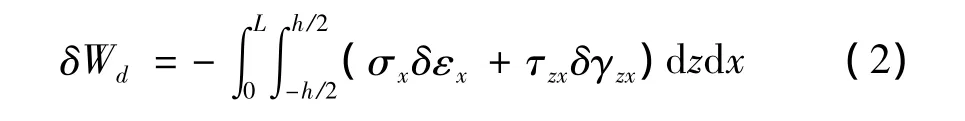
黏弹性本构关系为Kelvin模型并取物质时间导数:
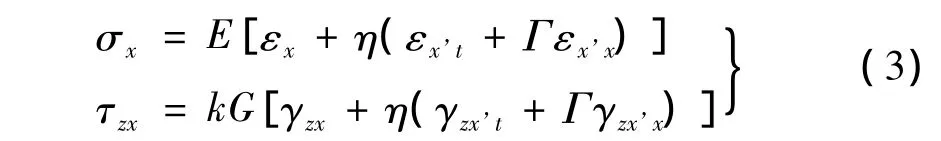
由外力引起的有用功的变分为:
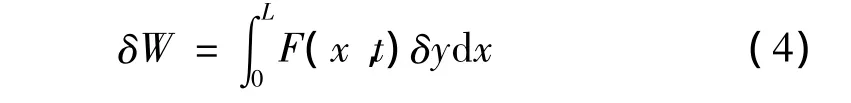
式中:F=F0cos(ωt)为分布的面载荷,F0,ω分别为外力幅值与频率。当外激励足够大时,可将其作强受迫振动处理。广义哈密尔顿原理为:
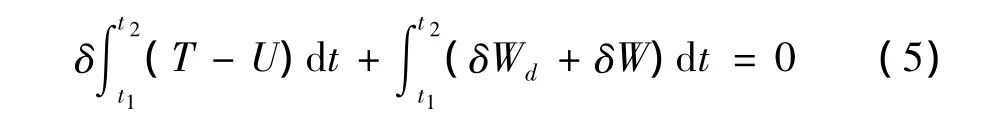
引入无量纲参数:
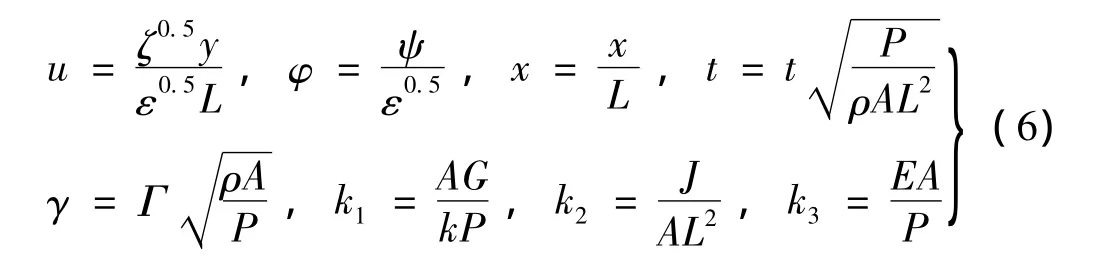
ε为无量纲参数,表示横向位移、转角以及Timoshenko梁的黏弹性系数均为小量。用 ζ表征非线性系数。
运动梁微分方程及边界条件无量纲形式为:
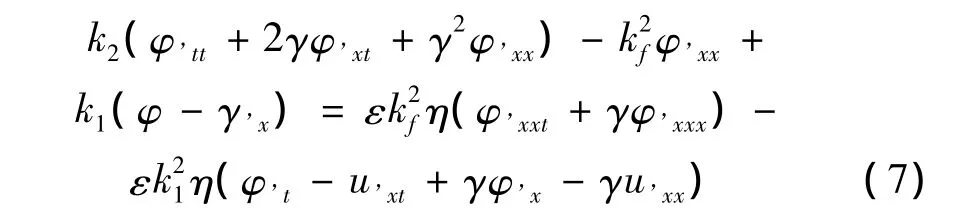
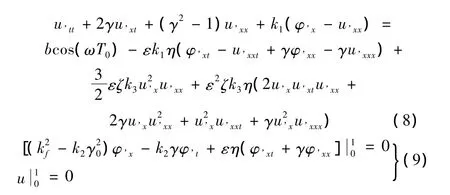
2 多尺度分析及幅频响应
对式(7)、式(8)应用直接多尺度方法,设其近似解为:
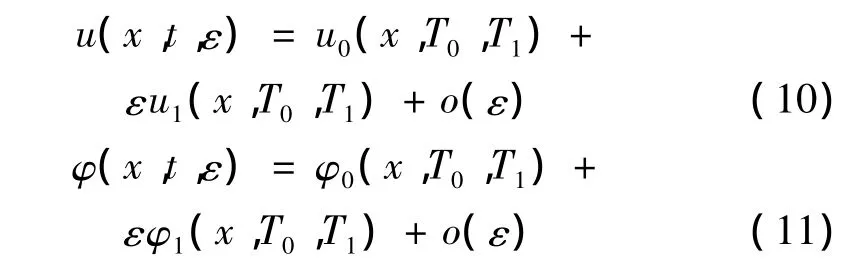
式中:T0=t和T1=εt分别为快时间和慢时间尺度。将式(10)、式(11)代入式(7)、式(8),分离 ε0,ε1不同阶量,得:
ε0阶为:
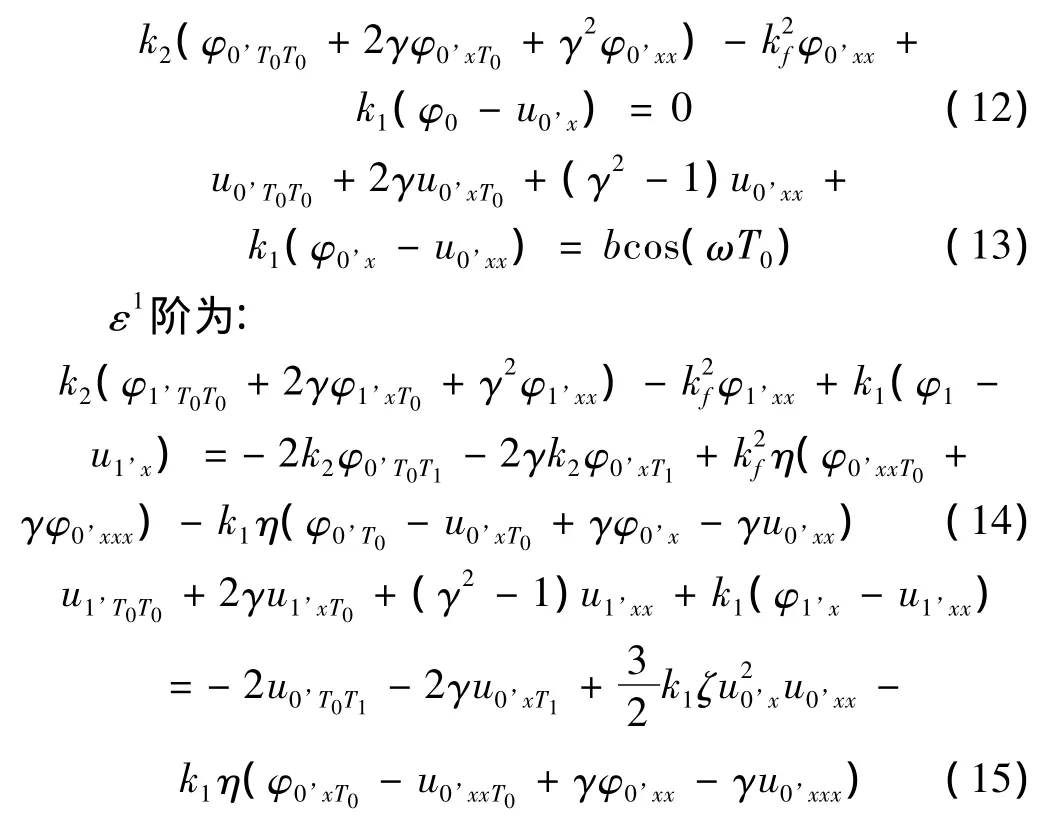
式(12)、(13)解耦简化为:
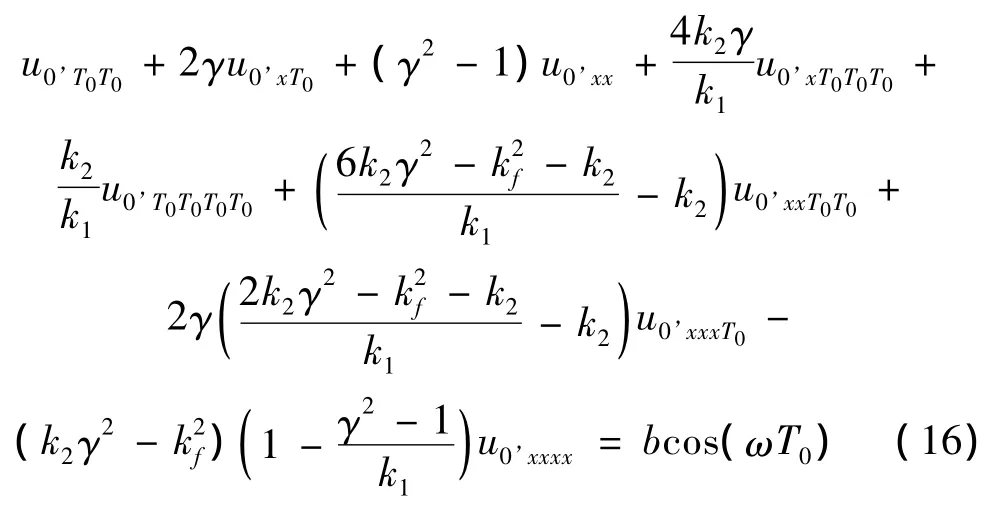
式(16)的解为:
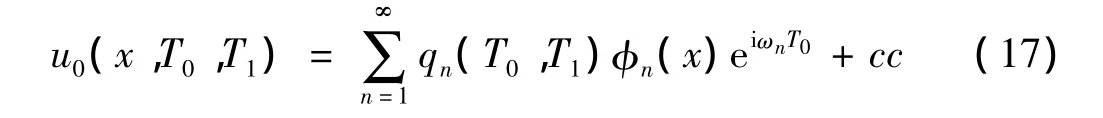
其中qn(T0,T1)为 T0和 T1的函数,式(17)代入式(16),两端同乘 φ(x)并在[0,1]上积分:
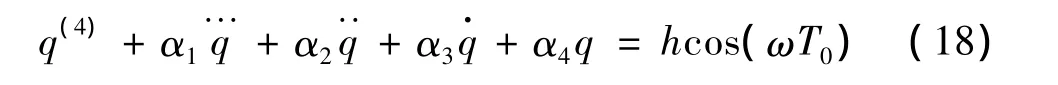
其中:q为式(18)的解,设:
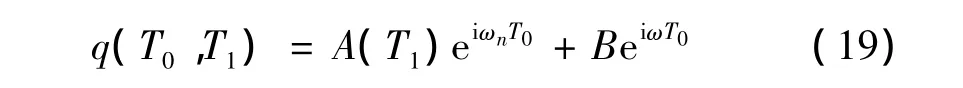
将式(19)代入式(18),得:
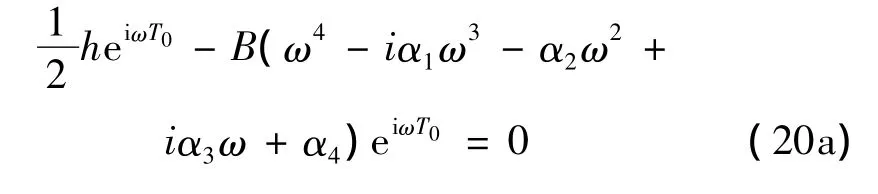
其中:

可得B值为:
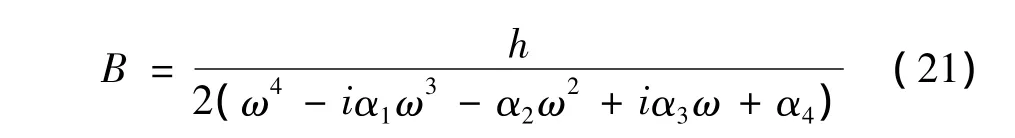
线性派生系统式(12)、式(13)的固有频率及模态已由文献[12]给出。外激力频率接近系统固有频率三分之一时,超谐波共振可能产生。为分析共振点附近的响应,引入简谐参数σ表示扰动频率ω与固有频率ωn的关系:
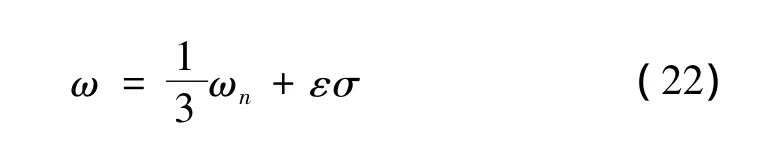
式中:ωn为系统式(12)、式(13)的第n阶固有频率。假设式(14)、式(15)的解为:
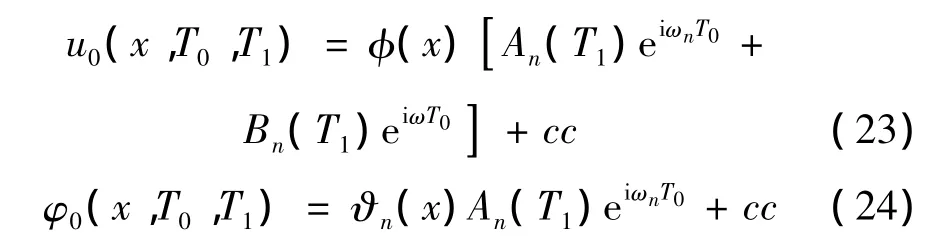
将式(22),式(23)和式(24)代入式(14)和式(15)得到:
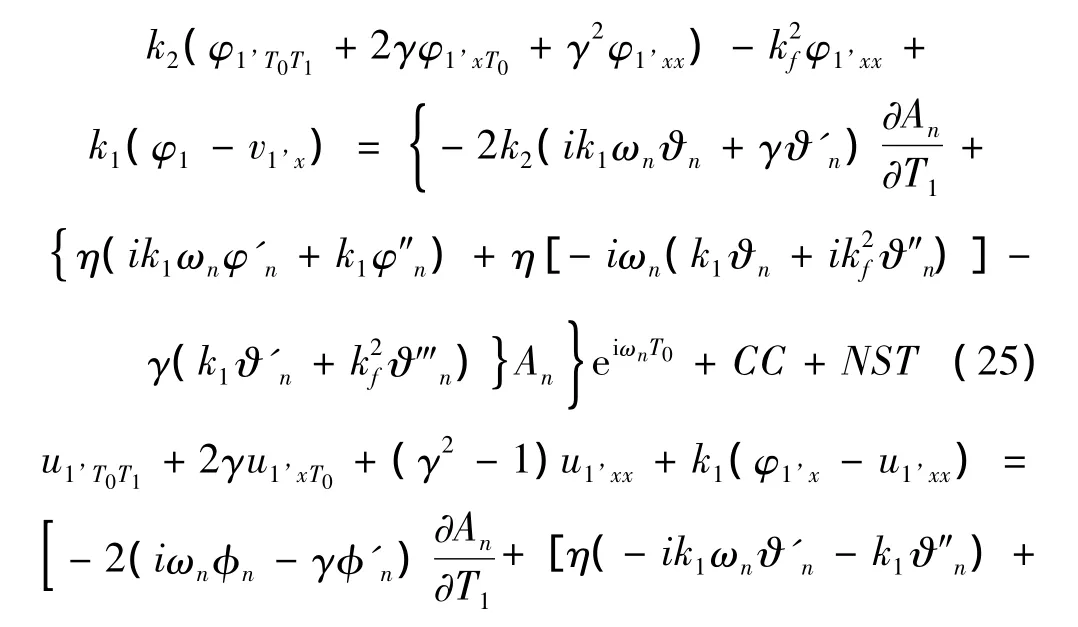
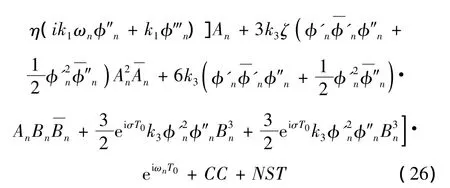
假设式(25)、式(26)的特解形式为:
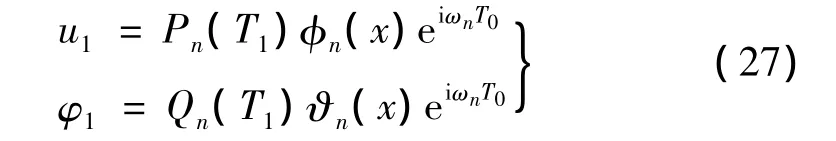
将式(27)代入式(25)、(26)令两端系数相等,得:
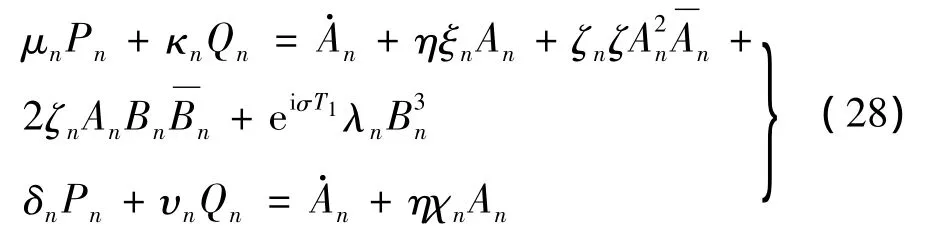
其中:
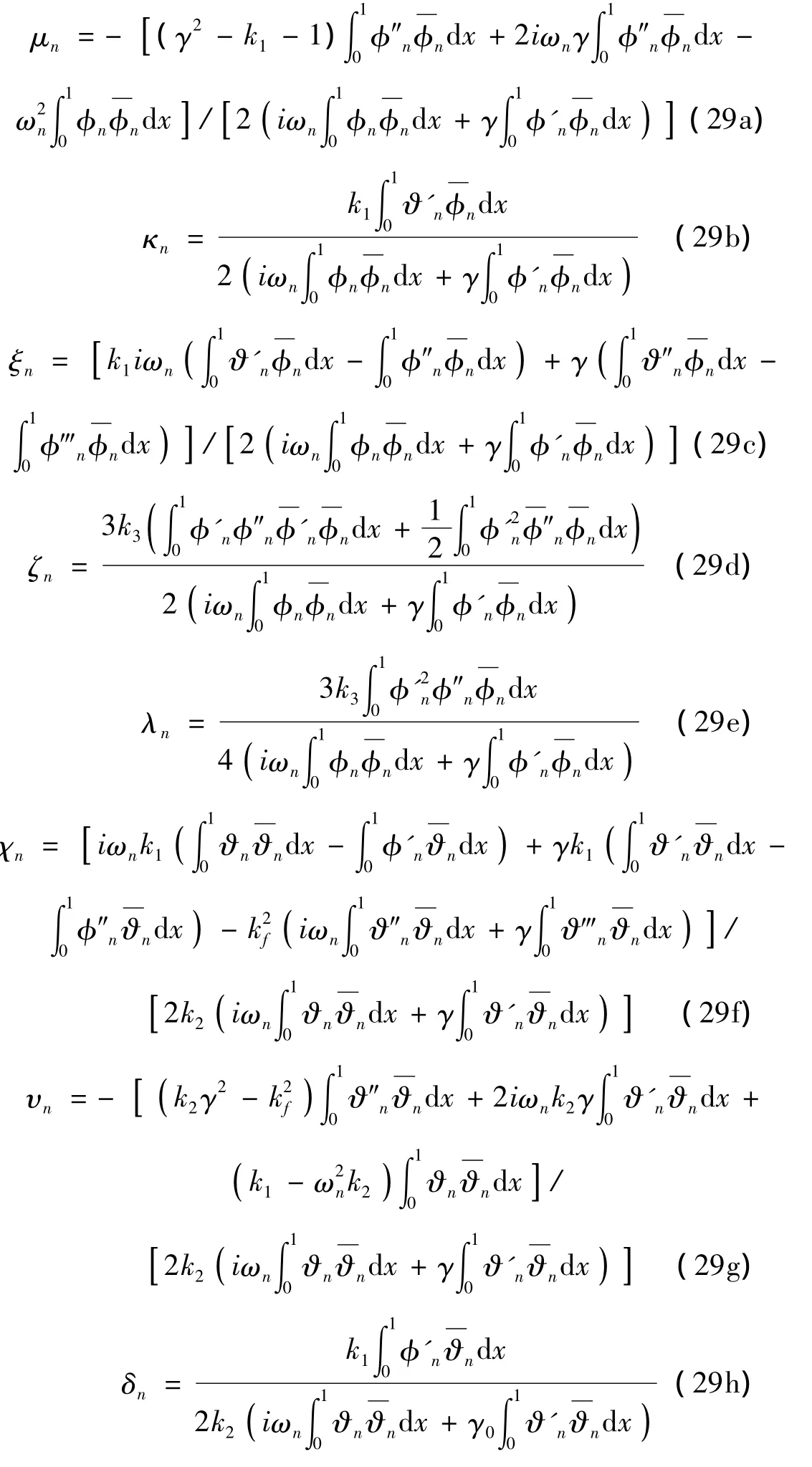
对系统所有参数,下式均成立:
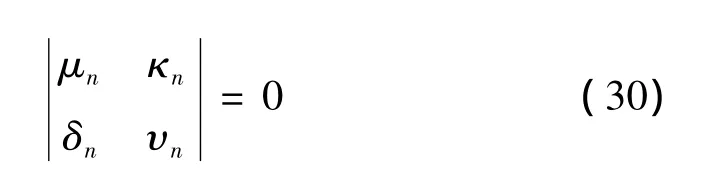
可解性条件可写成:
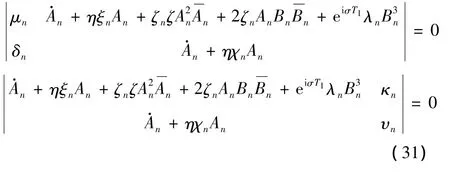
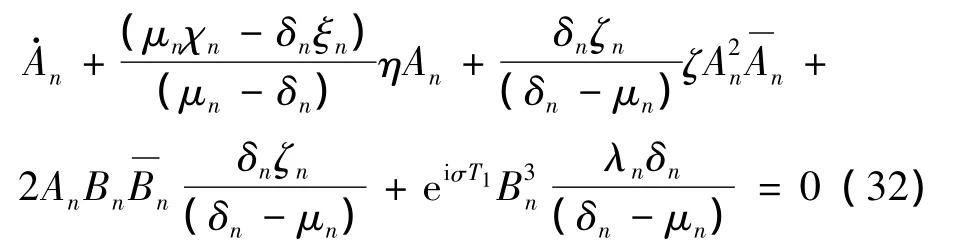
将式(32)写成极坐标形式:
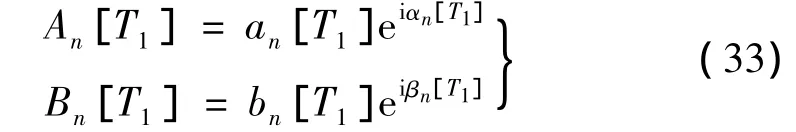
将式(33)代入式(32)并分离实部与虚部,导出:
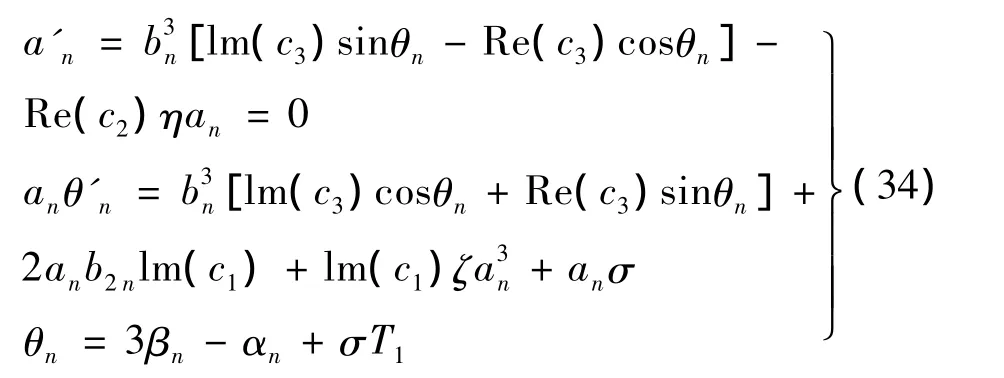
其中:
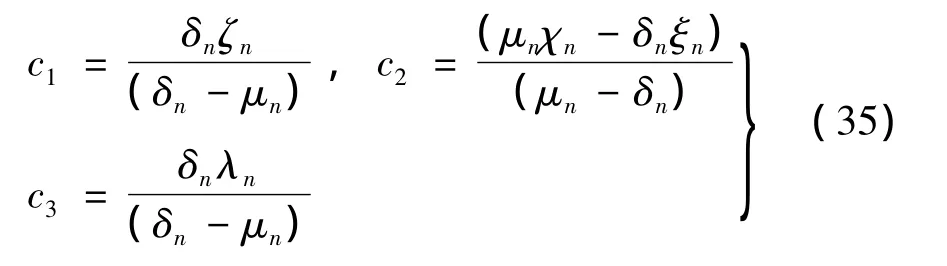
通过数值方法确定 μn,υn是正的纯虚数,κn,δn,ζn是负的纯虚数,ξn,χn为正的实数,λn为复数。c1为正实数,c2负纯虚数,c3为复数。如果存在稳态响应,幅值与相位必须满足:
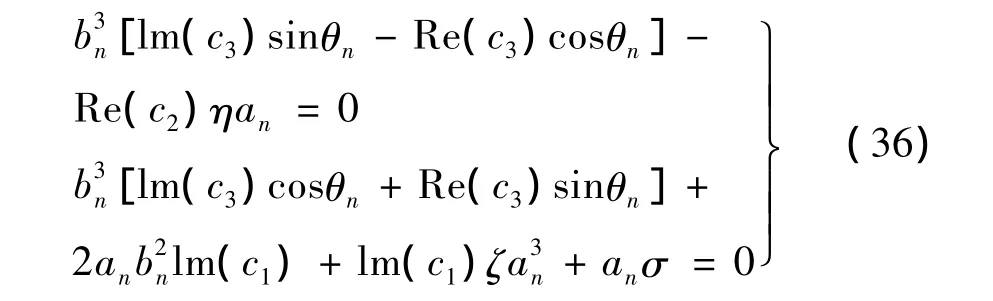
消去式(36)中相位,得第n阶模态共振的幅值响应与调谐参数关系:
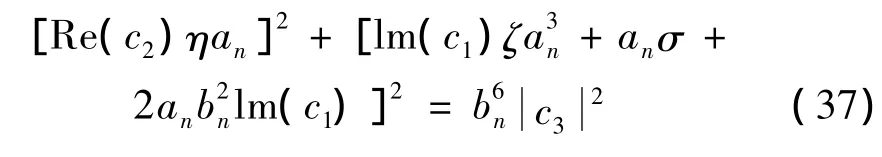
计算式(34)右端平衡解的Jacobi矩阵及特征方程,根据劳斯 -赫尔维茨判据,稳定条件及失稳边界为:
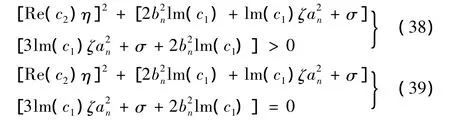
考虑轴向运动黏弹性Timoshenko梁参数为:截面积 A=9 ×10-3m2,轴向力 P=107N,长0.3 m,弹性模量 E=169×109Pa,剪切模量G=66×109Pa,截面系数κ =5/6。k1=71.28,k2=0.006 58,kf=0.8,γ =2。图2为外激力作用下第一、二阶幅频响应曲线。第一、二阶频率分别为:ω1=7.244,ω2=25.792。第一阶响应中参数为:b=0.005,η =0.001,ζ=5。第二阶响应中参数为:b=0.003,η =0.001,ζ=2。
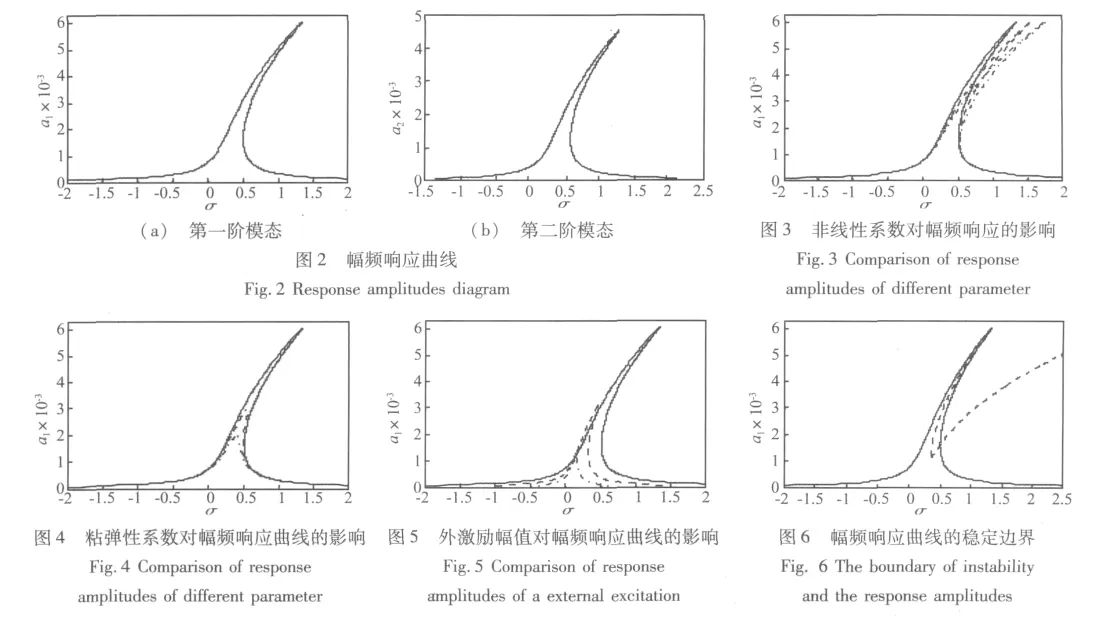
考虑轴向运动黏弹性Timoshenko梁参数为:k1=71.28,k2=0.006 58,kf=0.8,γ =2。图 3 为不同非线性系数对幅频响应曲线的影响。随着非线性系数的增大,响应曲线峰值向右弯曲。各个系数分别为:b=0.01,η =0.001。
图4为不同黏弹性系数对幅频响应曲线的影响。随着黏弹性系数的增大,响应振幅减小。各个系数分别为:b=0.01,ζ=5。梁参数为:k1=71.28,k2=0.006 5,kf=0.8,γ =2。图 5 为不同外力作用下对幅频响应曲线的影响。随着外力的增大,响应振幅增大。各个系数分别为:η =0.001,ζ=5。
图6为响应曲线以及失稳边界。实线表示响应曲线,虚线表示失稳边界,在该边界的区域不稳定,而外面稳定。在不稳定的区域内会出现跃跳现象。参数b=0.01,η =0.001,ζ=5。
3 结论
本文分析了轴向运动黏弹性Timoshenko梁的横向非线性强受迫共振的响应问题,梁的黏弹性用Kelvin本构关系并引入物质时间导数加以描述。运用广义哈密顿原理推导梁横向振动的控制方程以及边界条件。应用多尺度方法分析了系统超谐波共振时的稳态幅频响应,以及非线性、激励振幅和黏性阻尼对响应的影响。通过分析稳定点的线性化方程确定响应曲线的稳定性。数值结果表明,扰动振幅的增大使共振振幅增大,增大黏弹性阻尼使共振振幅减小,非线性系数增大使得共振振幅减小。
[1]冯志华,胡海岩.直线运动柔性梁非线性动力学—主参数共振与內共振联合激励[J].振动工程学报,2004,17(2):126-131.
[2]Chen S H,Huang J L,Sze K Y.Multidimensional lindstedtpoincare method for nonlinear vibration of axially moving beams[J].Journal of Sound and Vibration,2007,306:1-11.
[3]Marynowski K.Non-linear vibrations of an axially moving viscoelastic web with time-dependent tension [J].Chaos,Solitons& Fractals,2004,21:481-490.
[4]Mote C D J.Dynamic stability of an axially moving band[J].Journal of the Franklin Institute,1968,285:329-346.
[5]Simpson A.Transverse modes and frequencies of beams translating between fixed end supports[J].Journal of Mechanical Engineering Science,1973,15:159-164.
[6]杨晓东,陈立群.带有扭转弹簧两端铰支轴向运动梁的横向振动分析[J].振动与冲击,2006,25(4):149-150.
[7]丁 虎,陈立群.混杂边界条件下轴向变速运动黏弹性梁参数振动的稳定性[J].振动与冲击,2008,27(11):62-63.
[8]Ghayesh M H,Balar S.Non-linear parametric vibration and stability analysis for two dynamic models of axially moving Timoshenko beams[J].Applied Mathematical Modelling,2010,34:2850-2859.
[9]Lee U,Kim J,Oh H.Spectral analysis for the transverse vibration of an axially moving Timoshenko beam[J].Journal of Sound and Vibration,2004,271:685-703.
[10]Tang Y Q,Chen L Q,Yang X D.Nonlinear vibrations of axially moving Timoshenko beams under weak and strong external excitations[J].Journal of Sound and Vibration,2009,320:1078-1099.
[11]Tang Y Q,Chen L Q,Yang X D.Parametric resonance of axially moving Timoshenko beams with time-dependent speed[J].Nonlinear Dynamics,2009,58:715 -724.
[12]Chen L Q,Tang Y Q,Lim C W.Dynamic stability in parametricresonance ofaxially accelerating viscoelastic Timoshenko beams[J].Journal of Sound and Vibration,2010,329:547-565.

