结构动力方程求解中隐式格式向显式格式的转换

李常青，楼梦麟，蒋丽忠

(1.中南大学 土木工程学院建筑工程系，长沙 410000;2.同济大学 土木工程防灾国家重点实验室，上海 200092)

结构动力计算采用的逐步积分方法，有显式算法和隐式算法之分。隐式算法需要求解耦联方程组，当结构自由度数目很大(如上百万个)时，求解工作量非常大。而显式算法不需要求解方程组，且计算精度控制的要求比稳定性条件要求更高，因此显式算法的构造一直是研究的热点［1－6］。在关注隐式算法与显式算法区别的同时，隐式算法与显式算法之间是否有联系，隐式算法是否可转换为显式算法，转换以后算法的稳定性及精度会发生什么变化却很少有讨论。本文对此进行了深入的研究。

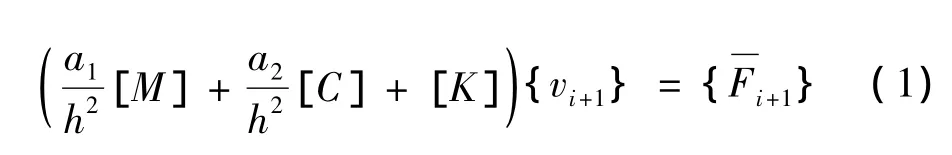
式中:［M］为质量矩阵，［C］为阻尼矩阵，［K］为刚度矩阵，{vi+1}为待求的位移向量，i+1}为广义的荷载向量，a1，a2为常数，对不同的加速度假设有不同的值。

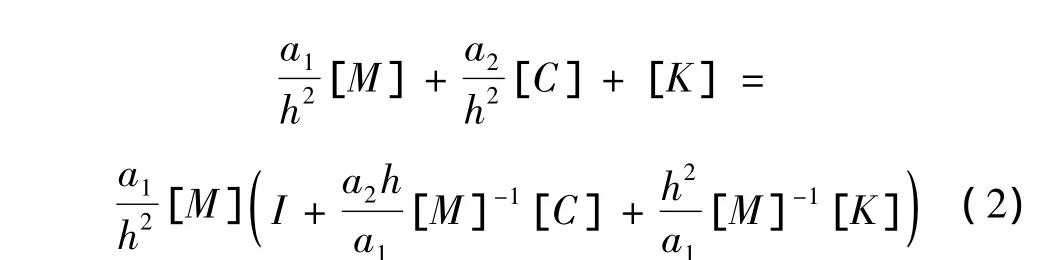
1 基本思路

广义线性加速度法是最常用的隐式算法之一，其中纽马克法与威尔逊－θ法均可看做广义线性加速度方法，每前进一步，都需要求解耦联线性方程组:

对式(2)矩阵求逆，得:

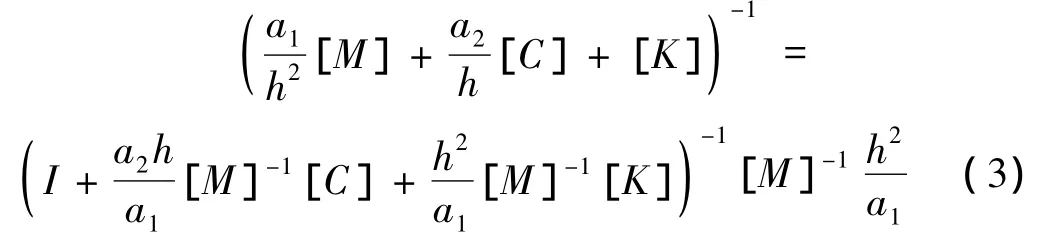
将式 (1)两 边 同乘 矩 阵

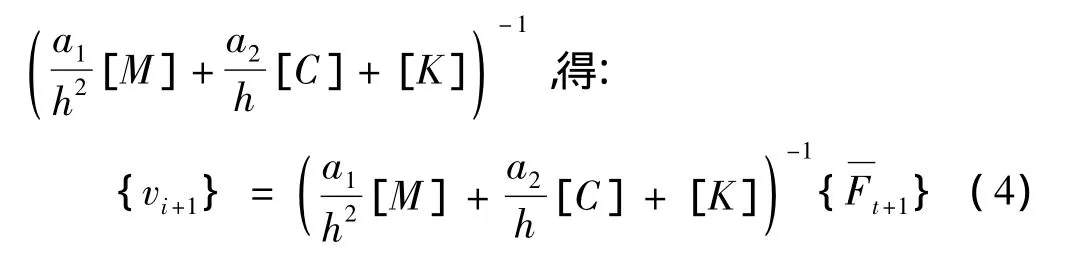
将式(3)代入式(4)，有:

级数展开式(5)中的逆矩阵，得:

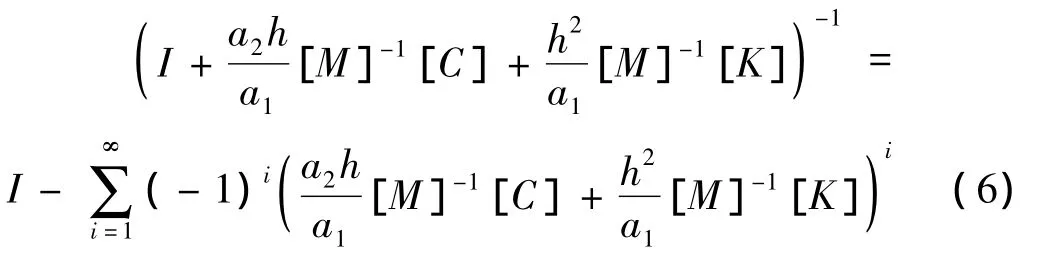
式(6)级数展开的收敛条件为摄动项范数不能大于1:

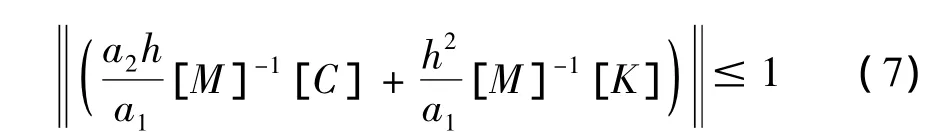
将式(6)代入式(5)，得无穷级数展开的显式算法:

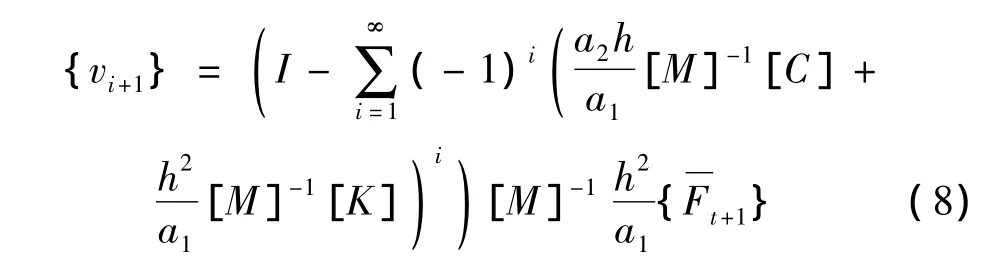
式(8)中的级数展开n次，即得级数截断后的近似公式:

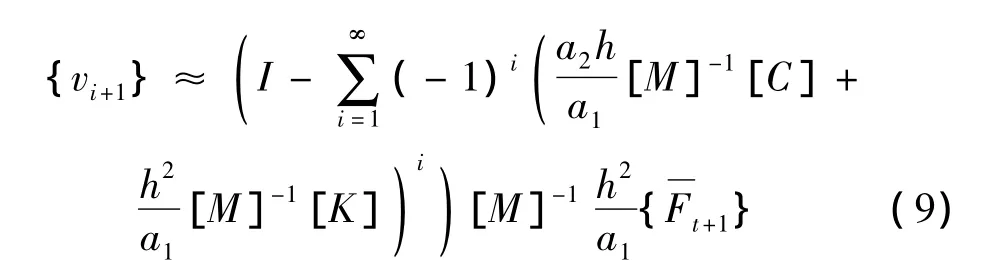
式(9)无需求解耦联线性方程组，避开了系数矩阵奇异时方程组无法求解的情况，因而提高了计算速度，节省了计算内存。

式(9)为对式(1)经求逆、级数展开、级数项截断后得到的近似，本文称式(9)为隐式算法(1)的伴随显式算法。下面分别详细分析无条件稳定的常加速度方法的显式化过程和条件稳定的线性加速度方法的显式化过程。

2 常加速度方法的显式化

2.1 公式推导

常加速度方法假定在两相邻时间之间，加速度为常数，其算法由下列三式构成:

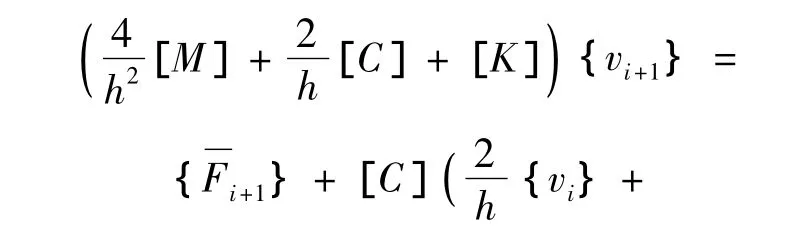
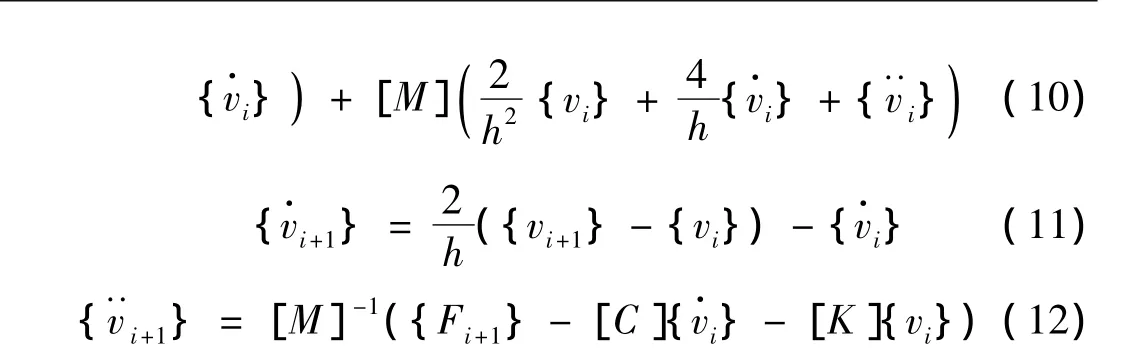
对照式(1)与式(10)可知，对常加速度方法，有a1=4，a2=2，因此通过前述的显式化过程，可得常加速度法的对应式(10)的显式化公式为:

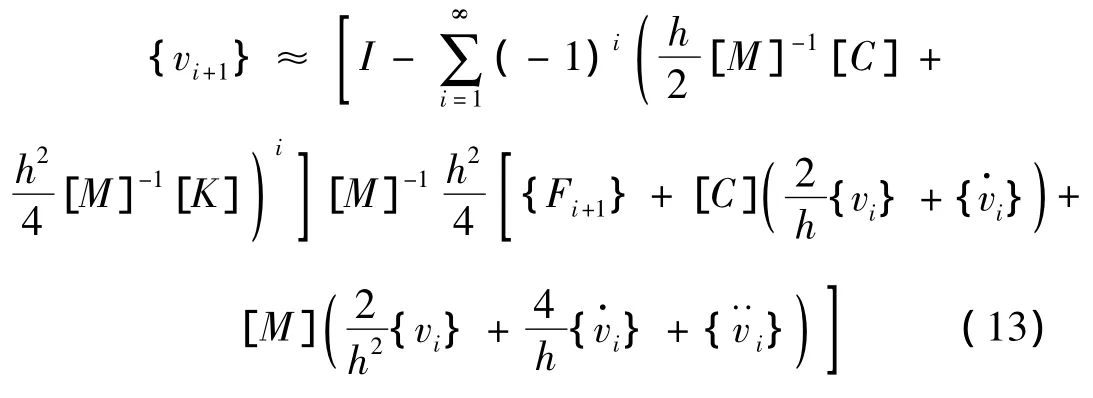
用式(13)求位移，式(10)求速度，式(11)求加速度，即得常加速度方法的伴随显式化算法。对应式(7)收敛条件为:

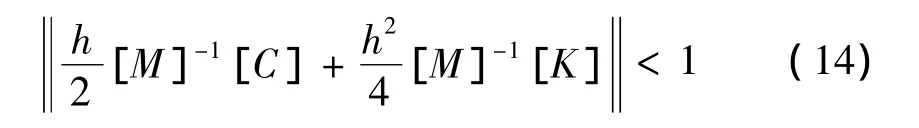
其中:

为任何一种矩阵范数。

考虑单自由度系统，式(14)化为

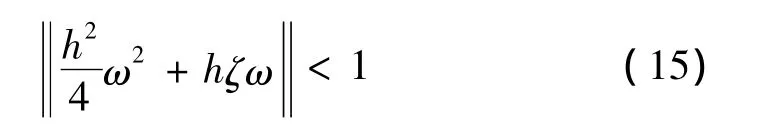
求解式(15)，得:

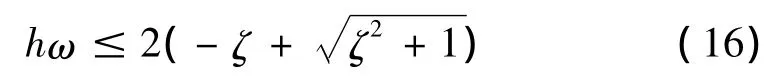
令 ζ=0，得:

化为h与T(结构周期)的形式为:

式(14)为级数展开的收敛条件，式(16)则是级数收敛条件在单自由度中的表现。下面的分析将表明，该逆矩阵级数展开的收敛条件对h/T的限制与按奇数项展开所得到算法的稳定性条件对 h/T的限制很接近。

导流装置的内外壁电解着色后均获得良好的黑色氧化膜，且肉眼看不出差异。于是采用CM-700d分光测色计分别测量了内外壁与仪器自带白色校准板之间的总色差(ΔE)。图3显示了内壁和外壁随机抽取的10个测量点的色差：内壁为91.25 ～ 92.06，平均值91.71；外壁为90.36 ～ 92.69，平均值91.41。内外壁的ΔE平均值仅相差0.3，说明内外氧化膜的颜色一致性良好。另外，内壁色差的离散度较外壁更低，说明内壁的颜色更加均匀。

2.2 精度分析

分析式(13)求解位移的精度。分别考虑n=1，2，3，4，5时的算法精度。位移计算误差定义为σv=ν理论－v计算，通过泰勒展开及符号运算，得到如下结果:

当k=1时，位移算法精度为二阶，位移误差项为:

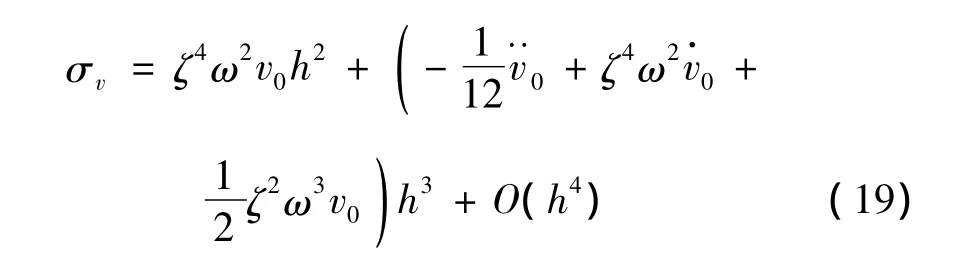
当k=2时，位移算法精度为三阶，位移误差项为:

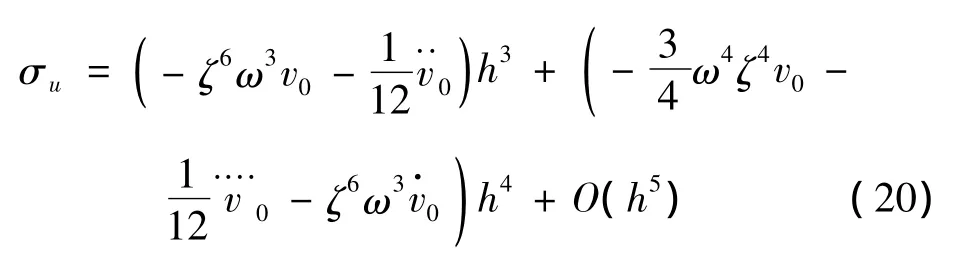
当k=3时，位移算法精度为三阶，位移误差项为:

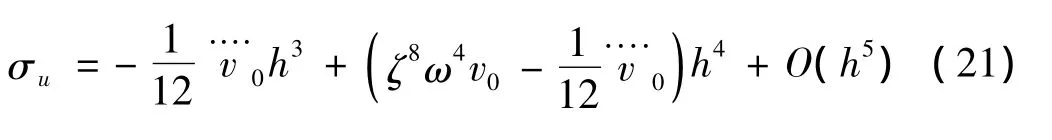
当k=4时，位移算法精度为三阶，位移误差项为:

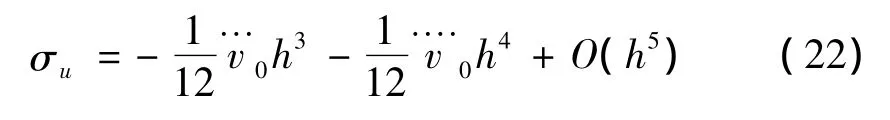
当k=5时，位移算法精度为三阶，位移误差项为:

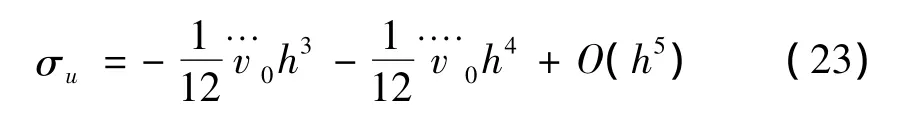
随着展开项数的增加，计算精度越来越高，但不会超过相应隐式算法的最高精度。当展开2项后，已达到了三阶精度。展开4项以后，计算精度增长不明显。当n=3、4、5时，位移算法精度为三阶，速度算法精度(式(11))为二阶，加速度算法精度亦为二阶，因此，本算法可达到二阶精度。建议采用n=3。

2.3 稳定性分析

算法的稳定分析，通过计算单自由度系统得到传递矩阵，形式如下:

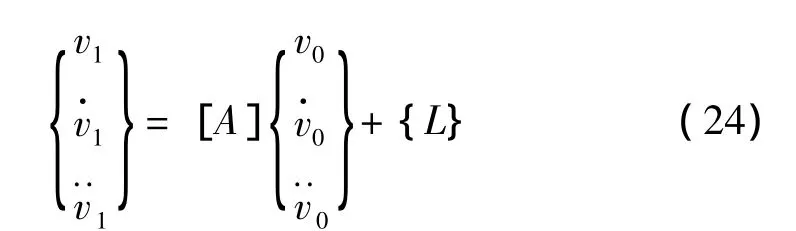
分别考虑n=1，2，3，4，5时算法稳定性的表现。由于传递矩阵［A］形式很复杂，尤其当5阶展开时，形式更复杂。此处只列n=1时算法的传递矩阵［A］，其各分量为:

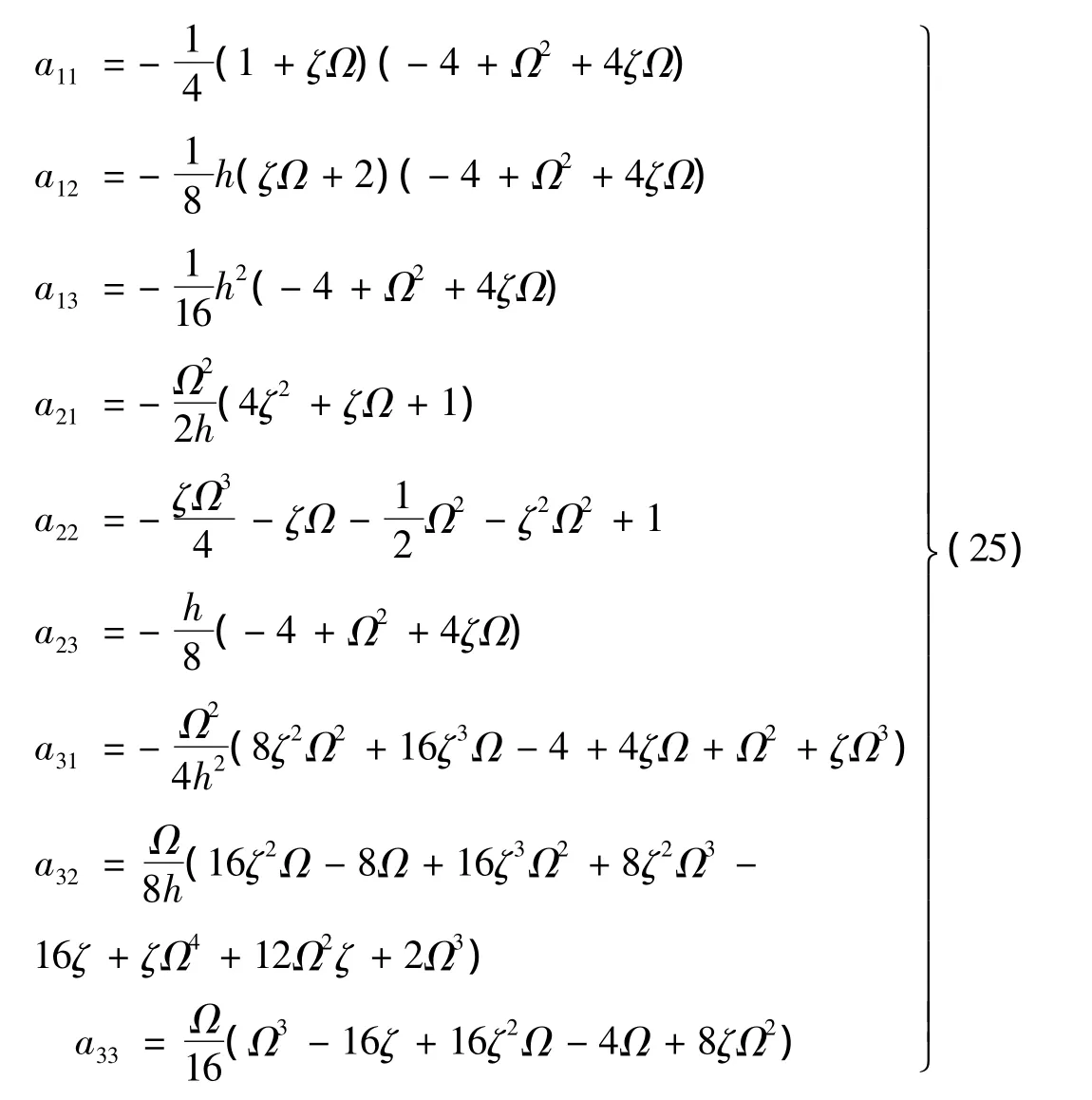
算法的稳定性要求:

其中:ρ(A)为矩阵A的谱半径。

图1为当n取不同值时，传递矩阵A的谱半径随h/T及阻尼比ξ的变化过程。

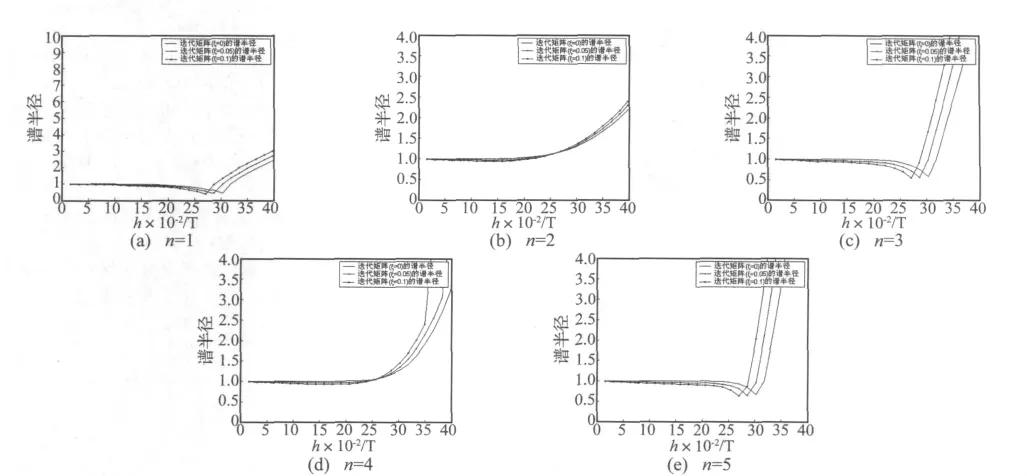
图1 常加速度法伴随显式算法传递矩阵A谱半径的变化Fig.1 Spectral radius of transferring matrix of constant acceleration method’s adjoint explicit method

表1 常加速度对应显式算法稳定域大小(h时间步长、T周期)Tab.1 Stability field of constant acceleration method’s adjoint explicit method

表2 常加速度伴随显式算法(n=3)稳定性和级数收敛性对h/T的限制的对比Tab.2 H/T’s limited field of constant acceleration method’s adjoint explicit method

表1列出了阻尼比分别为 0，0.05，0.1，而 k 分别为1，2，3，4，5时常加速度伴随显式算法的稳定区间。

表1显式:n为奇数时算法的稳定性明显优于n为偶数时算法的稳定性，建议采用奇数次级数展开。

h/T的取值受限于算法稳定条件，见表1，同时也受限于逆矩阵展开时的收敛性条件，见式(16)。表2详细列出了当n=3时显式算法的稳定域大小与级数收敛条件域大小的区别。表2显示，两个不同要求对h/T的限制非常接近。

3 结论

广义线性加速度法求解的耦联线性方程组，其系数矩阵由结构的刚度阵、质量阵/时间步长的平方、阻尼矩阵/时间步长的一次方等三项线性组合而成，随着时间步长趋于零，质量阵权重加大，而刚度阵与阻尼阵的权重减少。据此，本文构造了以质量阵项为主，刚度阵、阻尼阵组合相关项为摄动项，对系数矩阵的逆矩阵在单位阵附近进行级数展开的显式算法。详尽分析了常加速度法方法的显式化过程。公式推导中，逆矩阵级数展开的收敛条件与算法本身稳定性条件均被满足，两者对h/T提出的限制域很接近。级数展开奇数项算法的稳定性明显优于级数展开偶数项算法的稳定性。

分析结果表明，无条件稳定的常加速度隐式算法，通过求逆、级数展开的步骤后得到的显式算法，不再维持原隐式算法的无条件稳定性，即使级数展开很多项，也不能明显改善显式算法的稳定性能。对于常加速度法的伴随显式算法，逆矩阵的展开项达到3时，即可使显式算法达到相应隐式算法的精度。

本文给出了隐式算法和显式算法之间的联系，提供了一种构造显式算法的新思路:即可按高精度的隐式算法构造相应精度的显式算法。换言之，隐式算法精度有多高，对应的显式算法精度即能达到多高。本文这种多项式加速度显式算法的计算精度与精细积分方法［7－9］相差不多，而计算效率却高一个数量级。

［1］李小军，廖振鹏，杜修力.有阻尼体系动力问题的一种显式差分解法［J］.地震工程与工程振动，1992，12(4):74－79.

［2］李小军，廖振鹏.非线性结构动力方程求解的显式差分格式的特性分析［J］.工程力学，1993，10(3):141－146.

［3］杜修力，王进廷.阻尼弹性结构动力计算的显式差分法［J］.工程力学，2000，17(5):37－43.

［4］王进廷，杜修力.有阻尼体系动力分析的一种显式差分法［J］.工程力学，2002，19(3):109－112.

［5］张晓志，程 岩，谢礼立.结构动力反应分析的三阶显式方法［J］.地震工程与工程振动，2002，22(3):1－8.

［6］陈学良，金 星，陶夏新.求解加速度反应的显式积分格式研究［J］.地震工程与工程振动，2006，26(5):60－67.

［7］钟万勰.暂态历程的精细计算方法［J］.计算力学学报，1995，1:1 －6.

［8］谭述君，钟万勰.非齐次动力方程Duhamel项的精细积分［J］.力学学报，2007，3:374 －380.

［9］高小科，邓子辰，黄永安.基于三次样条插值的精细积分法［J］.振动与冲击，2007，26(9):75－82.