基于车体动态特性的发动机安装位置优化

张志飞，倪新帅，徐中明，余 烽

(1.重庆大学 机械传动国家重点实验室，重庆 400030;2.重庆大学 机械工程学院，重庆 400030)

全地形车由于行驶路况比较复杂，因而对其动态性能提出了很高的要求。全地形车车架挂发动机结构(简称为车体)动态特性的好坏，很大程度上决定其整车振动舒适性及可靠性。因此改善车体的动态特性是提高全地形车舒适性和安全性的关键。目前对于改善车体动态特性的研究主要集中在对车架结构的改进方面，如改变车架的板厚和管径［1－3］以及在车架薄弱位置添加加强板［4－5］等，很少考虑优化发动机安装位置及俯仰角度。

形状优化是结构优化领域中一个重要分支，工程中应用广泛。如发动机叶片形状、大型压力容器、机器支架及开孔板结构的形状、大型水坝形状等。文献［6－7］利用形状优化的方法对车身地板结构进行了优化，使车内噪声传递函数方均根值降低了2 dB，改善了车内噪声;文献［8］利用形状优化的方法对风力机叶片的弦长、扭角和相对厚度进行了优化;文献［9］发展了一种基于CFD技术的数值优化方法，对离心压缩机进气室几何形状进行了优化。

本文在对全地形车车体进行模态分析的基础上，利用形状优化方法对发动机在车架上的安装位置与俯仰角度进行优化，改善了车体的动态特性，为在设计阶段和改进阶段解决发动机在车架上的布局问题，提供了指导。

1 全地形车车体模态分析

1.1 车体计算模态分析

首先利用HyperMesh软件建立全地形车车体的有限元模型，然后运用MSC.Nastran软件进行计算模态分析。该车车架的主要结构为钢板、圆管，其厚度与长度和截面尺寸相比很小，故采用shell单元进行模拟，大小为6 mm。横梁与纵梁之间多为点焊，用一维单元RBE2模拟。在建模过程中作一些简化，忽略对车架模态影响很小的如座椅支承座、货架支承座及前后悬架支承座等附件。

在车架有限元模型的基础上，文献［10］的方法将发动机(含离合器、变速器、分动器)简化为一个质心、质量、转动惯量与该车发动机均相等的长方体，并网格化，通过SPRING单元将发动机与建立在车架上的MPC单元连接，模拟车架挂发动机状态。建立车架挂发动机总成的有限元模型如图1所示。

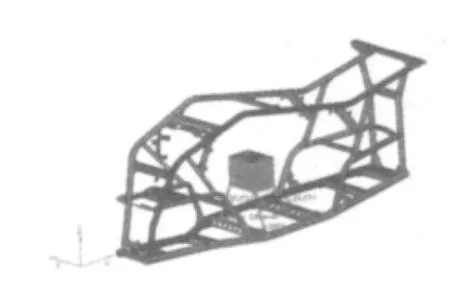
图1 全地形车车架挂发动机有限元模型Fig.1 Finite element model of ATV bodywork

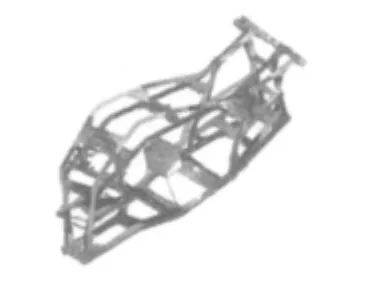
图2 全地形车车体的一阶模态振型图Fig.2 The first modal shape of ATV bodywork

对于全地形车而言，由于其车速不高，因此较关心车体的低阶模态。利用兰索士法提取车体前五阶自由模态，见表1，图2为车体的一阶模态振型。

由于在车体有限元建模过程中有许多假设与简化，因此模型的准确性需要通过模态试验检验。

1.2 车体试验模态分析

试验模态分析即通过对系统施加某种激励，测出响应，根据频率响应函数识别结构模态参数。试验模态分析可用于验证计算模态分析的准确性。

利用LMS模态测试系统进行试验模态分析。该车的车体采用钢管焊接结构，具有良好的线性特性，因此在进行模态试验时采用力锤激励。为模拟自由状态，将车体用软橡皮绳悬挂起来。根据车体的结构特点，通过多次预试验，最后选定的试验测点布置图如图3所示。

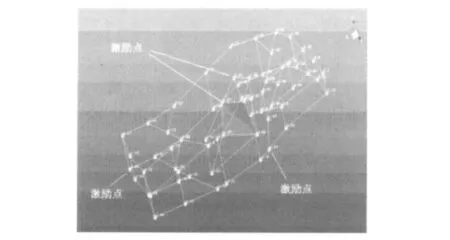
图3 全地形车车架挂发动机测点布置图Fig.3 The measured points of ATV bodywork

解析法和试验法的模态分析结果见表1，对比表明，二者频率接近而且振型一致，误差满足工程参考要求。同时也证明了车体建模准确，可以作为进一步优化设计的基础模型。

表1 全地形车车体前五阶模态分析结果Tab.1 The first five modes of ATV bodywork

1.3 车体动态性能分析

全地形车在行驶的过程中，激励来自路面不平度及发动机，应尽量避免激励频率与车体固有频率的耦合，从而提高乘坐的舒适性与车体的可靠性。

全地形车以车速v(km/h)行驶在不平度波长为λ(m)的路面时，时间频率f(Hz)为:

f=v/(3.6λ)

各种路面的不平度波长［11］如表2所示。

表2 不同路面的不平度波长(m)Tab.2 The irregularity wavelength of several road surfaces(m)

以该款全地形车的最高车速70 km/h为准，取路面不平度波长为最小值0.32 m，求得路面可能产生的最高激励频率为f=60.76 Hz，大幅低于车体的一阶固有频率76.9 Hz，所以路面不平度的激励不会引起车体共振。

作为整车的主要振源，发动机的振动很大程度上影响到车体的动态性能。该款全地形车采用单缸四冲程发动机，常用工作转速为:3 000 r/min～8 000 r/min。往复惯性力的基频为:f1=n/60;其中n为发动机转速。发动机一阶往复惯性力频率为:50 Hz～133 Hz。该款全地形车车体的一阶弯曲频率为154.0 Hz，理论上正常行驶时不会出现车体共振。但文献［5］的研究表明，摩托车发动机激励对车体侧弯与扭转振型也有较大影响。该车扭转振型频率为76.9 Hz，处于发动机激励的频率范围内，因此需要提高该阶模态频率，以改进原车动态特性。

2 发动机安装位置与安装角度优化

全地形车车体是整车的骨架，其振动特性影响整车的动态特性。由上述的分析可知，该款全地形车车体的一阶模态频率偏低。文献［12］的研究表明，发动机的安装方式对挂发动机的车体结构特性影响很大，故本文提出通过优化发动机的安装位置及俯仰角度改善车体的动态特性。

2.1 形状优化

形状优化是建立在最优化理论和有限元分析的基础上，根据给定的设计约束条件，求解满足约束要求的某种性能达到最佳构形的优化方法。形状优化所研究的问题可以分为四种:①在可行集合中寻找出最优形状;②找出给定形状的最好位置;③识别区域的边界，称为形状识别问题;④为自由边界问题。全地形车发动机安装位置和俯仰角度的优化所涉及的为第二类问题，故本文利用结构优化软件OptiStruct的形状优化功能来解决发动机的安装位置和俯仰角度的优化问题。

OptiStruct软件求解形状优化问题的基本方法是:首先在有限元模型上定义若干控制点和相应的域，通过改变控制点位置调整域的形状与空间位置，从而生成相应的扰动矢量Di用于定义与原始网格相关节点位置的改变。由此，结构的形状改变就可以被定义为扰动矢量的线性组合，即:

式中:X为节点坐标矢量，X0为节点初始的坐标矢量，Pi为设计变量，为扰动矢量Di对应的权重因子，一般取值在－1～1之间。

在优化迭代过程中，通过优化设计变量Pi值不断调整节点位置，使结构形状的发生改变，以得到最佳的结构形状。

2.2 建立优化模型

优化问题有三要素:优化目标、约束条件及设计变量。本文优化目标为车体一阶模态频率f1最大化。约束条件为:车体二～五阶模态频率(f2～f5)不小于原车频率。

在建立设计变量之前，首先用HyperMorph模块建立一个包含发动机所有单元的3D域及相应的8个控制点，通过这些控制点的位置改变生成四个扰动矢量Di，分别为:发动机相对于车架沿前后方向刚体平移50 mm的扰动矢量D1、沿左右方向刚体平移50 mm的扰动矢量D2、沿上下方向刚体平移50 mm的扰动矢量D3和绕车架横向旋转15°的扰动矢量D4。将四个扰动矢量Di对应的权重因子Pi定义为设计变量。发动机沿前后方向平移的扰动矢量D1如图4，各设计变量变化范围详见表3。

表3 设计变量Tab.3 Design variables

所建立的车体形状优化数学模型为:

图4 发动机沿前后方向平移的扰动矢量Fig.4 The disturbance vector of engine translating in anterior/posterior direction

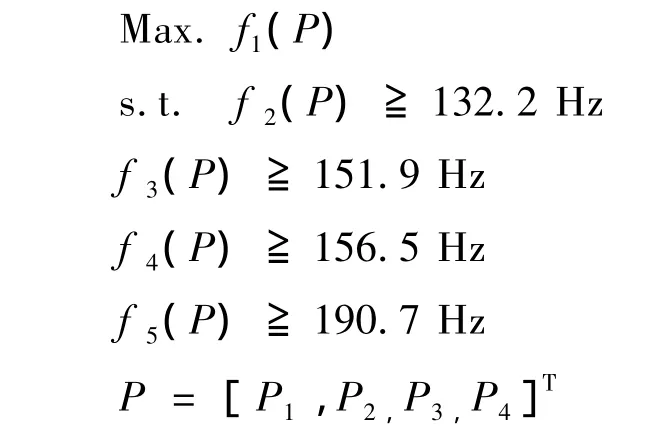
式中:P为设计变量，fi(P)为响应函数。

优化模型建立后，提交OptiStruct进行形状优化计算。

2.3 优化结果

响应量优化前后结果对比见表4:优化后车体一阶模态频率提高了4.9 Hz，其他四阶频率的变化较小，在一定程度上改善了车体的动态特性。

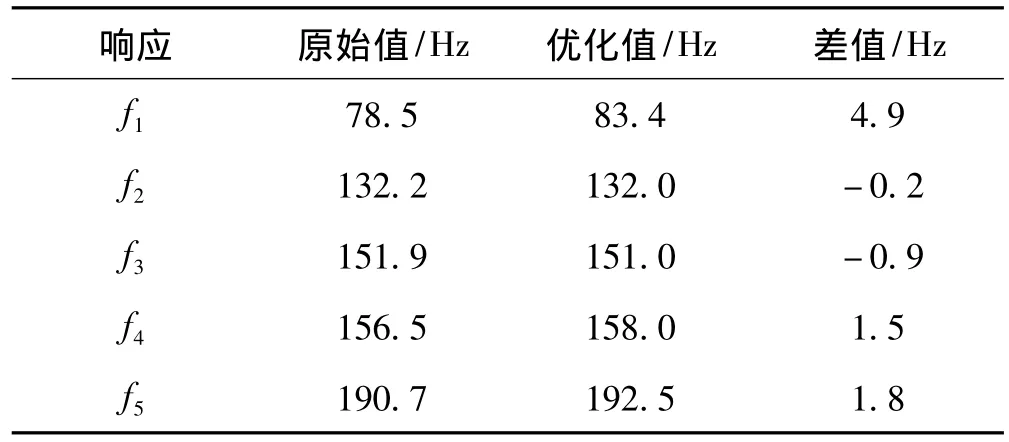
表4 响应量的优化结果Tab.4 The optimization results of responses

设计变量的优化结果见表5。优化后发动机在车架上安装位置和俯仰角度的改变为:向后平移17 mm，向右平移40 mm，向上平移1.5 mm，绕横向顺时针转动10.2°。优化后的车体模型如图5所示。

表5 设计变量的优化结果Tab.5 The optimization results of design variables

经过优化，车体的一阶模态频率有所提高，动态特性得以改善。由于受到改动范围的限制，优化效果不是非常明显。如果在设计阶段进行发动机安装位置及俯仰角度优化，效果会更好。

图5 优化后车体模型Fig.5 The optimized ATV bodywork

3 结论

为改善全地形车车体的动态特性，以有限元模型为基础，利用形状优化的方法对发动机在车架上的安装位置及俯仰角度进行了优化。结果表明:通过调整发动机的安装位置与俯仰角度可改善车体的动态特性;在发动机安装位置的设计与优化中，形状优化方法是可行与有效的;但优化的结果尚需试验的验证。

［1］张先刚，朱 平，韩 旭.摩托车车架的动态特性分析及减振优化研究［J］.中国机械工程，2005，16(12):1114－1117.

［2］颜长征，邓兆祥.以摩托车整车为基础的车架振动响应优化设计［J］.现代制造工程，2008(10):83－86.

［3］张志弘，何玉林，杜 静，等.摩托车整车振动性能匹配优化设计技术的研究［J］.中国机械工程，2005，16(23):2134－2137.

［4］徐中明，郭师峰，张志飞，等.全地形车车体动态特性分析［J］.重庆大学学报，2009，32(1):6 －10.

［5］徐中明，张志飞，周 坤，等.摩托车振动舒适性分析与改进［J］.中国机械工程，2007，18(24):3009－3013.

［6］Marburg S.A general concept for design modification of shell meshes in structural-acoustic optimization-PartⅠ:formulation of the concept［J］.Finite Elements in Analysis and Design，2002，38(8):725 －735.

［7］Marburg S.A general concept for design modification of shell meshes in structural-acoustic optimization-PartⅡ:application to a floor panel in sedan interior noise problems［J］.Finite Elements in Analysis and Design，2002，38(8):737 －754.

［8］陈 进，王旭东，沈文忠，等.风力机叶片的形状优化设计［J］.机械工程学报，2010，46(3):131 －134.

［9］陈宗华，谷传纲，舒信伟.基于CFD技术的离心压缩机径向进气室结构形状优化设计［J］.机械工程学报，2010，46(14):124－129.

［10］邱兆强.全地形车整车振动分析与优化［D］.重庆:重庆大学，2010.

［11］高国生，张祖翰.摩托车车架动态特性性能的试验研究［J］.振动与冲击，1994，13(3):66 －69.

［12］张志飞.摩托车及全地域车行驶动力学研究［D］.重庆:重庆大学，2008.