飞轮扰动作用下卫星结构响应能量预示方法

王 坤，赵 阳，马文来，王有懿

(哈尔滨工业大学 航天学院 航天工程系，哈尔滨 150001)

航天事业的不断发展对航天器的指向精度及稳定性提出了更高的要求，在轨运行期间的各种干扰降低了天线和相机等有效载荷的工作性能，飞轮作为最主要的干扰源之一，严重影响卫星等航天器的姿态控制精度和稳定性，成为制约我国高精度航天器发展的主要因素［1］。研究航天器在飞轮作用下的动态响应特性，是抖动抑制的基础，对我国研发高精度和高稳定度航天器具有重要意义。

研究飞轮扰动下航天器结构动态响应特性的方法主要是有限元法［2］，作为一种数值解法，为保证解的合理性，在划分有限单元时需保证每个波长之内包含一定数目的单元［3］，这样，网格密度和计算成本会随着结构振动频率的升高而增加，故实际工程中，有限元技术局限于低频振动分析领域。

为解决航天器结构中高频响应问题，田浩等［4］将波动方法用于卫星框式结构的抖动特性分析。波动法可对全频域进行确定性描述，但它在高频域对边界条件的数学模型要求较高，也具有一定局限性。

有限元法和波动方法的一个主要缺陷在于其以位移为变量，力求得到结构所有位移和所有频率的精确解，因而导致了响应预示结果对结构模型敏感和计算成本的增加。能量方法的出现在一定程度上解决了这一问题。Lyon［5－6］给出了基于能量方法的结构振动分析，这奠定了统计能量分析的基础。能量方法具有计算量小、且变量对边界条件不敏感等特点，因而在处理高频域结构振动响应问题中得到了很大发展。统计能量分析的基本要求是高模态密度，对模态密度较低的中低频域，要得到中低频响应的能量预示结果，就需要突破模态密度的限制。Nefske等［7］在研究梁的振动问题时，得到了类似热传导方程的能量方程，该方法结合有限元技术，发展为能量有限元法，与统计能量分析一样，用能量作为变量，计算量较小，可分析高频域的响应。能量有限元由于不涉及模态密度，适用的频域范围比统计能量分析更广，其结果可以精确到每个单元，且能得到更为精细的响应预示结果［8］，Cho［9］研究了典型耦合结构间的能量传递关系，使此方法更接近于实际工程应用。

在 Bouthier和 Cho基础上，Wang［10］发展了简化的能量有限元法，此方法在形式上与统计能量分析类似，可以方便的利用统计能量分析软件进行响应分析。Zhang［11］则针对船舶结构，分析了流体载荷下加筋板的能量密度响应。Yan［12］进一步地推导了复合材料结构的能量密度控制方程，为能量有限元法应用于复合材料结构提供了理论依据。Lee［13］结合周期理论，将能量有限元法推广到旋转体结构的计算，并与试验数据进行了对比验证。

鉴于能量有限元法的优势，本文将其引入航天器结构的振动响应分析。首先分析飞轮扰动模型的特性，而后基于能量密度控制方程，结合有限元技术对卫星框式结构进行抖动响应分析，为进一步研究抖动抑制提供理论依据。

1 飞轮扰动模型

文献［1］认为转子不平衡、飞轮结构挠性、轴承振动与摩擦以及电机的输出转矩等四方面是飞轮扰动主因。其中，转子不平衡是最主要因素，它由飞轮转子质量分布不均造成，可分为静、动不平衡两类，分别指飞轮转子质心与惯性轴不重合、飞轮转子惯性轴与旋转轴不重合而产生的扰动。当飞轮高速旋转时，这两种扰动将作为高频激励作用于航天器结构，使其产生高频响应，从而影响航天器的指向精度与稳定度。

根据作者前期研究［14］，通过对国内外文献分析综述，飞轮实验扰动模型为:

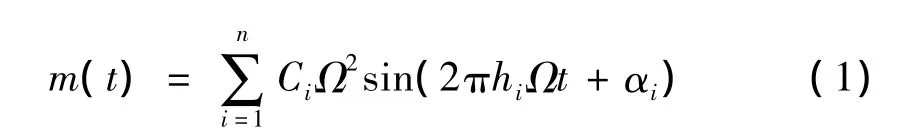
其中:m(t)为飞轮产生的扰动力或力矩(单位:N或Nm);n为模型中包含的谐波数;Ci为第i次谐波幅值(单位:N/Hz2);Ω为飞轮的转速(单位:Hz);hi为第i次谐波数;αi为随机相角，假定均匀分布在［0，2π］内。

由此可见，扰动模型中的扰动力或力矩可分解成飞轮转速的正弦波形式。其中谐波幅值Ci和谐波数hi需要利用振幅谱法和能量补偿法对实验数据进行参数辨识获取。本文作为理论方法研究，根据飞轮扰动可以分解为正弦波激励求和的特性，以单位正弦力作为激励，研究频域内结构的响应特性。在混响状态下，飞轮扰动产生的能量密度响应遵循线性叠加原理，飞轮扰动的响应以谐波幅值和谐波数作为对应频率响应的加权值求和即可得到。

2 能量密度控制方程

针对一控制体，根据能量平衡原理有:

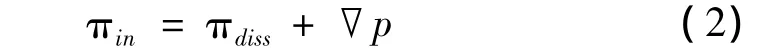
其中:p为控制体内做功功率;πin为外界输入功率;πdiss为损耗功率。

板的动力学方程为:

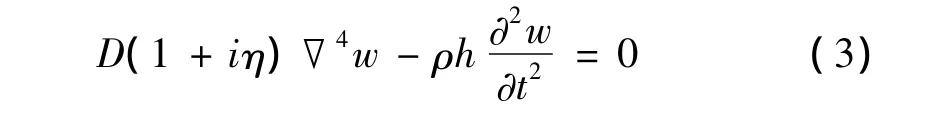
式中:D为板弯曲刚度，η为阻尼系数，w为板横向位移，ρ为板密度，h为板厚度，t表示时间。Bouthier［8］将板的横向位移表示为:

则方程可以写为:

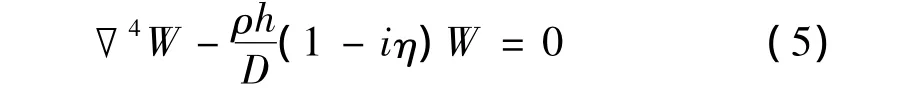
结构振动的解分为近场解和远场解，近场解只在不连续处附近起作用，在远离不连续处的位置，近场解很快衰减，只剩下远场解的作用，在结构振动响应全局分析时，近场解可以忽略，并且考虑到阻尼系数η是个小量，方程的解可以写为:

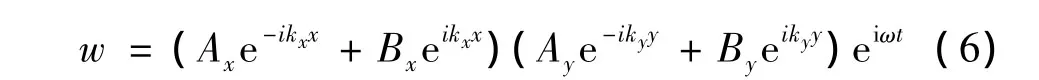
式中:kx，ky分别表示 x，y方向的波数。时间与空间平均能量密度为:

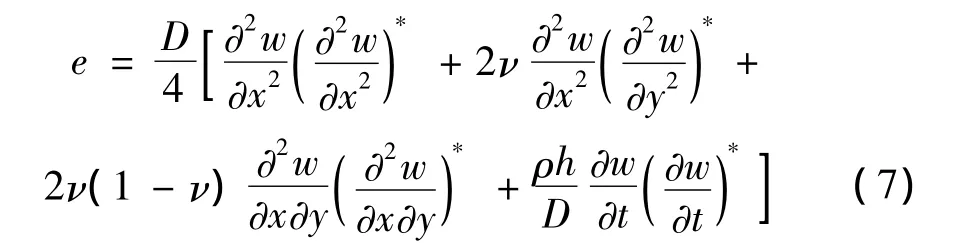
式中*表示求共轭。

功率为:

其中:

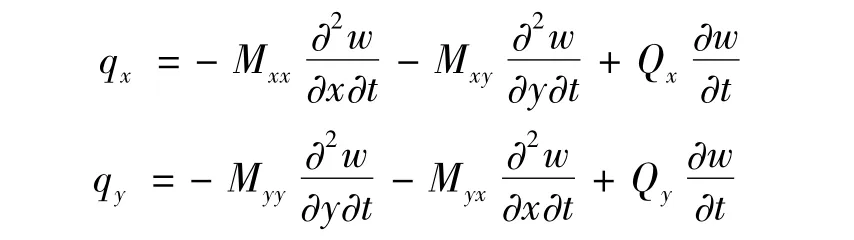
式中:Mxx，Mxy，Myx，Myy分别表示各方向弯矩，Qx，Qy表示各方向剪力。

将位移表达式代入，可得关系式:

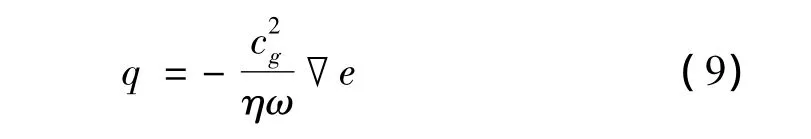
代入能量平衡方程可得板的弯曲波能量密度控制方程:

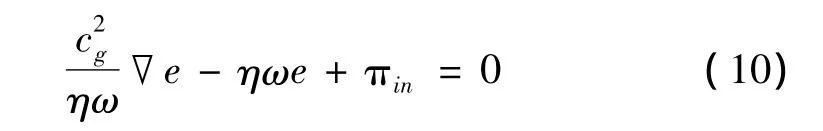
其中:ω为角频率;cg为弯曲波的群速度;e为能量密度。

由有限元理论［15］，根据加权余值法，其离散形

式为:

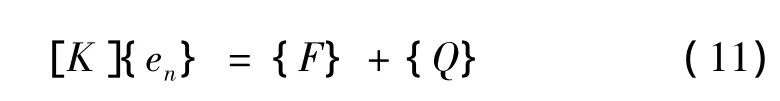
式中:

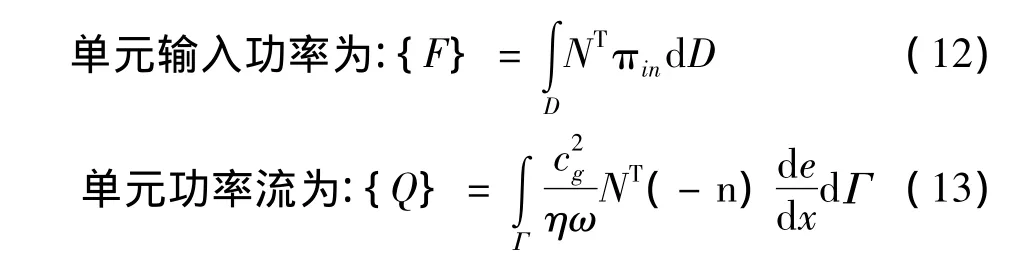
式中:Γ为单元边界;n为单元边界的单位方向矢量。NT为列向量，表示形函数向量的转置向量。

工程中的绝大部分结构都非单独的简单结构，而是由简单结构组合而成，因此需要进一步考虑简单结构间互相耦合的情况。

由于结构不连续处的能量密度不连续，耦合结构间的能量传递需要通过耦合处的功率流表示。对于二维连接节点为:

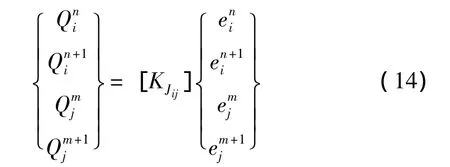
式中:Q为节点功率流，e表示节点能量密度值。下标i，j表示连接单元编号，上标 m，m+1，n，n+1表示对应连接单元的节点数。KJ称为连接矩阵，单元离散形式为:

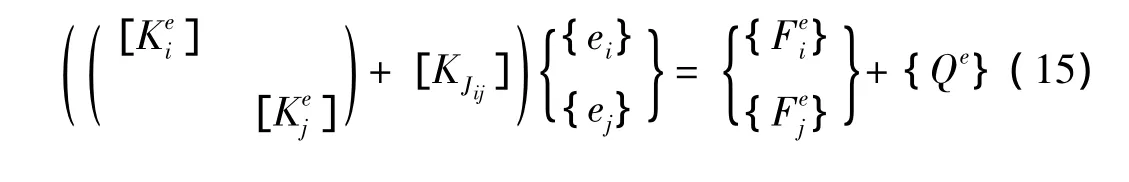
得到考虑耦合情况的能量密度控制方程整体有限元形式为:

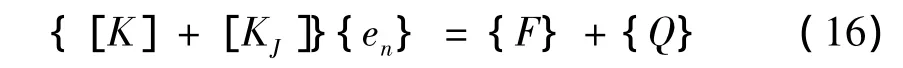
结构不连续处能量关系通过连接矩阵［KJ］实现。

3 算例及分析

本文设计的卫星框式承力结构如图1所示，板的几何尺寸均为1 m×1 m，模拟飞轮扰动的激励作用于板1中部位置，各板的密度为ρ=2 700 kg/m3，阻尼系数 η =0.001，泊松比 ν=0.3，弹性模量 E=7.1 ×1010N/m2，板厚 h=0.001 m。

卫星框式承力结构的每个面划分为24×24的四边形有限元网格进行计算。

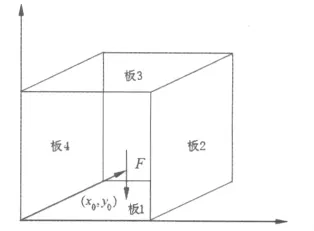
图1 卫星框式结构图Fig.1 satellite structure

板1是飞轮激励直接作用的板，当载荷频率为50 Hz、500 Hz 和 900 Hz时，对板1、板2的能量密度响应空间分布进行计算。

图2中，板 1的中部能量密度出现峰值，此处为激励作用位置，飞轮的扰动作为一种能量形式直接输入到此位置，因此该位置的振动幅度最大，即对应的能量值也最高。在其它位置，由于阻尼的存在，能量密度值逐渐减小，由于能量密度为空间域内的平均值，所以整体呈现平滑的分布状态。图3所示的板2由于没有激励源输入，整体呈现平滑状态，并且随着远离激励源，能量密度值逐渐降低。

由图2和图3所示各频率下板1和板2的能量密度响应对比可以看出，在板的连接处存在能量密度值的不连续，这是由结构耦合引起的能量密度损失导致，Cho对耦合结构间能量传递关系进行了深入研究，用能量的透射和反射系数表征结构耦合间的能量关系，并给出了典型耦合时能量反射系数和透射系数的解析表达式［9］，但在工程中并不适用，实际中，耦合结构间的能量传递关系通常由实验得到，本文利用有限元程序通过分析结构的位移响应得到。

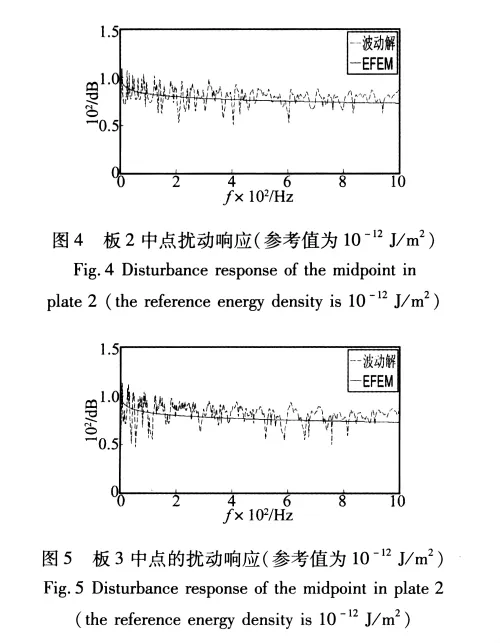
在频率域内，用能量有限元方法与传统波动方法得到的结果如图4和图5所示。经计算，板2中点的波动解平均值为79.6 dB，EFEM 平均值为77.3 dB;板3中点波动解平均值为81.5 dB，EFEM平均值为77.2 dB;平均值相差5%左右，并且能量有限元得到的值小于波动解的值，这种现象正是能量有限元法忽略近场解的体现。由图4和图5可见，近场解在低频范围内对结构振动的响应影响较大。以图4为例，低于200 Hz时，波动解的上下波动幅度较大，随着频率的升高，波长变短，近场解作用的范围随之变小，对整体结构的动态响应的影响也逐渐弱化，波动解在能量有限元解附近波动的幅度逐渐减小。

由图4和图5显示，传统波动方法得到的能量密度响应值呈现出密集的模态，对频率的变化敏感度很高，频率的微小改变会引起振动预示结果急剧变化，而利用能量有限元技术得到的响应曲线呈平滑变化状态，它预示的是在频域范围内平均的振动能量状态。

4 结论

本文基于飞轮扰动模型特性，针对卫星框式结构，采用能量有限元方法进行了结构响应预示研究，得出了以下结论与启示:

(1)飞轮扰动力在飞轮作用处的响应最大，响应值会随着与激励源距离的增大而减小，所以针对飞轮扰动的隔振在飞轮附近可以取得最好效果。

(2)能量有限元法预示的是卫星结构响应的平均效果，并且低于传统方法的预示值，相对于传统以位移为变量的方法，更适合中高频响应预示。

(3)能量有限元法在预示飞轮扰动时对频率变化不敏感。而实际工程中并不存在激励的精确模型，因此，能量有限元法的预示效果更具有参考价值。

飞轮是引起航天器扰动的主要因素但不是唯一因素，而且航天器的结构十分复杂，为更好的解决航天器扰动引起的指向精度等问题，需要综合考虑各种扰动的特征并结合更为精细的航天器模型进一步分析。

［1］王全武，虎 刚.飞轮扰动原因与测量技术现状［J］.空间科学学报，2009，29(1):39 －44.

［2］白争锋，赵 阳，马文来，等.反作用轮扰动对航天器结构动态特性的影响分析［J］.宇航学报，2009，30(5):2073－2079.

［3］韩增尧.有限元频响分析中网格划分技术研究［J］.强度与环境，2003，30(3):18 －22.

［4］田 浩，王有懿，刘春川.卫星框式结构扰动动态特性分析的行波方法［J］.哈尔滨工业大学学报，2010，42(5):696－699.

［5］Lyon R H，Maidanik G.Power flow between linearly coupled oscillators［J］.J Acoust.Soc.Am.，1962，34(5):623－639.

［6］Lyon R H，Scharton T D.Vibrational energy transmission in a three element structure［J］.J Sound and Vibration，1965，38:253－261.

［7］Nefske D J，Sung S H.Power flow finite element analysis of dynamic system:basic theory and application to beams［J］.Transactions of the ASME，1989，111(1):94－100.

［8］Bouthier O M，Bernhard R J.Simple models of the energetics of transversely vibrating plates［J］.J Sound and vibration，1995，182(1):149－164.

［9］Cho P E.Energy flow analysis of coupled structures［D］.West Lafayette:Purdue University，1992.

［10］Wang S.High frequency energy flow analysis methods:numerical implement-tation， applications， and verification［D］.West Lafayette:Purdue University，2000.

［11］Zhang W G.Energy finite element method for vibration analysisofstiffened platesunderfluid loading［D］.Michigan:University of Michigan，2003.

［12］Yan X Y.Energy finite element analysis development for high frequency vibration analysis of composite structures［D］.Michigan:University of Michigan，2008.

［13］Lee S M.Energy finite element method for high frequency vibration analysis of composite rotorcraft structure［D］.Michigan:University of Michigan，2003.

［14］孙 杰，赵 阳，田 浩.改善航天器反作用轮扰动实验模型参数识别方法［J］.空间科学学报，2006，26(1):70－74.

［15］Zienkiewicz O C.The finite element method［M］.New York:McGraw-Hill，1977.