拓展步行荷载对楼板振动响应影响的对比研究
陈 隽,叶 艇,彭怡欣
(1.同济大学 土木工程防灾国家重点实验室,上海 200092;2.同济大学 建筑工程系 安徽省建筑设计研究院有限责任公司,上海 200092)
近年来,随着材料性能、设计方法和施工手段的进步,特别是为了满足使用者对大空间的需求,大跨度楼盖结构日趋流行。由于大跨度楼盖柔性大、基频低、阻尼小(开放式楼盖),在使用者的步行等日常活动下可能产生振动,严重时会造成人体不适,导致振动舒适度问题。为此,国外很多规范都提出了楼盖振动舒适度的设计要求[1],我国混凝土结构新规范(GB50010-2010)也增加了对混凝土楼盖舒适度的设计要求。
楼盖振动舒适度控制一般通过限定竖向振动频率最小值或限定步行荷载作用下的最大振动幅值来实现。响应计算中步行荷载的动力特性是关键,然而“步行荷载曲线的研究目前国内尚较少,特别是对于针对中国人步行特点的测试和统计几乎没有”[2],实际设计中一般选取国外的步行荷载模型[2-4]。为此,作者开展了步行荷载曲线的实验测试工作[5-6]。由于实验中往往只能记录到单步荷载时程,需进一步拓展成连续完整的步行荷载曲线以研究步行荷载的动力特性,特别是频域特性。研究者基于不同的假定,先后提出了各种不同的步行荷载拓展方法。结合实验数据,本文通过分析比较混凝土方板在各拓展时程作用下加速度响应,讨论了各拓展方法的优劣,并建议了较好的拓展方法及其对应的实验测试要求。
1 步行荷载拓展方法
1.1 步行特点与步态周期
使用者在步行过程中对支撑结构所施加的力作用称为步行荷载,是一种动力荷载,在实验中一般采用固定于地面的测力板进行测量。一般地,运动生物力学将人行走过程的一个步态周期分为支撑阶段(支撑相)与摆动阶段(摆动相),一足完成一个支撑与摆动阶段称为一复步(即同一足足跟落地至下一次足跟着地的过程),双足同时落地的阶段则称为双支撑阶段[7]。双支撑阶段又可再划分为两个部分:一部分为初期双支撑阶段,即体重从对侧转移到本侧的阶段;另一部分为终期双支撑阶段,即体重从本侧转移到对侧的阶段。
由于步行荷载具有典型的时空变化的特征,受制于有限测力板数量,现有的人行荷载测试主要是测试单步(或一个复步)的步行荷载时程,需要利用一个单步(或复步)步行荷载时程拓展为完整的人行荷载时程,以进行后续的分析。拓展时一般假定步行时左右脚产生完全相同且重复的荷载曲线,而对双支撑阶段的不同假定导致了不同的拓展方法,主要有四种。
1.2 方法1——按步行时间拓展
步行时间为完成一个复步的时间,即同一足的足跟相邻两次接触地面的时间间隔。若测试中测得步行时间T,并假定左右两脚产生完全相同且重复的竖向荷载时程,一足从零时刻开始接触地面,对侧足在T/2时刻接触地面。那么,将单步落足时程曲线相继在时间轴上平移T/2后叠加,可得到连续的人行荷载时程[8]。
1.3 方法2——根据步行频率拓展
与方法1类似,若已知步行频率(即每秒步数)fs,则可将1/fs确定为重复周期 rp,单步落足时程曲线的时长t与rp的时间差(t-rp),即双足同时落地的持续时长。类似地,将单步落足荷载时程在时间轴上逐次平移rp后叠加,可得到连续步行荷载激励时程[9]。
1.4 方法3——按双支撑阶段时长拓展
若双足同时落地时间估计为0.1 s,实验中测得的单步落足荷载时程持续时间为t(单位为s),那么将单步时程在时间轴上逐次平移(t-0.1)s,并叠加,则可将单步落步时程拓展成连续步行荷载时程[10]。
1.5 方法4——按双支撑阶段时长比例拓展
正常对称步行中,双支撑阶段持续时间约占一个步态周期持续时间的20%,双支撑阶段又分为初期双支撑阶段与终期双支撑阶段,分别约占10%[11],而支撑相约占60%,可由此算出双足同时落地时间与单步落足时程持续时间之比约为1/6。那么,将单步落足荷载时程逐次平移其持时的5/6,并叠加,可将单步落足时程拓展为连续人行荷载时程。
2 基准荷载时程与响应计算方法
2.1 基准荷载时程
本研究采用三维动态捕捉技术(3D motion capture)与测力板相结合的方法开展步行荷载动力特性实验[5-6],系统构成原理及实际实验场地见图1。
每位测试者主要关键处安装有39个反光标记点(Marker),用于记录行走过程中人体关键点的运动轨迹。同时利用两块高精度测力板记录三向(竖向,水平前进和水平横向)的落步荷载曲线。
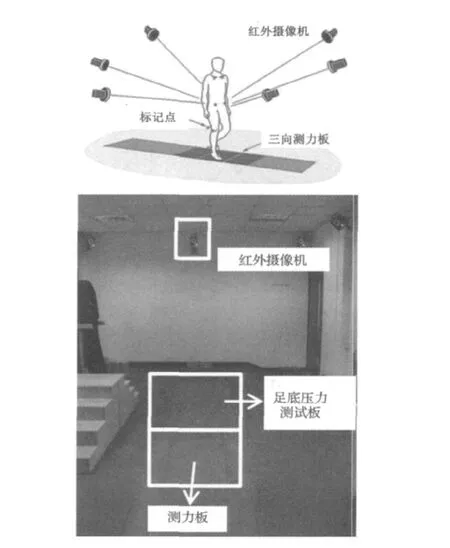
图1 步行荷载三维实验示意图Fig.1 Sketch map of 3D walking load experiment
根据Marker点的记录可以准确得到测试者走过测力板时一个完整复步内各支撑阶段以及下一个复步的开始时间。由此重复平移一个完成复步内的测力板数据可得到基准时程荷载曲线。由于基准时程采用一个复步时程扩展,且其计算参数完全由实验得到,因此基准时程是合理的。
2.2 步行荷载响应计算
通过对比不同扩展方法的时程与基准时程所引起的楼板响应来评价不同方法的优劣。选取一四边简支混凝土板为计算对象.板尺寸为12 m×12 m×0.305 m,混凝土容重取2 500 kg/m3,弹性模量取30 GPa,阻尼取0.05,板的基频经计算为6.8 Hz。采用宋志刚等[9]提出的基于振型分解的方法计算步行荷载作用下的矩形薄板响应。为说明该方法的适用性,用ABAQUS计算基准时程作用下方混凝土板的加速度,与上述基于振型分解方法对应结果对比。有限元模型中,混凝土板采用壳单元(S4R),采用瑞利阻尼,阻尼系数α、β由ξi=α/(2ωi)+βωi/2计算,取各阶阻尼比为0.05,前两阶频率为6.8、34.0 Hz,可得 α =3.560 5,β=3.900 9e-4。选用显式动态分析步(基于中心差分法)计算,网格大小为0.25 m×0.25 m,计算时步幅取0.75 m,只考虑板的第一阶振型。图2为两方法算得的板中心点处的加速度时程,其均方根值分别为:0.462 cm/s2(振型分解方法),0.468 cm/s2(ABAQUS),说明基于振型分解的响应计算方法合理。

图2 两种方法计算的基准时程加速度时程(实线:ABAQUS,虚线:振型分解)Fig.2 Acceleration time-history of standard trace calculated by two methods(solid line:ABAQUS,dashed line:mode decomposition)
3 计算结果与分析
基于三维动作捕捉系统目前已经完成60余人的荷载实验。从中取4位(2男2女)测试者在不同步频(慢、正常、快速自由行走;以及有节拍器引导的1.5,1.75,2.0,2.25 Hz四种固定步频)下三向共1 188 组拓展时程的对比分析。
3.1 拓展时程时频域对比
图3所示为一女性测试者(体重61 kg)固定步频1.5 Hz行走时拓展时程与基准时程的对比。实验中测试者根据节拍器的声音提示进行固定倍频行走。然而实验表明对于低步频(如1.5 Hz),测试者的实际步频很难保证与节拍器频率一致。由三维步态分析系统通过Marker点的位移变化确定实验过程中足跟着地的各时间点,从而计算出实际步频为1.66 Hz。上述现象从一个侧面说明在步行荷载实验中记录人体运动状态的重要性。图3中实线为基准时程,虚线为拓展时程。可见,方法1、2所得时程与基准时程的波形和时长等吻合良好,而方法3、4所得结果有一定偏差。图4进一步比较了基准时程与拓展时程的功率谱特性。与时域特征吻合,方法1、2的谱线比方法3、4的谱线更接近基准时程。此外,图4清楚表明由于人行走时左右脚荷载的细微差别,造成谱线中会出现‘次谐波现象’(即在1.66Hz及其倍频间还有峰值存在),而基于左右脚荷载相同假定的时程拓展方法无法准确反映‘次谐波现象’。
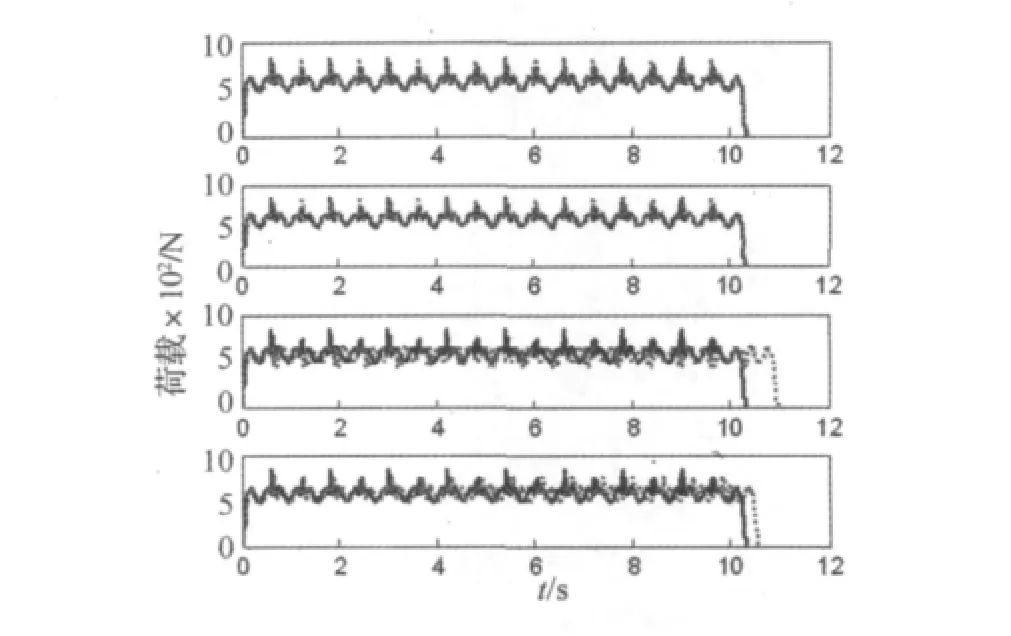
图3 各拓展时程对比(由上至下拓展方法1-4,实线:基准时程,虚线:拓展时程)Fig.3 Comparison of different expanded traces(From top to bottom:Method 1-4,Solid line:standard curve,dashed line:expanded curves)

图4 各拓展时程自功率谱对比Fig.4 Comparison of auto-spectrum of different expanded traces)
3.2 响应计算结果及分析
由各拓展时程计算得到的板中点加速度响应的均方根值见表1。由表1可见,重叠时长对拓展时程响应有很大影响;按方法1,方法2,方法4拓展时程与基准时程响应较接近,方法3的结果则误差较大。考虑到按方法1,2拓展时程与基准时程最为吻合(图3),图5给出了基准时程,按方法1拓展时程和按方法3拓展时程的加速度时程。图中峰值较大的实线为基准时程响应结果,虚线为按方法1拓展时程响应结果。
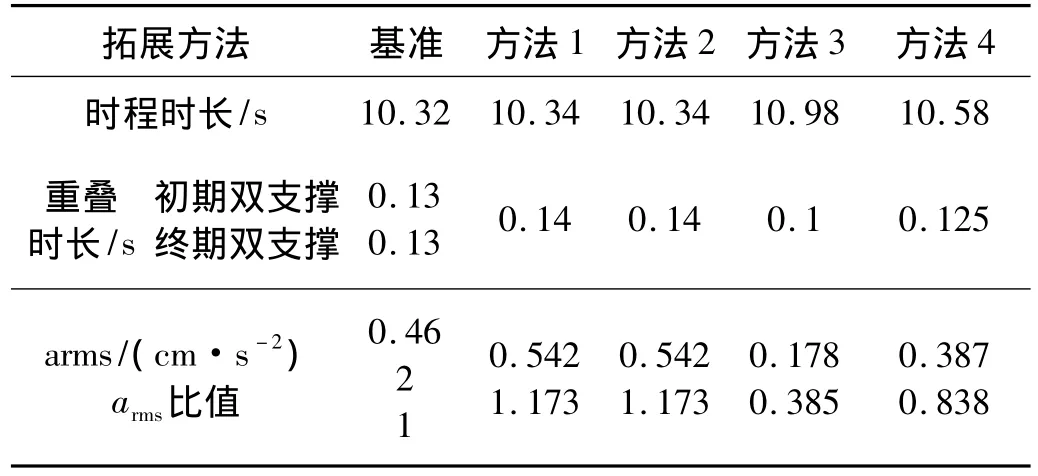
表1 各拓展时程及响应比较Tab.1 Comparison of different expanded traces and their responses
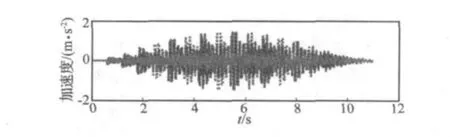
图5 3种拓展时程响应比较Fig.5 Response comparison of 3 expanded traces
3.3 板频率变化影响
振动舒适度响应分析时,步行荷载频率通常设定为楼板的倍频数以考虑最不利的共振情形。为此,取步频为 1.66、1.73、1.97、2.25 Hz四种实测基准荷载时程与拓展时程,分别计算作用于不同频率方板上的加速度响应,结果见图6~图9(图6,图8,图9中方法1与方法2结果重合)。图中横坐标为方板基频与计算步频的比值,纵坐标为各拓展时程与基准时程加速度均方根值比值。
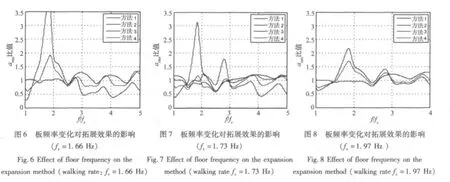
由图6~图9可见,按双支撑阶段时长拓展时程(方法3)加速度响应的误差较大(见图6~图8);按步行时间拓展时程(方法1)和按步频拓展时程(方法2)与基准时程的加速度响应最为接近;按双支撑阶段时长比例拓展时程(方法4)与基准时程加速度响应较为接近,但是在1.85倍步频处其响应有较大误差。总体上,方法1、2拓展效果较好。
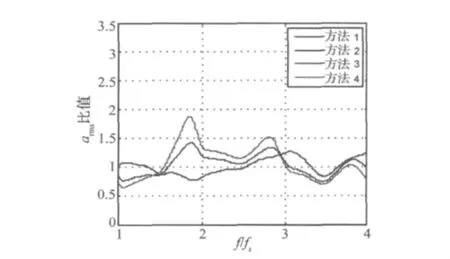
图9 板频率变化对拓展效果的影响(fs=2.25 Hz)Fig.9 Effect of floor frequency on the expansion method(walking rate fs=2.25 Hz)
3.4 拓展方法计算参数变化影响
为进一步讨论拓展方法计算参数的影响。根据以上结果,分别将方法1,方法2,方法4的参数调整 ±10%,±7.5%,±5%,±2.5%,即对方法1,分别取步行时间为 1.08,1.11,1.14,1.17,1.2,1.23,1.26,1.29和 1.32 s;对方法 2,分别取步频为 1.49,1.54,1.58,1.62,1.66,1.7,1.74,1.78 和 1.83 Hz;对方法 4,分别取双支撑阶段时长比例为18%,18.5%,19%,19.5%,20%,20.5%,21%,21.5%,22%,计算拓展时辰的加速响应。对比结果见图10~图13。
由图可见,三种拓展方法对计算参数的变化都较敏感。方法1和方法2的计算参数的变化对拓展时程加速度响应影响很大,而双支撑阶段时长比例对拓展时程加速度响应的影响则相对较小。以1.66 Hz步频数据为例(图10),按步行时间拓展时程(方法1)的arms值为 0.223 cm/s2(步行周期变化-10%),0.112 cm/s2(步行周期变化 +10%),分别为 0.542 cm/s2(真实步行周期)的0.411和0.225倍;按步频拓展时程(方法2)的arms值为0.145 cm/s2(步频变化-10%),0.285 cm/s2(步频变化 +10%),分别为 0.542 cm/s2(真实步频)的0.268和0.525;按双支撑阶段时长比例拓展时程(方法4)的arms值为0.288 cm/s2(步频变化-10%),0.495 cm/s2(步频变化 +10%),分别为 0.387 cm/s2(真实步频)的 0.743 和 1.278 倍。
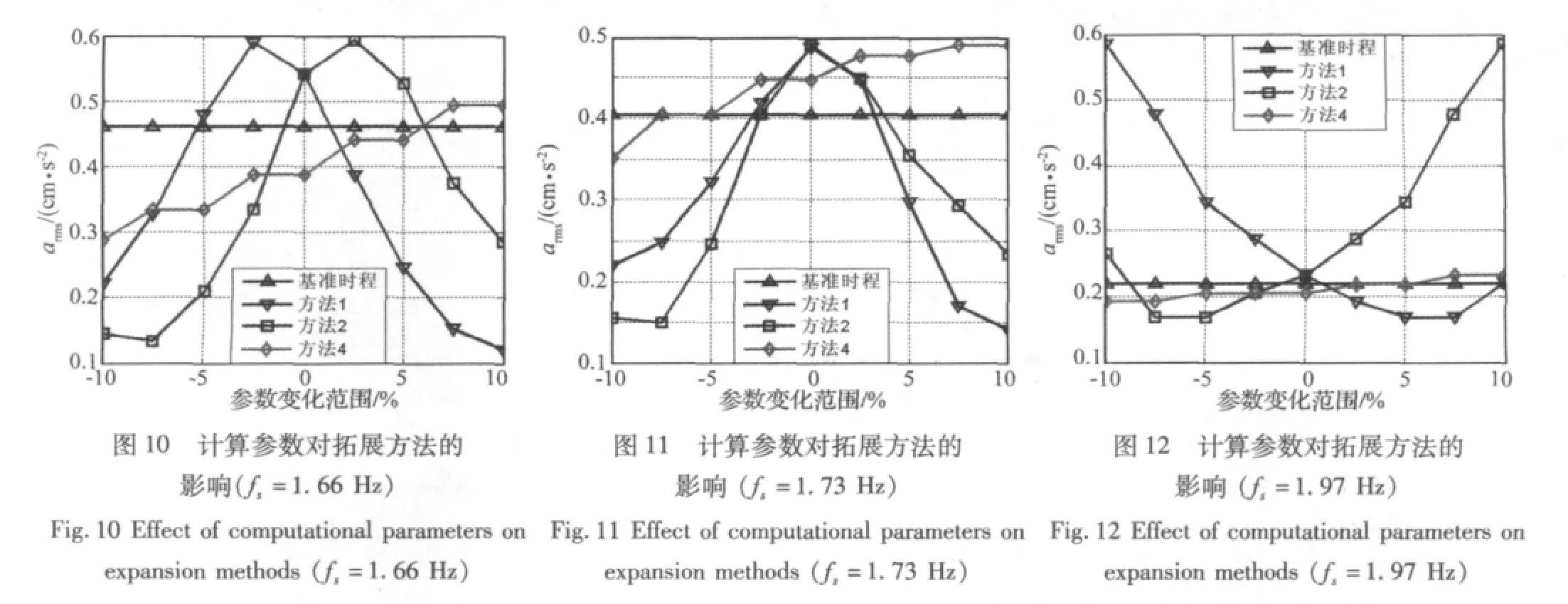
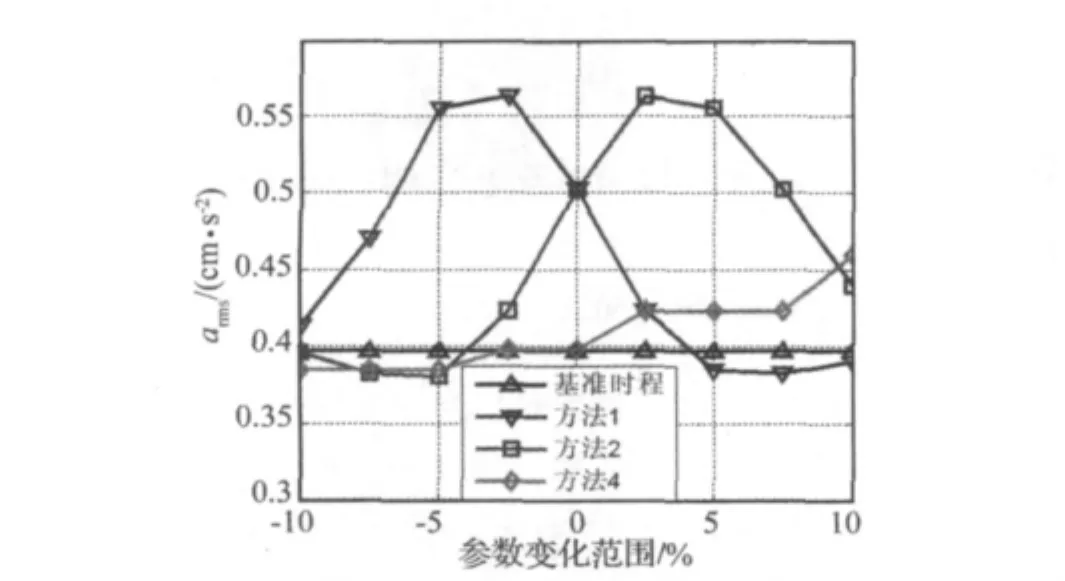
图13 计算参数对拓展方法的影响(fs=2.25 Hz)Fig.13 Effect of computational parameters on expansion methods(fs=2.25 Hz)
4 结论
研究表明按步频和按步行时间拓展所得时程及其响应与基准时程最接近,对于有确定步频或步行时间记录的实验,采用按步频或步行时间的方法拓展步行荷载时程是合理的。按双支撑阶段时长比例拓展时程响应与基准时程响应较为接近,且双支撑阶段时长比例的变化对拓展时程影响较小。在不能明确得知步频或步行时间时,由于拓展时程随步频或步行时间的变化幅度很大,不宜用按步频或步行时间的方法拓展时程,这时采用按双支撑阶段时间比例的方法拓展步行荷载时程比较合理。
在医学步态分析、运动生物力学及其他一些涉及人体运动的学科中有大量的单足落步曲线的实测资料[12],本文成果对于充分利用这些实验资料进行步行荷载动力特性的研究具有重要的指导意义。
[1] 折雄雄,陈 隽,大跨度楼盖振动舒适度研究综述[J].结构工程师,2009,25(6):144-149.
[2] 李爱群,陈 鑫,张志强.大跨楼盖结构减振设计与分析[J].建筑结构学报,2010,31(6):160-170.
[3] 樊健生,李 泉,李全旺,等.考虑人-结构相互作用的楼盖振动控制研究[J].振动与冲击,2010,29(11):230-236.
[4] 简方梁,吴定俊,李 奇.上海虹桥车站人行走廊人致振动分析[J].振动与冲击,2010,29(8):136-140.
[5] Chen J.Experiments on human-induced excitation using 3D motion capture and analysis[R].Proc.of the 3rd Asia-Pacific Young Researchers and Graduates Symposium,2011,Taipei,China,2011.
[6] Wang L,Chen J,Peng Y X,et al.Novel techniques for human-induced loading experiment and data processing[R].Proc.Of International Symposium on Innovation &Sustainability of Structures in Civil Engineering,Xiamen,2011,236.
[7] Kirtley C.Clinical gait analysis:theory and practice[M].Churchill Livingstone,2006.
[8] Kerr S C,Bishop N.Human induced loading on flexible staircases[J].Engineering Structures,2001,23(1):37-45.
[9] 宋志刚,金伟良.行走激励下大跨度楼板振动的最大加速度响应谱方法[J].建筑结构学报,2004,25(2):57-63.
[10] 刘军进,肖从真,潘宏平,等,跳跃和行走激励下的楼盖竖向振动反应分析[J].建筑结构,2008(11):108-110.
[11] Kerr S C,Bishop N.Human induced loading on flexible staircases[J].Engineering Structures,2001,23(1):37-45.
[12] Blanc Y,Blamerl C,Landio T,et al.,Temporal parameters and patterns of the foot roll over during walking:normative data for healthy adults[J].Gait& Posture,1999,10(2):97-108.

