基于循环双谱二次切片分析的滚动轴承故障诊断研究
周 宇,陈 进,董广明,肖文斌,王志阳
(上海交通大学 机械系统与振动国家重点实验室,上海 200240)
滚动轴承是机械设备中的易损零件。在使用滚动轴承的旋转机械中,大约有30%的故障是由轴承引起的。所以如何提取滚动轴承的微弱故障特征,揭示其早期、微弱、潜在故障及其发生、发展和转移,对于设备状态监测和故障诊断意义重大[1]。
近几年,研究者发现滚动轴承发生故障时,由于滚珠与滚道间的相对滑移,其振动信号的特征参数呈现周期时变的特点,即循环平稳性。国内外有很多专家对具有循环平稳性的滚动轴承故障特征提取做了研究,但主要都是集中在低阶循环平稳分析方法的研究和应用上。
在滚动轴承的早期故障监测过程中,由于微弱损伤激发的能量很小,易于淹没在背景噪声和干扰之中,使得故障信息提取的难度加大,因此采用的信号分析方法的抗噪性能将会显得尤为重要。由于高斯噪声的高阶循环统计量等于零,所以高阶循环平稳具有天然的抗噪性。
国内外已经有研究者对此做了深入的研究。先后有专家对循环双谱,即最低阶的高阶循环平稳分析方法——三阶循环累积量谱进行了深入的研究[2-4]。但是其算法所需计算量大,而且所得的最终图谱结果不直观,所包含信息的冗余量比较大。
本课题组在已经对循环双谱做了中心频率切片分析的基础上,将尝试对循环双谱进行进一步简化——对循环双谱做二次切片。也就是对循环双谱在循环频率等于信号中心频率处的切片谱再次做切片,来分析早期滚动轴承的点蚀故障。通过简化,不仅计算量大大减小,而且所得的结果也将更加直观和有效。我们将通过仿真和实验分析来论证对循环双谱做二次切片将有实际、有效的价值和意义。
1 循环双谱二次切片
1.1 循环双谱
从理论角度来说,循环平稳信号x(t)的循环双谱,是三阶循环累积量的两维傅里叶变换。
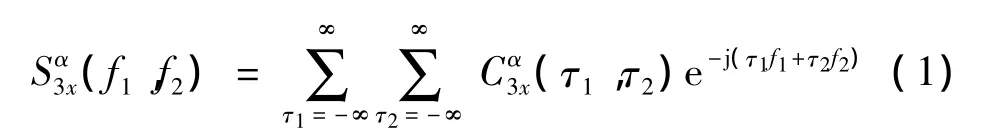
其中:α 是该信号的循环频率,τ=(τ1,τ2,…,τk-1)。对于零均值的循环平稳信号x(t),三阶循环累积量Cα3x等于三阶循环矩,即:
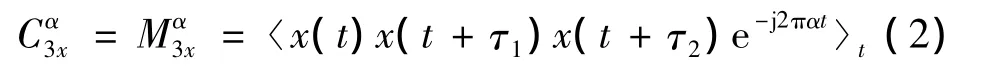
循环双谱还可以通过对使用直接算法得到的双谱引入一个循环频率 α的方法得到[2]。所以,一个离散信号x(n)的循环双谱还可以被定义为:
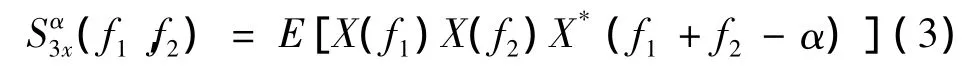
其中:x(n),n=0,1,2,…,N 是时间序列,X(f)是信号x(n)的傅里叶变换。而f,f1,f2是频率。*表示共轭。
循环双谱表示循环频率下的循环累积量的谱对双频率轴的分布。从式(3),可以看到循环双谱是个关于频率f1,f2和循环频率α的三维分布。循环双谱是个多维函数,除了利用理论推导之外,用传统的谱分析表述方法很难将循环双谱表述清楚。实际上的循环双谱是一系列对某一循环频率的循环双谱。称这样得到的某一循环频率对应的循环双谱为某循环频率下循环双谱一次切片。
某一循环频率α对应的循环双谱一次切片具有极强的对称性:

1.2 循环双谱二次切片:即循环双谱中心频率处切片谱的水平切片
由于循环双谱具有极大的对称性,图谱上重复冗余的信息比较多。另外循环双谱特定频率下的切片谱是双频率轴的三维图谱,即便做成等高线图,对于故障特征的展示也不清晰和直接。尝试按照传统的双谱的分析方法,对特定循环频率α对应的循环双谱切片做进一步的切片,使其成为一个清晰的二维图谱。对循环双谱中心频率切片谱做三种切片谱的研究:水平切片,垂直切片和对角切片。循环双谱的切片分析原理如图1所示。从图1可以直观的看到切片的研究也就是个降维的过程。

图1 循环双谱二次切片分析原理图Fig.1 The schematic diagram of the second slice of the cyclic bispectrum
首先用一个包含三个频率成分的双线性相位耦合信号来展示循环双谱的特征循环频率处切片的结果。以此来清楚地展示循环双谱某一循环频率切片图的结构特点。从而来判定应该进一步在哪个变量处做切片。
该双线性相位耦合信号为:

式中:a(t),b(t),c(t)为独立的随机窄带幅值调制,φ1,φ2,φ3是随机平稳的,且 f1+f2=f3,φ1+ φ2= φ3。取f1=1 Hz,f1=0.25 Hz。采样频率等于1。采样点数为1 024点。当循环频率α=f1,α=f2,α=f3时的循环双谱切片图分别如图2所示。

图2 当(a) α=f1,(b) α=f2,(c) α=f3时双线性相位耦合信号的循环双谱一次切片图Fig.2 Contour representation of the once slice of the CBS of the signal for
当α=f1时,循环双谱切片图上的峰值集中在(f1,f1),(f1,f2),(f1,f3),(f2,f1),(f3,f1);
当α=f2时,循环双谱切片图上的峰值集中在(f2,f2),(f2,f1),(f2,f3),(f1,f2),(f3,f2);
当α=f3时,循环双谱切片图上的峰值集中在(f3,f3),(f3,f1),(f3,f2),(f1,f3),(f2,f3)。
从图2可以看到,当循环频率α等于信号中所包含的特定频率成分时,每一个频率成分fi和循环频率α组成了一系列的频率对(α,fi)和(fi,α)。这些频率对分布在平行于频率轴的平面上,并且关于对角线对称。所以,循环双谱特定循环频率处切片谱的对角切片不能够包含所有有效的频率成分,而对其做水平切片H-H和垂直切片V-V包含所有有效的信息。另外水平切片和垂直切片存在明显的对称性,包含的信息一样,二者是等效的。故此处只做水平切片。
对于滚动轴承振动信号的循环双谱的分析,已经有前期的研究[2]证明了当循环频率等于中心频率fc时得到的循环双谱切片谱具有特殊的频谱结构,比较适用于做特征提取。
将滚动轴承循环双谱的水平切片定义为在循环双谱中心频率切片谱上经过点(α,α)的垂线的法平面。
1.3 滚动轴承振动信号的循环双谱二次切片的实现
将α=fc,f2=α代入式(3)中,则滚动轴承振动信号的循环双谱二次切片,即循环双谱中心频率切片谱的水平切片可表示为:
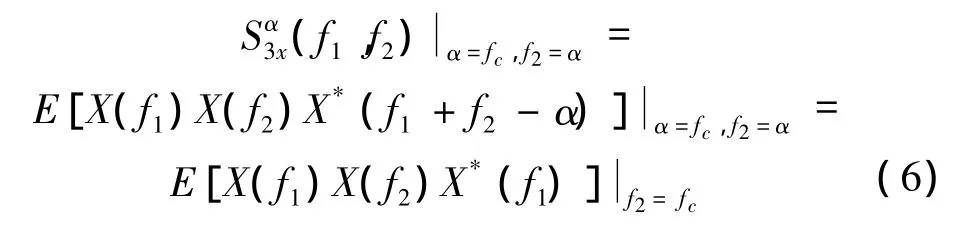
由式(6)看出,循环双谱中心频率切片谱的水平切片已经降维成一个只有一个参变量f1的两维图谱。便于直观的提取故障特征。
2 仿真分析
2.1 滚动轴承的模型
滚动轴承的工作机理使其初期故障往往表现为内圈、外圈或者滚动体上的局部点蚀。点蚀部位对与其接触的轴承其他部件产生冲击作用。定义T为冲击发生的平均周期,h(t)为点蚀故障产生的某次冲击振荡,第i次冲击的幅值为Ai。s(t)为由一系列h(t)组成的冲击串。滚动轴承的工作环境较为恶略,一般存在较强的环境噪声,因此,模型中考虑加性噪声n(t)的干扰,假定n(t)为零均值平稳随机信号。此外,由于转速的波动和滚动体所在承载区位置的不同都会引起承载角的改变,从而使得冲击周期T产生微小的改变。滚动轴承点蚀故障的信号模型为:
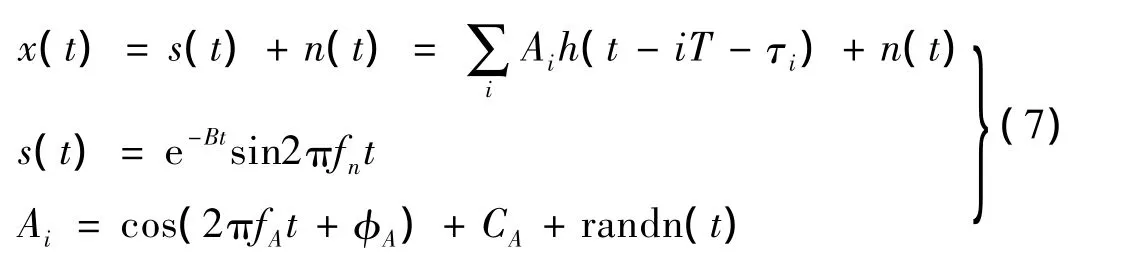
式中:τi表示第i次冲击相对于平均周期T的微小波动。φA和CA为任意常数,randn(t)为零均值的随机信号。根据故障的位置不同,{Ai}均值的调制频率fA可以为0(外圈故障),或者fA等于转频fr(内圈故障),或者fA等于保持架旋转频率fc(滚动体故障)。
2.2 仿真分析结果
当轴承外圈点蚀时,设定采样频率fs=4 000 Hz,轴承外圈通过频率为fop=50 Hz,中心频率fc=1 000 Hz。故障周期 T的微小波动{τi}的标准差 σ等于0.015 5 T。为了验证新方法对于降噪的有效性,将分别研究无噪声和信噪比SNR=10lg(σ2s/σ2n)=-13 dB的两种情况的滚动轴承点蚀故障振动信号。其中,和σ2n表示s(t)和n(t)的方差。分别将上述参数代入方程(7)有以下分析结果:
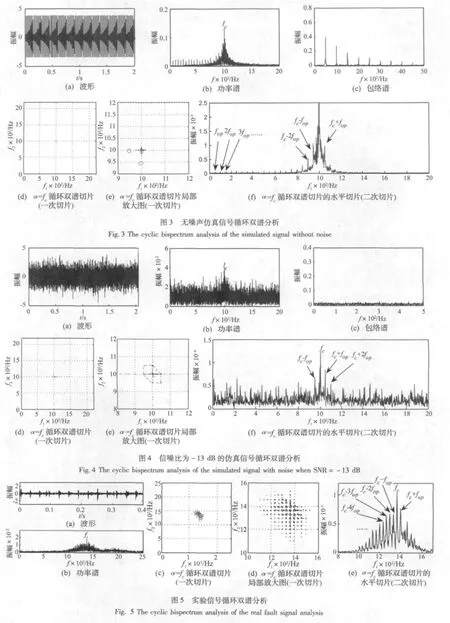
图3为无噪声的仿真信号分析。当没有噪声的时候,信号的功率谱图3(b)和包络谱图3(c)能清晰的辨识特征频率,从而确定故障类型。而从图3(f),即循环双谱的二次切片同样能有效提取出故障的特征频率。如低频段的fop,2fop,3fop和中心频率附近的fc-2fop,fc- fop,fc+fop。
图4为信噪比等于-13 dB时的仿真信号的分析结果。此时功率谱图4(b)和包络谱图4(c)都已经失效。从图4(d)可看到,在 α=fc时的循环双谱一次切片上同样可在(fc,fc)点附近找到与之间距为故障通过频率f0的六个点。这六点围绕(fc,fc)成一规则六边形结构。对这个循环双谱中心频率切片谱做经过(fc,fc)的水平切片谱,也就是对循环双谱做二次切片,如图4(f)所示。此时,在水平切片谱的中心频率两侧找到谐波成分:fc-fop,fc+fop,fc+2fop。这些个谐波成分与fc的间距为外圈故障通过频率50 Hz的一倍和两倍频成份。依次,可以判定故障的类型为外圈故障。
随着噪声的不断加大,包络谱逐渐失效。随着噪声的不断加大,信号的循环双谱中心频率切片谱的水平切片低频部分的能量成分逐渐被噪声淹没,但是在中心频率附近,由于其信噪比始终比较高,仍然能够在中心频率的左右两侧找到等间隔的谐波成分,而这些谐波成分的间距等于故障通过频率。依次可以判定故障类型。
3 实验分析
滚动轴承的实际振动信号来自于实验室的滚动轴承振动测试台,该实验台如图7所示。转子两端分别由两个滚动轴承支承,其中一个便于更换滚动轴承试件。测试台自带液压定位与夹紧装置,用于固定轴承试件的外圈。该实验台由交流电机驱动,通过联轴器带动转子运转。

图6 滚动轴承实验台Fig.6 The test bench
在测试过程中,滚动轴承的外圈固定在实验台架上,内圈随工作轴同步转动。工作轴的转速 n720 r/min。本次实验分析采用GB203的滚动轴承试件外圈点蚀故障振动加速度。试件的基本参数如表1所示。计算得到的滚动轴承故障通过频率如表2所示。

表1 滚动体结构参数Tab.1 Bearing parameters

表2 GB203滚动轴承的故障通过频率(单位:Hz)Tab.2 Character frequencies of the bearing
从该外圈故障振动信号的功率谱上可以得到中心频率fc,它对应于功率谱上最大峰值处。然后取循环双谱中心频率切片谱,如图6(c)所示。由图6(d)可以看到和仿真信号同样的结论:围绕 (fc,fc)点,有一个以上的六边形结构分布的点阵,这些点阵距离中心点的距离为故障通过频率fop的倍频。但是这样的结果还是不够直观,而且图谱上面点阵比较复杂,如果不仔细分析难以直接提取出故障特征。而从图6(e),对循环双谱的中心频率切片谱做水平切片,即做该故障信号的循环双谱的二次切片。在二次切片图上,看到在中心频率两侧分别有一系列的谐波成分:fc-4fop,fc-3fop,fc-2fop,fc-fop,fc+fop。得到这些特征频率成分,也就可以判定故障类型了。由此,对该信号的循环双谱做二次切片可以得到更加清晰、直观的故障特征提取结果。
4 结论
通过上述的分析知,当滚动轴承产生早期故障时,由于微弱损伤激发的能量很小,被淹没在背景噪声和干扰中。此时,由于中心频率处具有相对较高的信噪比,应用循环双谱的二次切片,即循环双谱的中心频率切片谱的水平切片能够有效抑制噪声的干扰。在此切片的高频部分的中心频率两侧均匀分布着间隔为故障通过频率的谐波。可借由此特点做故障特征的提取。其优越的抗噪性及较少的计算量使得该方法在旋转机械领域具有广阔的应用前景。但是也存在着一定的缺陷,即在实际中振动信号的噪声比较大的情况下,如果在功率谱上没有显著的中心频率峰值,中心频率的确定比较困难。可以尝试采用加速度传感器的共振频率作为轴承振动信号的中心频率来做切片分析。当然,这只适用于一阶振动系统,将在以后的研究中仔细的探讨这一问题。
[1] 陈 进.旋转机械设备状态监测与故障诊断[M].上海:上海交通大学出版社,1999.
[2] GardnerW A, Spooner C M. Cumulanttheory of cyclostationary time-series,part I:foundation[J].IEEE Transactions on Signal Processing,1994,42:3387-3408.
[3] McFadden P D,Smith J D.Model for the vibration produced by a single point defect in a rolling element bearing[J].Journal of Sound and Vibration,1984,96:69-82.
[4] Antoni J,Randall R B.A stochastic model for simulation and diagnostics of rolling element bearings with localized faults[J].Journal of Vibration and Acoustics,Transactions of the ASME,2003,125:282-289.
[5] Yiakopoulos C T,Antoniadis I A.Cyclic bispectrum patterns of defective rolling element bearing vibration response[J].Forschung im Ingenieurwesen/Engineering Research,2005,70:90-104.
[6] Zhu Z K,Feng Z H,Kong F R.Cyclostationarity analysis for gearbox condition monitoring:Approaches and effectiveness[J].Mechanical Systems and Signal Processing,2005,19:467-482.
[7] SpoonerC M, Gardner W A. Cumulanttheory of cyclostationary time series, part Ⅱ:developmentand applications[J].IEEE Transactions on Signal Processing,1994,42:3409-3429.

