结构支撑位置改变时固有频率的快速计算

欧阳炎，王 栋

(西北工业大学 航空学院 结构动力学与控制研究所，西安 710072)

在结构动力学优化设计过程中，为了获得满意的动态响应，需要对结构进行反复修改和设计，其动力学特性的重新分析就不可避免。一般情况下，每次修改后，需先对结构重新进行网格划分，然后计算结构的固有特性，这是造成结构优化设计时间过长，效率低下的一个主要原因。为了减少有限元重复分析次数，降低优化过程中的计算成本，动响应计算技巧和方法需给予足够的重视，对于大型复杂结构的动力学问题有必要寻求快速的计算方法［1］。一种行之有效的策略是充分利用优化设计过程中的中间结果，不用直接求解结构修改后的特征方程，根据已得到的结构动态特性，快速、准确地计算模型修改后结构的动态特性，从而有效地减少动力学重分析的次数［2］。

在实际工程设计中，常利用附(增)加支撑(承)的方法来提高结构的刚度和固有频率，避免产生危险的共振现象。有关梁、薄板结构附加支撑的位置和刚度的优化设计研究，已有许多成果［3－7］。现有的研究成果表明［4－7］:为了提高结构的第一阶固有频率值，附加支撑的最优位置并非总是在有限元网格的节点上，有可能出现在单元的内部。

文献［7］提出利用插值技术代替网格细化以及特征值求解计算。由于固有频率对支撑位置的函数毕竟是相当复杂的隐函数，而梁的插值函数仅是位置坐标的3次多项式函数，板的插值函数是位置坐标的(交叉)4次多项式函数，因此人们不禁会对插值计算固有频率所得结果的精度和适应性产生疑问。本文着重探讨支撑位于单元内部时，细长梁和薄板结构固有频率快速计算方法的精度和适应性问题。

1 支撑刚度等效方法

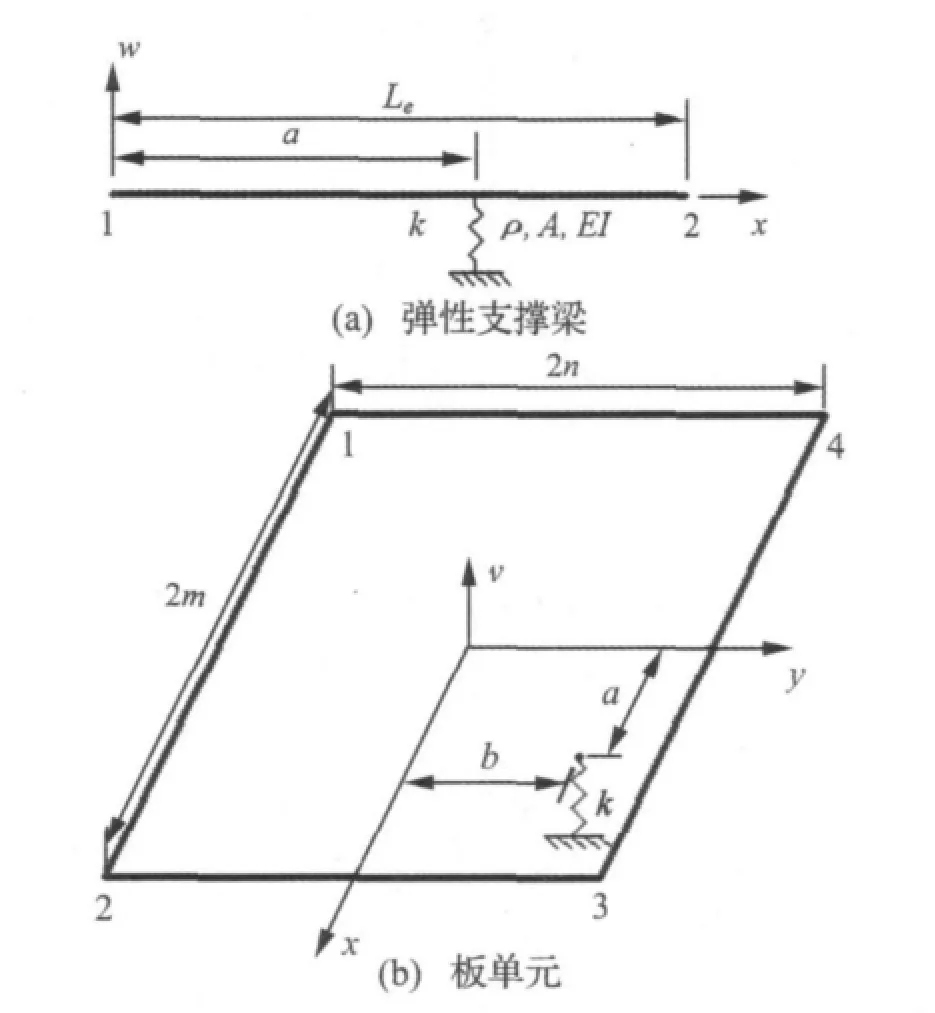
图1 单元内部有一个弹性支撑的梁、板单元Fig.1 A beam or plate element with an elastic support

如图1所示，梁、板单元内部附加有一个弹性支撑。若只考虑支撑的横向线刚度，并忽略其自身的质量。则支撑的单位等效刚度矩阵Ks只是支撑位置的函数，可由单元的位移形状函数表示为［6］:

其中，N(a)和N(a，b)分别是梁和板单元的形状函数矩阵。2节点4自由度梁单元的形状函数为［9］:

N(ξ)= ［N1N2N3N4］T

其中:

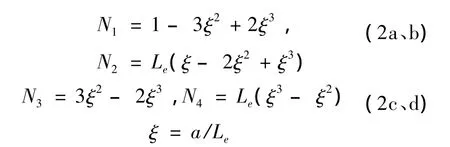
4节点12自由度矩形薄板单元的形状函数矩阵N(a，b)见文献［9］。在结构有限元网格不变的情况下，将附加支撑的等效刚度矩阵与结构的刚度矩阵叠加，则系统的频率特征方程可写成:

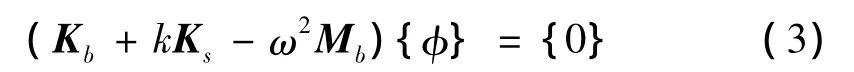
其中，k是支撑的线性刚度系数，Kb、Mb分别为梁或板结构的刚度矩阵和质量矩阵。通过求解特征值问题(3)便可计算出总体结构的固有频率值ω。可见这样处理弹性支撑后，求解的特征值问题阶数不变。而且Kb和Mb不受支撑位置变化的影响。

“科学是人类认知世界不竭的长河，技术是人类对生存发展方式不倦的创造.研究科学史，本质上也就是研究人类创造的历史，继往而开来，有着十分重要的价值和意义.”

2 利用形函数插值方法

对于梁或框架结构，第i阶固有频率ωi相对于支撑位置a的一阶导数可表示为［7］:

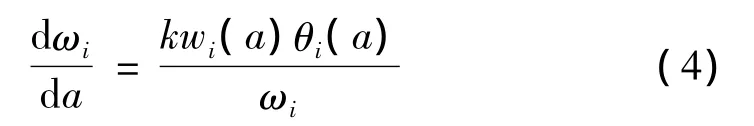
其中，wi(a)和θi(a)分别为第i阶振型在支撑节点处的位移和转角，而且振型已按质量正交归一化处理。在计算出弹性支撑位于单元节点上的第i阶频率和对支撑位置的一阶导数后，利用梁单元自身的形状函数N1～N4，可以用插值计算当支撑位于单元内部a处时(如图1(a)所示)的频率值:

对于薄板单元，支撑在单元内部的位置如图1(b)所示。与梁单元类似，可得第i阶频率关于支撑位置的灵敏度为［7］:

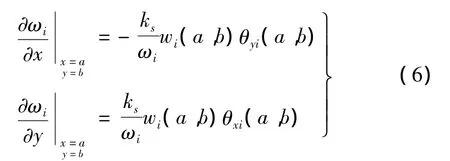
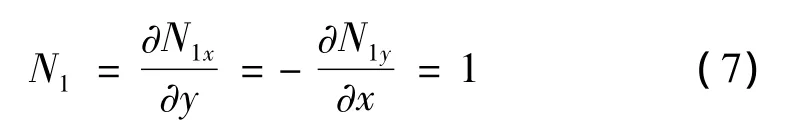
可得到支撑位于该单元内部任意点(a，b)处，结构的第i阶固有频率:

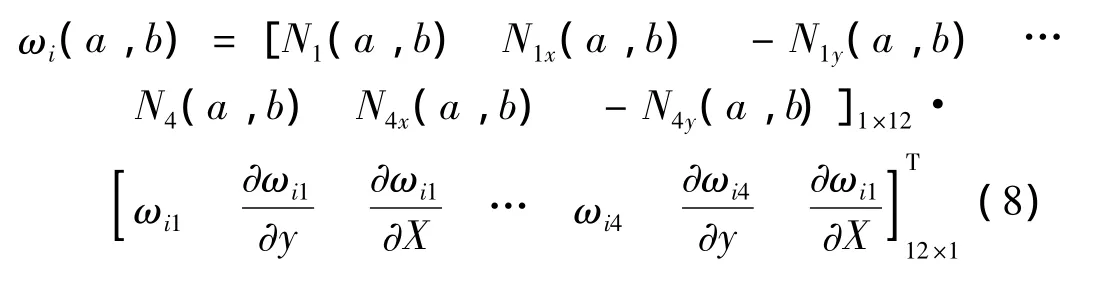
其中，wi(a，b)，θxi(a，b)，θyi(a，b)分别为第 i阶振型在支撑点(a，b)处的位移、绕x轴转角和绕y轴转角。与梁单元类似，在计算出支撑位于单元节点上时的第i阶频率ωi1～ωi4以及频率关于支撑位置的灵敏度后，利用板单元自身的形函数N1～N4y，并结合形函数在节点上的特性，例如在节点1处有:

利用单元形函数插值法计算固有频率无需求解特征值问题，仅仅是一些代数运算，因而计算效率更高。由于附加支撑的刚度值和位置会对结构的频率和振型产生影响，在利用式(5)或式(8)计算固有频率时，必须考察支撑位于不同节点处时的振型是否一致。

3 数值算列

为了对比两种方法计算结构固有频率的精度和效率，将两种方法用Matlab®编程，分别计算梁和薄板结构附加弹性支撑后的第一阶固有频率值。

3.1 附加弹性支撑的梁结构

如图2所示悬臂梁，截面为正方形，边长1 cm，长度L=1 m，密度 ρ=7 800 kg/m3，弹性模量 E=200 GPa。将结构分为10个2节点4自由度梁单元。分别取弹性支撑的刚度系数 k1=3.74 kN/m、k2=16.67 kN/m和k3=44.48 kN/m。根据上述两种方法，分别计算支撑位置b在梁上连续移动时，悬臂梁第一阶固有频率值，变化曲线如图3所示。从该图中可以看出，当弹性支撑在整个梁跨度之间移动时，具有较小刚度值(k1、k2)的支撑采用插值方法计算结果与等效刚度法所得结果基本一致。从计算效率方面来看，支撑正好在网格节点处时进行9次特征值计算后，支撑点位于单元内部时，刚度等效法要再进行多次的特征值求解计算，而插值方法由代数运算即可得出结果。

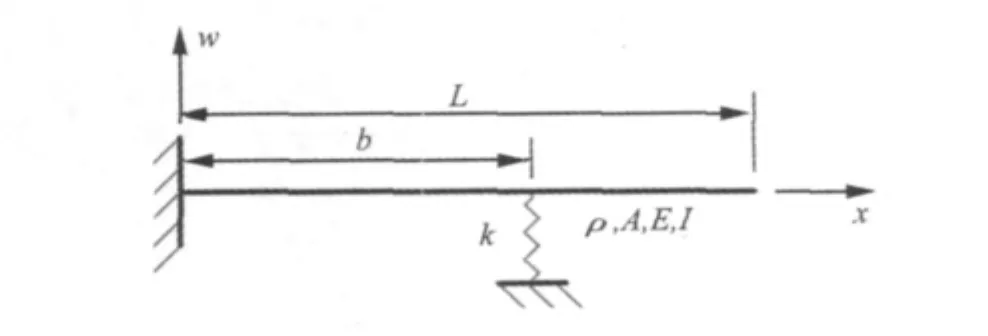
图2 附加一个弹性支撑的梁结构Fig.2 A cantilever beam with an elastic support

当支撑的刚度值较大为 k3，并位于区间(0.7，0.8)m时，两种方法计算结果与理论分析方法［10］所得结果列于表1。从表中可以看出，支撑刚度等效方法与理论解符合较好，计算精度较高。

由文献［5］中结论结合本文算例的数据可知，当k3=44.48 kN/m，b=0.783 4 m 时，附加弹性支撑可使悬臂梁的第一阶频率值上升到原结构(无支撑时)的第二阶频率。当弹性支撑分别位于相应单元的两侧节点上，即b=0.7 m和b=0.8 m时，悬臂梁的第一、第二阶振型如图4所示，从图中可以看出，支撑在单元两侧节点处时，第一阶振型发生了改变。则根据灵敏度公式(4)计算频率的一阶导数时，对应的振型不同，利用插值公式(5)计算所得结果会有一定的误差。这是造成图3中两种方法所得结果局部不完全相同的原因。由表1可以看出，越靠近单元中间，方法2的误差越大。

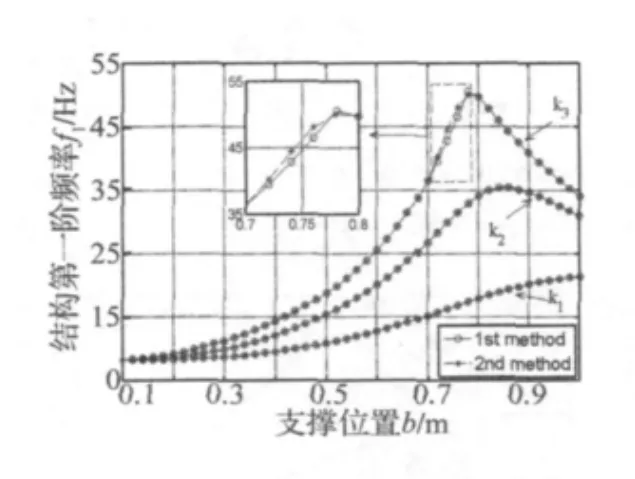
图3 悬臂梁第一阶频率随支撑位置b的变化Fig.3 Variations of the 1st frequency of the cantilever beam versus the support position b

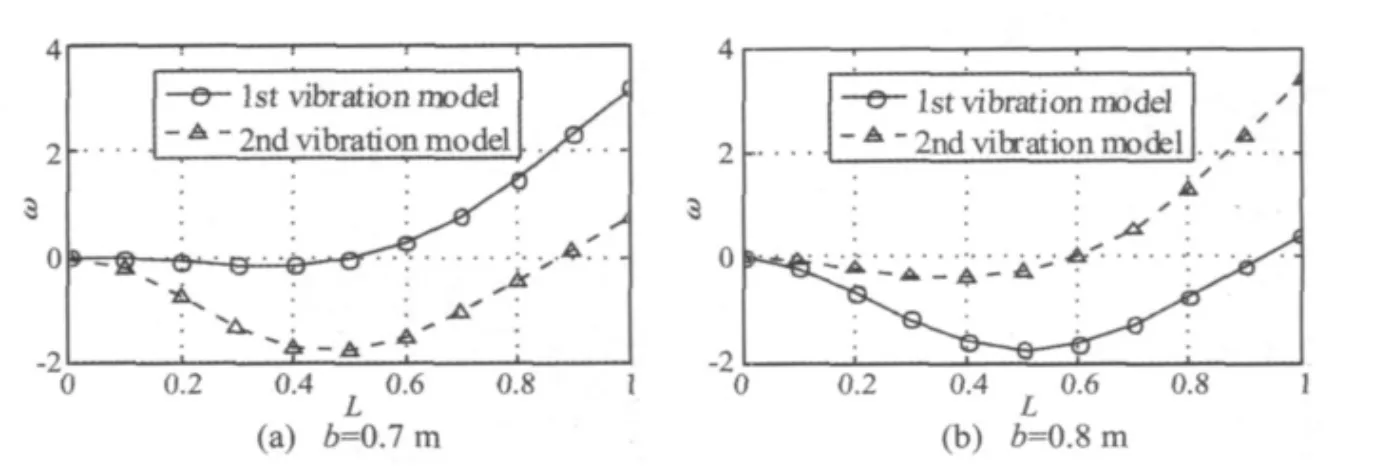
图4 刚度为k3的支撑位于不同节点时悬臂梁的前两阶振型Fig.4 The 1st and 2nd vibration mode shapes of the cantilever beam with an elastic support of stiffness k3located at different nodes

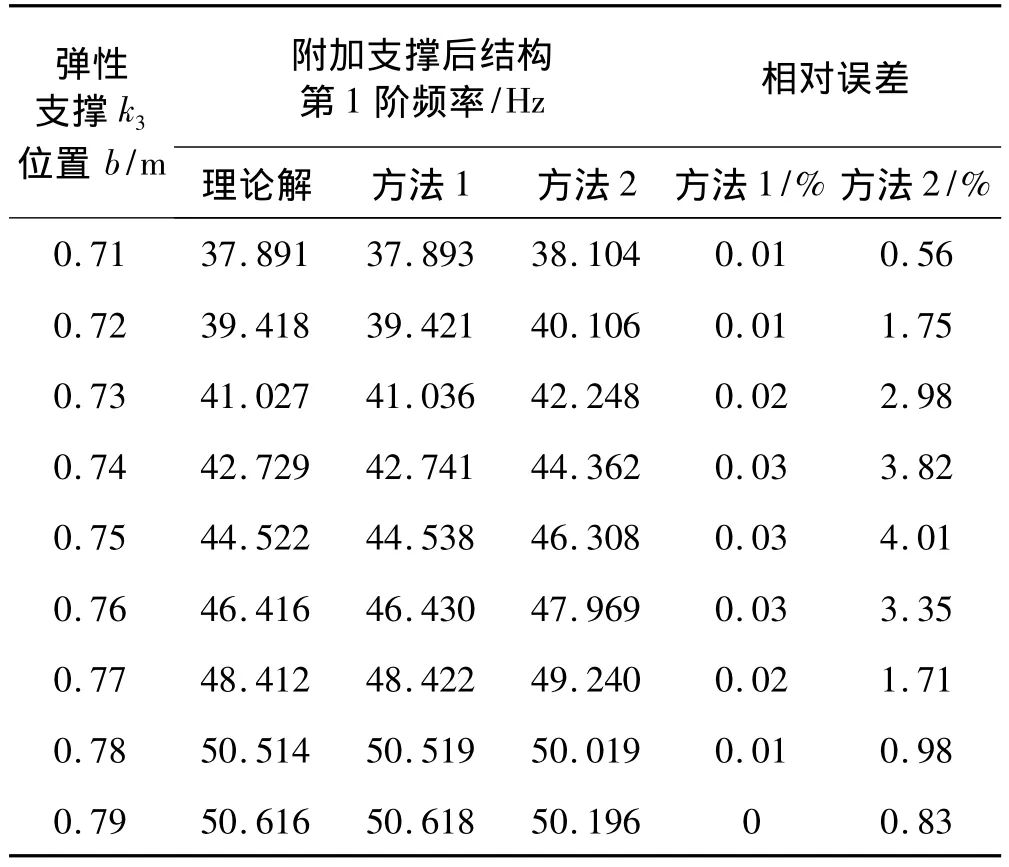
表1 附加弹性支撑悬臂梁的第一阶频率值Tab.1 The 1st frequency of the cantilever beam

3.2 附加弹性支撑的悬臂板结构

如图5所示正方形悬臂板［7］，边长 L=W=305 mm，厚度 h=3.28 mm，泊松比 μ =0.3，密度 ρ=2 821 kg/m3，弹性模量E=73.1 GPa。采用4节点12自由度矩形薄板单元，将悬臂板划分成10×10个单元。

在自由边上对称地布置两个相同刚度的弹性支撑。当支撑数较多时，公式(6)可写成对多个支撑灵敏度值相加的形式。图6显示了不同支撑刚度值时，悬臂板第一阶固有频率随支撑位置a的变化关系。其中，k1=25.39 kN/m，k2=50.79 kN/m，从图中可以看出，支撑刚度为k1时，两种快速计算方法结果基本一致。然而刚度等效方法在处理支撑位于单元内部时，要多次求解高阶矩阵(本文为330阶)的广义特征值，因此计算效率很低。

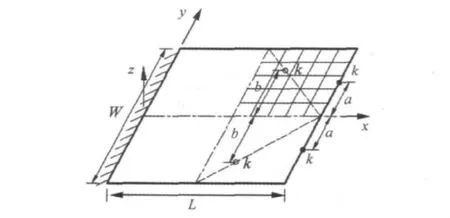
图5 附加两个弹性支撑的矩形悬臂板结构Fig.5 A cantilever plate with two elastic supports

当支撑刚度为k2，支撑位置a/W在区间［0.1，0.2］上时，两种方法所得结果有一定的误差。当支撑位于 a=30.5 mm(a/W=0.1)，和 a=61 mm(a/W=0.2)时，悬臂板的振型分别如图7所示。可知悬臂板的第一阶振型由扭曲振型转变为弯曲振型，则由式(6)计算得到的灵敏度所用的振型完全不同，因而由式(8)插值计算得出的频率值与真实值之间有一定误差。

在不同的刚度值下，悬臂板的第一阶扭曲振型和第一阶弯曲振型对应的频率与支撑位置a的关系如图8所示。从图中可以看出，当支撑刚度为k1，a在整个区间上变化时，悬臂板的第一阶频率始终对应第一阶弯曲振型，故两种方法结果吻合很好。当支撑刚度为k2，a在区间［30.5，61］mm时，结构的第一阶频率对应的振型由扭曲振型逐渐变为弯曲振型，即结构的振型在a=30.5 mm和a=61 mm时发生了根本性改变，所以两种方法的计算结果有误差，其中支撑刚度等效方法的结果较准确。而当a＞61 mm时，第一阶频率对应振型保持不变，两种方法计算结果基本一致。

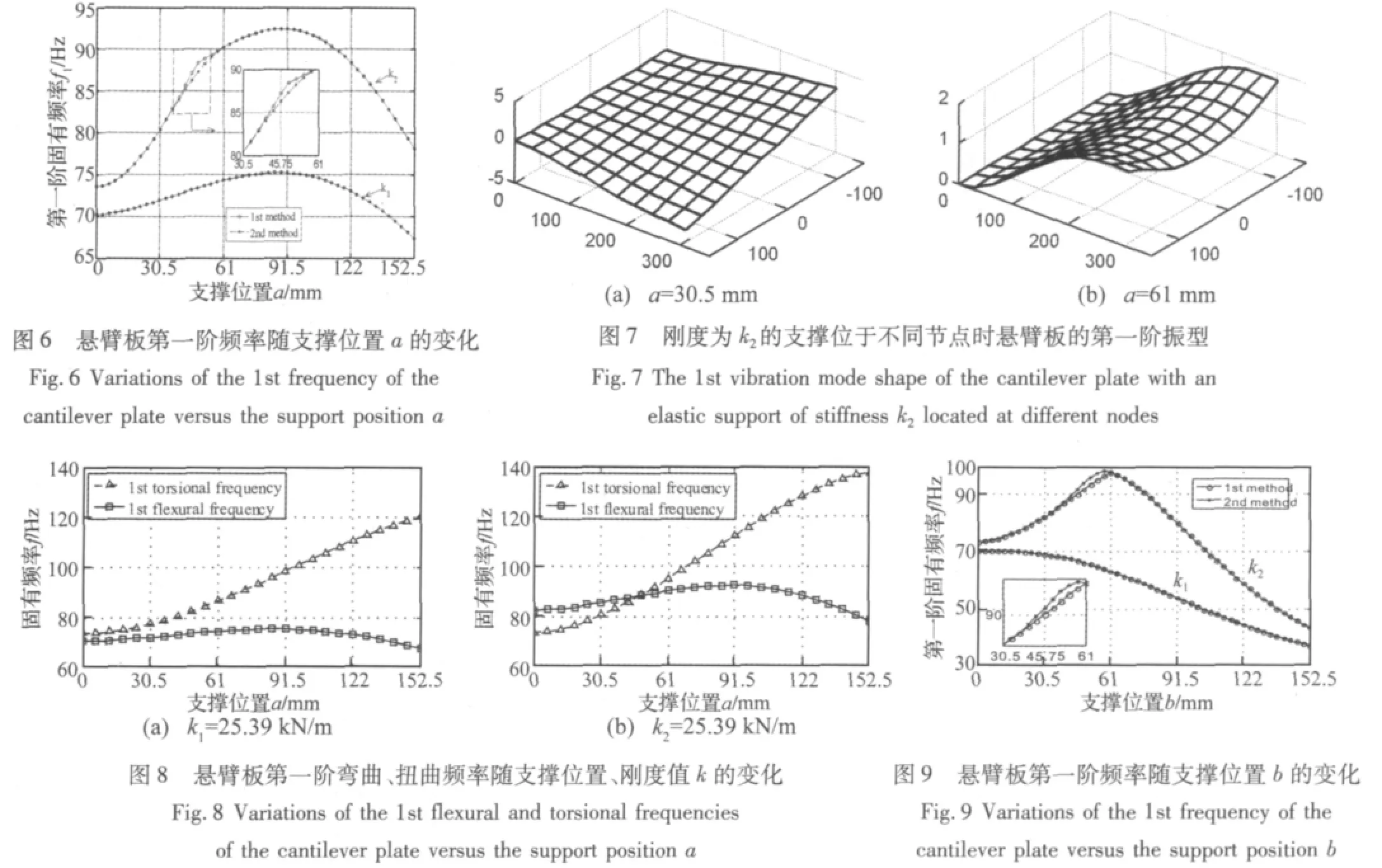
作为对比，若使两个刚度相同的弹性支撑沿单元的对角线方向移动，如图5中虚线所示，支撑位置与悬臂板第一阶固有频率关系如图9所示。其中，k1=25.39 kN/m，k2=76.18 kN/m，从图中可以看出，支撑刚度为k1时，两种方法计算结果基本相同。由于插值方法只需在支撑移动轨迹上不同单元的节点处进行少数几次特征值求解，因此，其计算效率更高。

当支撑刚度为 k2，支撑位置 b/W 在区间［0.1，0.2］，即支撑移动轨迹的第2个单元内时，两种方法的计算结果有明显差别。这同样是由于悬臂板的第一阶振型发生改变的结果。其中，支撑刚度等效方法的结果较准确，插值计算结果有一定的误差。

4 结论

用有限元法计算附有弹性支撑的梁、板结构固有频率时，如果支撑位置移动到了单元的内部，应用支撑刚度等效或插值方法，都无需重新划分网格，可以避免因网格变化对计算精度造成的影响。其中，刚度等效法在不增加求解阶数的情况下，通过解特征值问题获得结构的固有频率。插值法用单元的形函数和固有频率的导数值计算支撑在单元内部时的频率值，充分利用了前期的计算结果，因此效率较高。

当弹性支撑的刚度相对较小时，两种方法的计算结果吻合良好，且都有较高的精度。当支撑刚度较大时，在结构的某些单元节点位置处，结构对应于同一频率的振型将发生改变，导致频率关于支撑位置的灵敏度计算公式应用了不同振型的响应值。由此引起利用形函数插值法计算结果会有一定误差，使用时必须首先加以判断。支撑刚度等效法无此限制，故应用范围更广。

在实际应用中，可充分利用两种方法各自的优点，将两种方法结合使用，即在振型可能有突变的单元处，用支撑刚度等效法计算结构的固有频率，保证计算结果的精度。而在振型无突变的其他单元处，则可考虑用形函数插值方法，以提高计算速度。

［1］ Su H C，Feng R.A new method of structural modal reanalysis for topological modifications［J］.Finite Elements in Analysis and Design，2002，38:1015－1028.

［2］ 何建军，姜节胜，康兴无.结构拓扑大修改的动力学重分析方法［J］.振动工程学报，2007，20(4):407－411.

［3］ 宋 华，胡 瑞，任辉启，等.内部为弹性点支承的简支板的振动分析［J］.地下空间与工程学报，2007，3(4):613－616.

［4］ 燕乐维，陈树辉.一种改进的广义遗传算法及其在结构动力优化问题中的应用［J］.工程力学，2010，27(5):21－26.

［5］ Wang C Y.Minimum stiffness of an internal elastic support to maximize the fundamental frequency of a vibrating beam［J］.Journal of Sound and Vibration，2003，259(1):229－232.

［6］ Friswell M I，Wang D.The minimum support stiffness required to raise the fundamental natural frequency of plate structures［J］.Journal of Sound and Vibration，2007，301:665－677.

［7］ Wang D，Jiang J S，Zhang W H.Optimization of support positions to maximize the fundamental frequency of structures［J］. International Journal for Numerical Methods in Engineering，2004，61:1584－1602.

［8］ 李 涛，左正兴，廖日东.结构仿真高精度有限元网格划分方法［J］.机械工程学报，2009，45(6):304－308.

［9］ 朱伯芳.有限单元法原理与应用(第三版)［M］.北京:中国水利水电出版社，2009.

［10］ 方 同，薛 璞.振动理论及应用［M］.西安:西北工业大学出版社，1997.