冷弯薄壁型钢-稻草板组合楼盖抗振性能1)

张秀华 赵梓霖 孟毅豪 张华鹏 马彦龙

(东北林业大学，哈尔滨，150040)

随着中国住宅产业化进程的加快，新型建筑材料与组合形式日新月异。轻钢组合结构体系轻质高强、施工快速环保，具有良好的保温性和抗震性，在国内外住宅建筑中得到了广泛的应用。但由于轻钢结构自重轻、刚度小，自振频率较低，在使用过程中很容易发生振动，达到一定程度时会影响人的日常舒适度，因此，楼板抗振舒适度问题成为结构工程设计中常常要面对的问题。国内外学者进行了有关抗振舒适度的研究。美国学者Murray[1]研究得出，人们对5～8 Hz频率的振动特别敏感，因为，人体在这些频率中产生共振。Kraus et al.[2]、Zhao et al.[3]针对刚性支撑件布置形式、楼盖梁跨中处开洞、墙体作用以及抗剪连接程度等因素对楼盖抗振性能影响做了相应的研究。周绪红等[4]、李颖[5]、管宇等[6]研究了边界条件对钢-木(OSB板)组合楼盖刚度、频率及挠度的影响，在轻型组合楼盖舒适性方面取得了阶段性的成果。

通过查阅相关文献[7-8]和现行的中国规范JGJ3-2010《高层建筑混凝土结构技术规程》[9]、GB50010-2010《混凝土结构设计规范》[10]及CECS 273-2010《组合楼板设计与施工规程》[11]中只有对混凝土组合楼盖抗振频率有明确规定，对于轻钢组合楼盖抗振舒适度尚无明确的设计方法和评价标准。为便于轻钢组合结构房屋的推广，完善这类楼盖的设计理论是十分必要的。

为丰富轻钢组合楼盖的形式，文中提出一种由冷弯薄壁C型钢作为楼盖梁、上覆纸面稻草板并通过自攻螺钉和抗剪连接件组成的新型冷弯薄壁型钢-稻草板组合楼盖。张秀华等[12]对轻钢-稻草板组合楼板进行了研究，得出轻钢-稻草板组合楼板具有良好的承载力、刚度，满足建筑结构的要求，表明纸面稻草板作为轻钢组合楼板覆面板是可行的。

为进一步研究冷弯薄壁型钢-稻草板组合楼盖抗振性能。对2块单跨冷弯薄壁型钢-稻草板组合楼盖的静载试验和动载试验研究，并进行有限元参数分析及理论分析，结合现有标准科学评价其舒适度，提出该组合楼盖自振频率的简化计算公式，为冷弯薄壁型钢-稻草板组合楼盖在轻钢结构中的应用与推广提供理论依据。

1 材料与方法

1.1 试件设计

为研究冷弯薄壁型钢-稻草板组合楼盖抗振性能，根据《低层冷弯薄壁型钢房屋建筑技术规程》[13]共设计2块组合楼盖试件，平面尺寸为2 400 mm×1 200 mm，板跨为2 200 mm。

组合楼盖由纸面稻草板(简称稻草板)与型钢骨架通过ST4.8级自攻螺钉连接，楼盖四周螺钉间距为150 mm，中间螺钉间距为300 mm。稻草板尺寸为2 400 mm×1 200 mm×58 mm。型钢骨架由Q235B级镀锌钢板冷弯成型的C型钢与U型钢通过长为16 mm的ST3.5沉头自攻螺钉连接组成。第一块楼盖试件ZHB-1楼盖梁为C150 mm×50 mm×20 mm×1.5 mm，间距为600 mm，边梁为U153 mm×50 mm×1.5 m；第二块楼盖试件ZHB-2楼盖梁为C120 mm×40 mm×15 mm×1.5 mm，间距为400 mm，边梁为U123 mm×40 mm×1.5 mm。以试件ZHB-1为例，尺寸及构造见图1。

1.2 材料力学性能

根据GB/T228.1-2010《金属材料拉伸试验第Ⅰ部分：室温试验方法》[14]的规定进行材性试验，得出钢材屈服强度为274.3 MPa，抗拉强度为372.7 MPa，弹性模量为198.3 GPa。

根据GB/T31264-2014《结构用人造板力学性能试验方法》[15]进行材性试验，得出所用稻草板(沿长度方向)抗弯强度为1.87 MPa，弹性模量为400.6 MPa。

1.3 试验加载装置及加载制度

组合楼盖为两边支撑、梁端简支，故将楼盖放置在铰支座上，铰支座下方为刚性支墩。测量楼盖挠度和自振频率时，共5种加载方式：测量1 kN集中荷载作用于跨中时的挠度采用1 kN砝码集中加载(图2a)，数据由DH3816N采集系统采集;体重为80 kg的男子分别沿平行于楼盖梁和垂直于楼盖梁方向行走(图2b)；重为10 kg的沙袋从距楼盖中心0.33 m处自由下落(图2c)；体重为80 kg的男子在楼盖中心身体前倾脚后跟抬高50～60 mm重重落下冲击楼盖(图2d)；综合参考文献[4-7]中的试验方法，采用激励锤在楼盖中心点位置、沿着楼盖跨度和宽度1/4位置等多处位置锤击进行激振，持续1 min左右(图2e)。图2b、图2c、图2d、图2e加载方式下的数据由东华DH5922动态采集系统采集，采样频率为200 Hz，采样持续时间约5 s。

1.4 测点布置

试件均为对称结构，为测得组合楼板挠度和自振频率，测点布置见图3。试件试验时测点布置图见图3。位移计测量组合楼盖挠度，加速度传感器测量组合楼盖自振频率。

1.5 计算方法

国内对轻钢组合楼盖舒适度没有明确的评价标准与计算方法。对此借鉴了多个国家学者提出的相应准则，综合评价冷弯薄壁型钢-稻草板组合楼盖的舒适度问题。

1 kN静力荷载作用于楼盖跨中时挠度按瑞典与澳大利亚标准进行计算。

瑞典Ohlsson准则[16],假定集中荷载直接作用在楼盖梁上。在1.0 kN静态集中荷载作用下，单个楼盖梁挠度应限制在1.5 mm。楼盖梁的挠度由下式计算得出：

(1)

式中:δP为楼盖跨中挠度，mm；P为集中荷载，P=1 kN；L为楼盖梁跨度，mm；E为楼盖梁弹性模量，N·mm-2；Ix为单根楼盖梁惯性矩，mm4。计算简图如图4b。

澳大利亚准则[17],1 kN集中荷载作用在楼盖任何位置时，楼盖挠度小于2 mm。楼盖梁跨中挠度由下式计算：

(2)

楼盖的自振频率按瑞典Ohlsson准则与美国Johnson准则进行计算。

瑞典Ohlsson准则要求楼盖的自振频率大于8 Hz，本楼盖属于单向板，故楼盖的自振频率由下式计算：

(3)

式中:f为楼盖自振频率，Hz；Dx为平行于楼盖梁方向楼盖刚度(Dx=EI/s)，N·mm-1；g为楼盖单位面积自质量，N·mm-2；L为楼盖梁跨度，mm；s为楼盖梁间距，mm。计算简图如图4a。

美国Johnson准则[18]要求楼盖的自振频率大于15 Hz，忽略覆面板，仅考虑单个楼盖梁的惯性矩。楼盖的自振频率由下式计算：

(4)

式中:f为楼盖自振频率，Hz；g为重力加速度，9.8m·s-2；E为楼盖梁弹性模量；Ix为单个楼盖梁惯性矩；W为楼盖自质量，N；L为楼盖梁跨度，mm。计算简图如图4b。

2 结果与分析

2.1 试验结果

2块组合楼盖各工况下加速度-频率曲线如图5所示。图5中第一个加速度峰值对应的频率为试件的自振频率。各组合楼盖的自振频率取5种工况的平均值。试验结果如表1所示。试件ZHB-1的自振频率为27.59 Hz，试件ZHB-2的自振频率为22.37 Hz。

表1 荷载工况及试验结果

注：荷载工况中A代表1 kN静力荷载作用于楼盖中心；B代表人沿平行于楼盖梁方向行走；C代表人沿垂直于楼盖梁的方向行走；D代表10 kg沙袋从0.33 m空中落下冲击；E代表脚跟冲击；F代表激励锤冲击。

由表1可知，该组合楼盖在1 kN集中荷载作用下静力挠度均小于2 mm，自振频率均大于15 Hz，满足国外相关规范要求[16-18]。试验结果表明，在相同用钢量下，减少楼盖梁数量、增大梁截面尺寸，楼盖跨中挠度减小，自振频率增大。

2.2 有限元数值分析

在前期研究中，做了大量稻草板组合楼板和组合墙体的试验，在此基础上进行了有限元分析，有限元计算结果与试验结果吻合较好，验证了有限元的可行性，为后续有限元分析提供参考依据。

2.2.1 有限元模型验证

为了进一步验证有限元数值分析的可靠性，对试验模型采用有限元软件ANSYS进行数值分析。钢材和稻草板使用Shell181单元模拟，覆板与骨架间连接作用通过耦合方式进行模拟。试验过程中组合楼盖变形发生在弹性阶段，故钢材和稻草板的本构关系采用线弹性模型。网格划分采用映射的方法，钢材和稻草板3个方向单元长度均为25 mm。组合楼板约束同试验的实际情况一致，即两端的约束采用的是简支约束。施加荷载时按照试验情况在组合楼板上部进行加载。

将试验楼盖与其相应的有限元模型竖向挠度值和不同振型自振频率进行对比，挠度值对比结果见表2，前3阶自振频率对比结果见表3。

表2 试验与有限元分析挠度值

由表2和表3可知，跨中挠度分析结果与试验结果误差在15%以内，自振频率分析结果与试验结果误差为10%以内，验证了有限元的可行性，为后续分析提供依据。总结二者存在误差的原因是，有限元的边界条件和材料本构关系设置较理想化；使用耦合模拟自攻螺钉连接作用存在一些弊端。

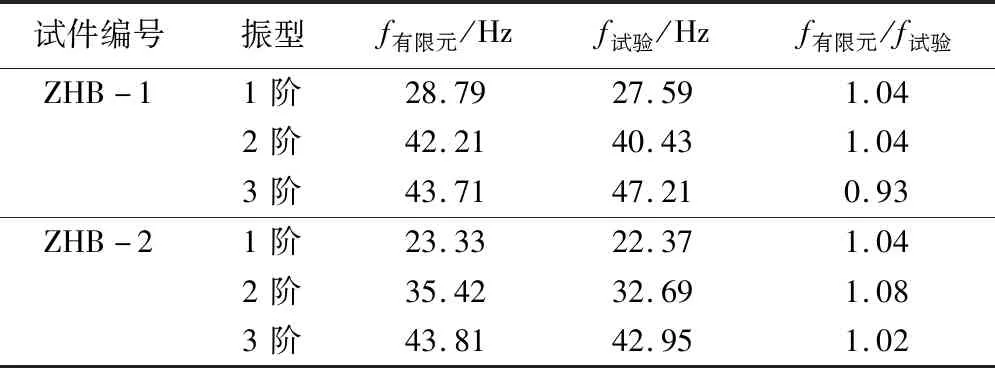
表3 试验与有限元分析不同振型自振频率

2.2.2 有限元参数分析

分析边界条件、楼盖梁间距、楼盖跨度及型钢厚度等因素对组合楼盖抗振性能的影响。以编号1、2为例，有限元模拟参数见表4。结合轻质单向板常用尺寸及稻草板实际尺寸，组合楼盖的楼盖梁选用截面尺寸A：C150 mm×50 mm×20 mm×1.5 mm，间距600 mm；B：C120 mm×40 mm×15 mm×1.5 mm,间距400 mm。边界条件为两边支撑、梁端简支。

表4 有限元模拟参数

注：FL为楼盖代号；A、B分别为截面尺寸；S为楼盖梁间距变量；K为楼盖梁跨度变量；W为楼盖宽度变量。

不同楼盖梁间距:在ZHB-1、ZHB-2有限元模型的基础上，组合楼盖的尺寸、稻草覆面板厚度及边界条件不变情况下，分析楼盖梁的间距对组合楼盖的舒适度性能的影响。不同楼盖梁间距下组合楼盖跨中挠度与自振频率分析结果见图6。

从图6中可以看出，楼盖梁间距由200 mm增大至800 mm，楼盖跨中挠度从0.484 mm增大到1.044 mm，满足组合楼盖跨中挠度规范要求。当楼盖梁截面尺寸减小时，跨中挠度和自振频率增长率变化都不大。但截面尺寸较小或楼盖梁间距过大时，自振频率不满足组合楼盖自振频率规范要求。因此，建议截面的选用不宜小于120 mm，楼盖梁间距应控制在400～600 mm。

不同楼盖跨度：在ZHB-1、ZHB-2有限元模型的基础上，其他参数不变，分析不同楼盖跨度对组合楼盖的舒适度性能的影响。不同楼盖跨度的组合楼盖跨中挠度值与自振频率见图7。

从图7可以看出，组合楼盖跨度由2 400 mm增大至3 300 mm时，刚度随之减小，使其跨中挠度增加，自振频率减小。说明适当减小组合楼盖跨度能有效地降低组合楼盖跨中挠度，提高自振频率。为尽可能满足组合楼盖的舒适度性能，建议将跨度控制在3 000 mm以内。

不同楼盖宽度：在ZHB-1、ZHB-2有限元模型的基础上，其他参数不变，分析不同楼盖宽度对组合楼盖的舒适度性能的影响。不同宽度下组合楼盖跨中挠度与自振频率见图8。

从图8中可以看出，随着组合楼盖宽度的增加，其跨中挠度呈波动性变化，是由于当组合楼盖跨中无楼盖梁时，稻草板弹性模量较小，自身在静力荷载作用下也发生变形，此时跨中挠度略大；组合楼盖自振频率随其宽度的增加而减小，但减小趋势逐渐变缓，整体变化较小。因此，组合楼盖宽度的改变对其跨中挠度与自振频率影响不大。

边界条件的影响：在ZHB-1、ZHB-2有限元模型的基础上，其他条件均不变，分析改变边界条件对组合楼盖的舒适度性能的影响。不同边界条件下组合楼盖跨中挠度与自振频率分析结果见表5。

表5 不同边界条件下组合楼盖跨中挠度与自振频率

由表2、表3和表5可知，在两边支撑的条件下，梁端固结的跨中挠度比梁端简支的跨中挠度降低了约6%，自振频率提高了约8.8%；在梁端简支的条件下，四边支撑的跨中挠度比两边支撑的跨中挠度降低了约11.3%，自振频率提高了约5.8%；四边支撑梁端固结的跨中挠度比两边支撑梁端简支的跨中挠度降低了约14.5%，自振频率提高了约11.8%。故在工程中增加楼盖梁的约束能力，能适当降低组合楼盖的跨中挠度，增加组合楼盖的自振频率，提高组合楼盖的舒适性。

2.3 公式修正

1 kN静力荷载作用于楼盖跨中时挠度按前文瑞典与澳大利亚准则进行计算，计算结果见表6。

表6 各国设计方法计算挠度与试验值

注：δS为试验挠度；δSw为根据瑞典Ohlsson准则计算的挠度；δAu为根据澳大利亚准则计算的挠度。

从表6可以看出，澳大利亚准则计算结果与试验结果相差较小；瑞典准则计算结果与试验结果相差较大。覆面板对楼盖跨中挠度有一定的影响，不能忽略覆面板对组合楼盖刚度的贡献。

针对稻草板的特殊性对澳大利亚准则进行修正，具体公式如下：

(5)

式中:α为稻草板对跨中挠度影响系数；Pd为有效荷载(Pd=kdP)，kN；L为楼盖梁跨度，mm；E为楼盖梁弹性模量，N·mm-2；Ix为单根楼盖梁惯性矩，mm4。

通过澳大利亚准则公式(2)对组合楼盖FL-1～FL-8跨中挠度进行计算，计算结果见表7。

通过origin软件对理论计算结果与有限元分析结果进行线形拟合，拟合曲线见图9。

表7 跨中挠度理论计算结果与有限元分析结果

注：δF为有限元分析挠度。

将有限元分析结果δF与澳大利亚理论计算结果δAu若干点进行拟合得到修正系数α=0.848，文中取0.8。修正后的公式如下：

(6)

采用公式(6)计算结果与试验结果比较(表8)。从表8中可以看出，理论计算与试验值误差在5%以内，与试验结果吻合良好，可采用此公式计算该组合楼盖的静力挠度。

表8 跨中挠度理论计算结果与试验结果

注：δT为根据修正后的公式(6)计算的挠度。

楼盖的自振频率按前文瑞典Ohlsson准则与美国Johnson准则进行计算，计算结果见表9。

表9 各国设计方法计算自振频率与试验值

注：fS为试验频率；fSw为根据瑞典Ohlsson准则计算的频率；fAm为根据美国Johnson准则计算的频率。

由表9可知，瑞典准则计算结果与试验结果相差较大，美国准则计算结果与试验较接近，但该准则仅适用于未居住的楼面系统人行走时引起的振动是否满足要求。对此，假定弹性变形阶段组合楼盖跨中挠度与所受的集中力成正比，结合公式(6)提出该组合楼盖自振频率的计算方法如下：

(7)

式中:f为楼盖自振频率，Hz；P为集中力荷载，1 kN；δ为楼盖跨中挠度，mm，计算方法见式(6)；m为楼盖质量，kg。

对不同工况下的2块组合楼板利用式(7)计算自振频率，与试验结果和有限元分析结果进行对比，见表10。理论计算结果与试验结果吻合良好，可采用公式(7)来计算组合楼盖的自振频率。

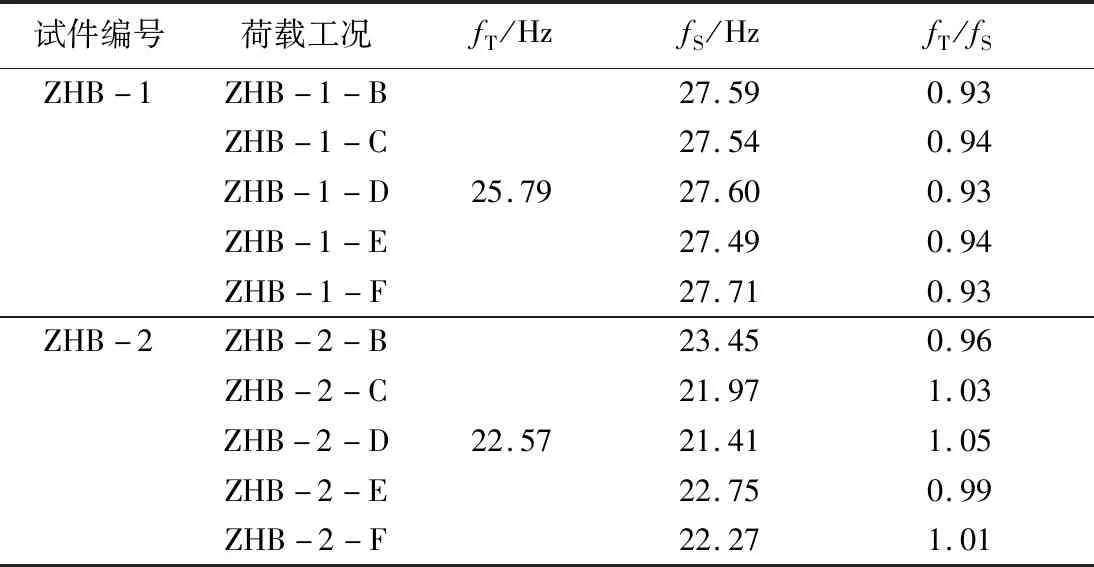
表10 自振频率理论计算结果与试验结果

注：fT为根据修正后的公式(7)计算的频率。

3 结束语

等用钢量条件下改变梁截面尺寸与梁间距可很好的控制楼盖厚度，且静力挠度改变不大，建议组合楼盖在1 kN集中荷载作用下跨中挠度限值设为2.0 mm。

等用钢量条件下增大梁的截面尺寸可以增大楼盖自振频率，考虑经济性可以通过此方法改善楼盖舒适性，且试件的自振频率均大于15 Hz。因此，建议对抗振舒适度要求较高的该组合楼盖的自振频率限值设为15 Hz。

通过有限元模型的参数分析可知，减小组合楼盖跨度、楼盖梁间距及增加楼盖边界约束能有效地降低组合楼盖跨中挠度，提高自振频率，从而提高其舒适度。

按瑞典Ohlsson准则计算组合楼盖挠度与试验结果相差较大，表明覆面板对组合楼盖整体静力挠度与自振频率影响较大，不能仅通过单根楼盖梁的惯性矩来计算挠度，需要考虑覆面板的作用。

针对稻草板修正了组合楼盖静力挠度计算公式，并提出了自振频率计算简化公式，计算结果与试验和有限元分析结果误差均小于10%，可用于估算同类楼盖自振频率。