罗田垂枝杉单木生长规律及其生物量测定1)
许业洲 吴楚 杜超群
(湖北省林业科学研究院,武汉,430079) (长江大学) (湖北省林业科学研究院)
杉木(Cunninghamialanceolata(Lamb.) Hook.)为我国特有用材树种,有一千余年的栽培历史,在多种复杂的生态环境和人为因素的作用下,杉木形成了适应各种生态环境的变异种群[1]。罗田垂枝杉(Cunninghamialanceolatavar. Luotian)是20世纪70年代中期,在湖北省罗田县发现的变异类型,与普通杉木相比有着十分显著的形态变异特征,其主干通直圆满,树冠窄小呈尖圆锥形,冠幅1.5 m左右,冠高1~2 m,侧枝自然下垂,树冠下层侧枝着生角度达150°左右,6~7年生侧枝自然枯死并从其主干着生处折断脱落,主干无侧枝节痕,出材率高[2]。罗田垂枝杉独特的树冠特征是林木理想的株型[3],这种株型能有效利用空间资源和养分,与邻近树冠干扰较少,特别适宜密植,可获得较大的单位面积产量,还可培育高品质无节装饰材,具有较高经济利用价值和较大的推广应用前景。
鄂皖交界的大别山区部分丘陵山地为杉木适宜生长区域[4],罗田垂枝杉自然分布主要集中在湖北省罗田县大崎乡毛田村,由于大面积砍伐,目前仅存3~5片面积为0.667~3.330 hm2的人工林。自发现以来,先后对其形态特征开展了调查研究,包括枝条大小、树冠形状[2]、木材物理力学性质[5]、过氧化物同工酶[6]等,并对其侧枝脱落进行了解剖学观测和生物学特性研究[7-8],并于2015年选育出植物新品种“鄂杉1号”。
建立单木生长模型是描述单株立木生长过程及其规律的主要方法和手段[9],林木生物量模型反映林分内树木的各组分干物质质量与树木其他测树因子之间的内在关系,利用生物量模型进行模拟估算是林木生物量测定的常用方法之一。杉木生长模型及生物量模型方面已有大量的研究成果,针对不同变异类型的杉木生长规律及生物量模型研究也有相关报道。贾晨等[10]采用树干解析法研究了德昌杉(Cunninghamiaunica)的生长规律并将其分为幼树期、速生期、近成熟期和成熟期4个阶段;张璐颖等[11]通过样地调查和树干解析探讨了峦大杉(CunninghamiakonishiiHayata)生长规律并拟合树高、胸径、材积生长过程;高楠[12]分析比较发现峦大杉和杉木单株各器官生物量差异极显著或显著,并初步揭示峦大杉生物量的分布规律。这些研究结果对德昌杉和栾大杉的利用起到了一定的指导作用。
罗田垂枝杉生长模型和生物量方程的研究目前还处于空白,本研究以罗田垂枝杉人工林为对象,利用树干解析数据构建单木胸径、树高、单株材积生长模型以及地上总生物量和树干、树冠、枝叶生物量模型,并分析各生长因子的变化规律,以期对这一杉木变异类型的生长过程和生物量结构进行描述与评价,为其生产应用提供理论支撑。另外,侧枝弱小和下垂是罗田垂枝杉的显著变异特征,同时构建其侧枝基径、枝长生长模型及着枝角度变化模型,以更直观和系统地揭示罗田垂枝杉形态特征的变异规律。
1 研究区概况
研究区位于湖北省东北部的罗田县(E115°6′~115°46′,N30°35′~31°16′),位于大别山南麓,东邻英山,南连浠水,西与团风、麻城接壤,北与安徽省金寨县交界。属北亚热带季风气候,冬干夏湿,春暖秋凉,年均日照时间2 047 h,年均辐射热量457.40 kJ/cm2。年平均气温16.4 ℃,极端最高气温41.6 ℃,极端最低气温-14.6 ℃,无霜期240 d。全县年均降水量1 330 mm。本研究试验样地设置点位于大别山主峰西南的鄂皖交界处,最高点海拔1 408.2 m,系长江、淮河的主要分水岭之一,常年降水量为1 450 mm,平均气温16.4 ℃。
2 研究方法
2.1 数据来源
在研究区内选择保存较完整、具代表性的垂枝杉人工林,设置面积120~200 m2的样地,样地内每木检尺,调查记录胸径、树高、活枝高、冠幅等测树因子。在样地内根据平均胸径和树高选取1株平均木作为样木,将样木伐倒后,采用分层切割法,将树冠按80 cm长度分层,每一冠层内选取3~5个标准枝作为样枝测定枝长、基径及着枝角度等,通过枝解析,确定样枝枝条年龄。分层称取各层全部活枝鲜质量及样枝的枝叶鲜质量,105 ℃恒温干燥后称量干质量,计算样枝的枝生物量及叶生物量,换算成树冠总生物量。将样木按2 m区分段进行树干解析,分别截取树干基部、各区分段中央、梢底圆盘并称取鲜质量及干质量,换算树干干质量及样木树干生物量。共取得26株样木各调查因子及解析资料(见表1)。

表1 样木调查统计表
2.2 生长量模型
选择逻辑斯蒂(Logistic)、考尔夫(Korf)、坎派兹(Gompertz)、理查德(Richards)、广义单分子型(Mitscherlich)方程为单木各生长因子随年龄变化曲线的候选方程[13]。各方程表达式如下:y=a/(1+b×e-cA)(逻辑斯蒂模型);y=a·e-b·A-c(考尔夫模型);y=a·e-b·e-c·A(坎派兹模型);y=a·(1-e-b·A)c(理查德模型);y=a+b·e-c·A(广义单分子型模型)。式中,A为树木或枝条年龄;y调查因子的值(包括立木胸径、树高、单株材积和枝条基径、枝长、着枝角度;a为各因子最大值参数;b为与初始值有关的参数;c为最大生长速率参数。
2.3 单株材积和生物量估算模型
单株材积和生物量采用线性模型、一元方程和二元方程估算。方程具体表达式如下:Y=a+b·D(线性模型);Y=a·Db(一元方程);Y=a·Db·Hc(二元方程)。式中:Y为单株材积或生物量(地上部分总生物量、树干生物量、树冠生物量、枝生物量、叶生物量);D、H分别胸径和树高;a、b、c为参数。
2.4 模型精度检验
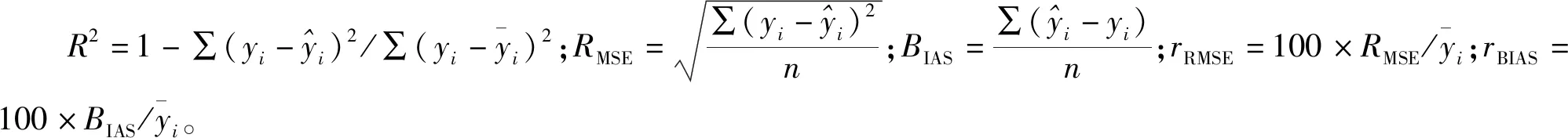
3 结果与分析
3.1 单木生长模型及其规律
由表2可知,从各统计参数看,胸径、树高和单株材积各方程的拟合效果比较相近。但考尔夫模型拟合的3个方程的a值均偏大且超出杉木正常生长范围,广义单分子型模型在胸径、树高方程中的b值和材积方程中的a值均出现异常,而理查德模型在单木材积模型中的参数a值也有悖于其真实生长量,其他各方程参数t检验均达到极显著水平(P<0.01)。从以上两个方面考虑,选择理查德模型为罗田垂枝杉单木胸径和树高生长方程,坎派兹模型为单株材积生长方程,所选模型在各类生长方程中的估计偏差及其比例均为最小,拟合精度最高。

表2 单木胸径、树高、材积生长模型拟合参数与统计指标
注:表中** 、*分别表示在0.01和0.05水平上显著。
由图1可知,罗田垂枝杉胸径、树高总生长量曲线近似为“S”型;材积总生长量曲线呈“J”型,由于样木多为中龄林,单株材积处于增长期而未达到最大值。
胸径生长量在5~7 a进入速生期,年均生长量达到0.50 cm;8~11 a为快速生长期,胸径连年生长量达到最大值为0.75 cm;14~17 a时,胸径平均生长量达到0.62 cm,随后平均生长量曲线和连年生长量曲线在18~19 a出现交点,胸径生长量增速放缓,但幅度较小;20 a后连年生长量降至0.50 cm以下,而平均生长量保持在0.60 cm,与快速生长期的生长速度相当。
树高在幼龄期生长最快,3~6 a时,连年生长量最大达到0.75 m;5~10 a时,平均生长量最大(0.70 m),平均生长量曲线和连年生长量曲线在7 a左右出现交点,随后树高平均生长量以每年2%左右的幅度缓慢下降,而连年生长量的每年下降幅度为3%~5%。
单株材积生长过程有别于胸径与树高,前10 a材积增长较慢,12 a后生长逐渐加快,25 a时材积总生长量、连年生长量和平均生长量分别为0.131 0 m3、0.011 7 m3和0.005 2 m3,均未达到最大值,材积平均生长和连年生长曲线未出现交点,且平均生长量一直低于连年生长量,也未出现明显下降趋势,材积生长处于旺盛期。
3.2 侧枝生长及着枝角度变化规律
由表3可知,侧枝基径生长模型的拟合优度为0.866 3~0.952 7,残差标准差为2.317 2~2.436 0,均方根误差在2.3左右,偏差均小于0.2,综合比较选择拟合优度最高而其它统计指数较低的理查德模型为基径最优生长模型。枝长生长模型中理查德模型、广义单分子模型和考尔夫模型的拟合优度均超过0.99,但广义单分子模型和考尔夫模型的参数a值异常,理查德模型、考尔夫模型及坎派兹模型的均方根误差和偏差分别为25.0左右和-7.0左右,因此,综合选择理查德模型为最优枝长生长模型。着枝角度模型拟合优度在0.74左右,残差标准差12.5左右,除坎派兹模型和广义单分子型模型外,其它模型的统计参数较低且相近,因此,综合选择逻辑斯蒂模型为着枝角度模型。

表3 侧枝生长及着枝角度模型拟合参数与统计指标
由图2a可以看出,侧枝基径1年生时生长量最大(0.95 cm),2~4 a生长量逐年减缓,其平均生长量从0.64 cm降低到0.39 cm,连年生长量从0.32 cm下降至0.10 cm,第5年连年生长量基本接近0。图2b中侧枝枝长1~3 a为速生期,3年生平均生长量和连年生长量均达到最大值,第4年开始缓慢下降,第6年连年生长量仅为8.4 cm。图2c中着枝角度变化曲线与图2a中基径生长曲线相似,但变化趋势略平缓,着枝角度在第1~3 a增幅较大,年均增幅超过35.5°,但增幅逐年减小,4~6 a的年均增幅在25°左右,而6年生侧枝着枝角度连年增幅仅为4°。
3.3 单株材积预估模型
由表4可知,各方程的拟合优度均在0.93以上,二元方程拟合优度更高,比线性方程提高5.6%,而且各方程统计参数均为二元方程最小(绝对值),其中残差标准差、均方根误差和平均残差分别比线性方程降低44.8%、44.7%和88.5%,说明二元方程能较好地拟合材积生长量并对其进行较为准确的预估。

表4 材积方程拟合参数与统计指标
3.4 生物量预估模型
由表5可知,各生物量线性方程和一元方程拟合优度及各统计参数相差不大,其中地上部分总生物量和树干生物量与胸径呈较强相关关系,拟合优度约0.87,枝生物量与胸径呈中度相关,拟合优度0.52~0.55,而树冠和叶生物量与胸径相关性较弱,拟合优度0.4以下;增加树高指标后的二元方程均能提高模型拟合优度并降低残差标准差、均方根误差等统计参数,其中地上部分总生物量和树干生物量的拟合优度提高6%,残差标准差降低20%,但对其它生物量模型影响不大。利用胸径、树高生长量或仅用胸径生长量均可对罗田垂枝杉地上部分总生物量和树干生物量进行较为准确的预估,但对枝、叶及树冠生物量的预估精度较差。

表5 生物量拟合参数与统计指标
由图3可知,地上部分总生物量和干生物量均随胸径增大而明显增大,最大胸径生物量分别是最小胸径生物量的3.1倍和3.5倍,两者增加趋势和增幅几乎一致,呈平行关系。冠生物量及枝、叶生物量变动幅度较小,单株变异系数均小于30%,随胸径呈弱的增大趋势,证明了仅用胸径生长量预估其树冠生物量存在较大误差。
4 结论与讨论
在不考虑竞争关系的杉木单木生长模型中,理查德理论方程具有广泛的适用性和较好的拟合效果[15]。本研究中罗田垂枝杉胸径、树高生长方程均以理查德模型最优,拟合优度均在0.88以上,而材积生长方程以坎派兹模型最优。利用这些方程绘制的曲线图较为客观地反映了罗田垂枝杉树高、胸径和材积的生长规律。以本地普通杉木以及福建峦大杉[11]和四川德昌杉[10]这两个杉木变异类型作为对照,罗田垂枝杉胸径、树高总生长量分别比本地杉木(胸径13.1 cm、树高12.0 m)提高了6.1%和13.1%,比福建峦大杉分别(胸径18.6 cm、树高15.5 m)降低了25.3%和12.3%,比四川德昌杉(胸径17.9 cm、树高12.9 m)的胸径降低了22.3%,树高提高了5.4%。总体而言,罗田垂枝杉、四川德昌杉的生长量均明显小于福建峦大杉,胸径、树高最大连年生长量分别为福建峦大杉的51.7%~67.6%和55.6%~57.0%,主要与不同生长区域气候特征及杉木不同类型的生长特性有关,需要在不同区域开展罗田垂枝杉的引种栽培试验以检验其适应性。
通过拟合选择理查德模型为罗田垂枝杉侧枝基径和枝长生长模型,逻辑斯蒂模型为着枝角度变化模型,对罗田垂枝杉1~6年生侧枝枝长、基径和着枝角度的模型拟合结果分别为25.89~49.79 cm、1.03~1.59 cm和64.1°~130.9°,与罗田垂枝杉树冠结构及其变异特性的研究和实际调查结果一致[16]。吴明钦[17]对福建杉木人工林树冠结构的研究表明,杉木一级侧枝枝长、基径、着枝角度分别为0.12~3.35 m、0.58~4.02 cm、10.0°~87.5°,罗田垂枝杉侧枝枝长、基径和着枝角度分别是福建杉木的44.8%、39.6%和149.6%。罗田垂枝杉的侧枝生长量明显偏小而着枝角度明显较大,树冠生长、结构及形态均具有明显的变异特征,其侧枝在2~3 a时快速生长,生长至4~5 a就基本停滞,而当年生侧枝着枝角度超过60°且逐年增大,生长4 a时达到130°左右,5~6年生侧枝基本保持这一着枝角度直至自然枯死脱落。
罗田垂枝杉单木材积与其胸径和树高均呈较强线性关系,相关系数0.87,二元材积方程拟合优度及各统计参数均优于线性和一元材积方程,与曾鸣等[18]、曾伟生等[14,19]建立模型的预估结果较一致。罗田垂枝杉单株材积理论值为0.209 m3,与行业标准《立木材积表》一般产区杉木单株材积(0.186 m3)相比提高12.3%,6~14年生罗田垂枝杉单株材积比一般杉木平均大10.2%。在杉木一般产区(湖北),罗田垂枝杉立木材积比一般杉木提高10%以上,如果充分利用其树冠窄小的变异特性,将其造林密度提高1倍,其人工林单位面积产量可显著提高。罗田垂枝杉窄小的树冠特征,与邻近树冠干扰较少,更有效利用空间,在人工纯林中能获得更大的单位面积产量。
在杉木单株或人工林生物量分配及模型估算方面,大部分研究结果表明,以胸径和树高的二元生物量模型的拟合效果较好[20-21]。本研究也得出利用二元方程对罗田垂枝杉生物量的预估效果更优的结论,但从地上部分各器官生物量来看,树干生物量拟合优度最大(0.915 2),而枝、叶生物量的拟合优度均较低(分别为0.542 7、0.324 6),与李燕等[20]、赵嘉诚等[21]对于普通杉木的研究结果相比存在较大差异,这一差异客观地反映出罗田垂枝杉(侧枝自然枯死脱落形成枝叶生物量及其变化幅度较小)树冠变异特征,其枝叶生物量(树冠生物量)仅占地上部分总生物量的11.0%,明显低于胡炎红等[22]得出的鄂西杉木枝叶占全株总生物量24.0%的结果。罗田垂枝杉树干及地上部分生物量与胸径呈较强的线性关系,但枝叶生物量及树冠生物量与胸径的线性关系较弱,与普通杉木随林木生长而明显增大的趋势不一致。由于罗田垂枝杉具有特殊的树冠变异特征,常规生物量估测方法只适于其树干或地上部分总生物量的预估,对其枝叶或树冠生物量的估测方法还有待进一步研究。

