Hermitian矩阵空间上的1蛐2-Jordan可乘保极小秩映射
郭 钰,贾艳萍
(山西大同大学数学与计算机科学学院,山西大同 037009)
Hermitian矩阵空间上的1蛐2-Jordan可乘保极小秩映射
郭 钰,贾艳萍
(山西大同大学数学与计算机科学学院,山西大同 037009)
证明了Hermitian矩阵空间上的1/2-Jordan可乘保极小秩映射是可加的而且是酉相似变换或者是转置映射复合酉相似变换。
Hermitian矩阵;1/2-Jordan可乘映射;极小秩
设R为环,对于任意的A,B∈R,定义AoB=1/2(AB+BA)。若映射φ:R→R满足φ(AoB)=φ(A)oφ(B)对所有A,B∈R都成立,则称φ为R上的1/2-Jordan可乘映射。
令C表示复数域。Mn表示n×n复矩阵代数。对于A∈Mn,rank(A)表示矩阵A的秩,mr(A)=min{rank(A-λI):λ∈C}称为A的极小秩[1-3]。记Γk={A:mr(A)=k},映射φ:Mn→Mn若满足φ(Γk)⊂Γk,k=0,1,…,n-1,则称φ为保极小秩映射,若φ为1/2-Jordan可乘映射且保极小秩,则称φ为1/2-Jordan可乘保极小秩映射。。
极小秩是建筑、工程、控制等方面重要的不变量之一[4-6]。矩阵的极小秩是与矩阵的不变因子的个数密切关联的概念。对于A∈Mn,用i(A)表示A的非平凡不变因子的个数,则有mr(A)+i(A)=n[7]。因此,保极小秩的映射同时也是保持矩阵的非平凡不变因子的映射。
Hn表示n×nHermitian矩阵空间。讨论Hn上的1/2-Jordan可乘保极小秩映射。注意到,在多数情况下,算子代数上保持算子的某种性质或算子之间的某种关系不变的可乘映射是可加的。比如,B(H)(Hilbert空间上的有界线性算子全体)上的有界保秩可乘映射是可加的[8],矩阵代数上的保秩(保谱半径或保数值域半径)可乘映射也是可加的[9],因而这种映射本质上是环同态。将证明Hn上的1/2-Jordan可乘保极小秩映射也是可加的,进而是环同态。
下面给出一些记号。对于A∈Mn,At表示A的转置矩阵。设τ为复数域C上的映射,定义Aτ=[τ(aij)]。Pn表示Hn中的幂等矩阵全体(即为投影)。和分别表示Pn中的k秩矩阵全体和Hn中的k秩矩阵全体,1≤k≤n。Eij表示第i行第j列为1,其他位置都为0的矩阵。
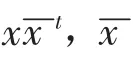
由极小秩的定义可知,对于A∈Mn,n≥2,A的极小秩具有如下性质:
(a)平移不变性:mr(A+λI)=mr(A),λ∈C;
(b)相似不变性:mr(TAT-1)=mr(A)对任意可逆的T∈Mn成立;
(c)数乘不变性:mr(λA)=mr(A),0≠λ∈C;
(d)0≤mr(A)≤n-1且mr(A)≤rank(A);
(e)rank(A)=1⇒mr(A)=1;
(f)对任意单射环同态τ:C→C有mr(Aτ)=mr(A)成立;
(g)mr(A)=0⇔A∈CI;
下面给出本文主要结论及证明。
定理1 设n≥2,1/2-Jordan可乘单射φ:Hn→Hn保极小秩,则存在酉矩阵U∈Mn使得或者φ(A)=UAU*对所有A∈Hn成立,或者φ(A)=UAtU*对所有A∈Hn成立。
证明 分几步证明。断言1 φ(I)=I,φ(0)=0。
设φ(I)=αI,φ(0)=βI,α,β∈C。对任意A∈(C),有φ(0)=φ(0oA)=φ(0)oφ(A)=βI,蕴含φ(A)=I或者β=0。显然φ(A)≠I,故φ(0)=0。对任意P∈Pn,φ(P)=φ(PoP)=φ2(P),即φ(Pn)⊂Pn。因此,α2=α。若α=0,则φ(A)=φ(AoI)=0,矛盾。故φ(I)=I。
断言2 φ在偏序集Pn上保序保正交。
若P1,P2∈Pn,P1≤P2(即P1P2=P2P1=P1),则φ(P1)=φ(P1oP2)=φ(P1)oφ(P2),即φ(P1)φ(P2)+φ(P2)φ(P1)=2φ(P1),用φ(P1)分别左乘和右乘上式,可得φ(P1)φ(P2)=φ(P2)φ(P1)=φ(P1),即φ(P1)≤φ(P2)。
若P1⊥P2,
则0=φ(P1oP2)=φ(P1)oφ(P2)。
因此φ(P1)oφ(P2)=0。用φ(P1)分别左乘和右乘上式,可得φ(P1)φ(P2)=φ(P2)φ(P1)=0,即φ(P1)⊥φ(P2)。
断言3 存在保单位元的映射τ:C→C使得φ(λA)=τ(λ)φ(A)对所有A∈Hn,λ∈C成立。
对任意λ∈C,A∈Hn,φ(λA)=φ(λIoA)=φ(λI)oφ(A)。设φ(λI)=τ(λ)I,则φ(λA)=τ(λ)φ(A)。易见,τ:C→C为保单位元的映射。
由φ(P)=φ(P2)=φ2(P),也就是(δy⊗y+ξI)2=δy⊗y+ξI,从而δ2+2ξδ=1,ξ2=ξ。所以ξ=0。此即φ把一秩幂等元映为一秩幂等元。
证明ξ=0,δ=1。若ξ=1,取秩一投影,z⊗z与x⊗x正交,则由断言2可知,φ(x⊗x)与φ(z⊗z)正交,矛盾。
断言5 若P1,P2,…,Pk是一组两两正交的一秩投影等元,记P=P1+P2+…+Pk,则φ(P)=φ(P1)+φ(P2)+…+φ(Pk),且φ(Pi)⊥φ(Pj),i≠j。
由φ的保序性可知φ(P1)+φ(P2)+…+φ(Pk)≤φ(P),且容易证明当k>n-k时,mr(P)=n-k;当k<n-k时,mr(P)=k。
当n=2时,结论显然成立。故只需考虑n≥3的情形。若k=n,由φ(I)=I,结论显然成立。以下考虑k<n的情形。又可分为三种不同情形:;。其中表示不超过的最大整数。若,则φ(P)=Q1+Q2+…+Qk,或者φ(P)=T1+T2+…+Tk+I,其中Q1,Q2,…,Qk是一组两两正交的一秩投影,-T1,-T2,…,-Tk是一组两两正交的一秩投影。记-(T1+T2+Λ+Tk)=D,则I-D为k个一秩投影的和。另一方面,φ(P1)+φ(P2)+…+φ(Pk)≤φ(P),从而φ(P)=φ(P1)+φ(P2)+…+φ(Pk)。
则mr(P)=n-k,
由 φ(P1)+φ(P2)+…+φ(Pk)≤φ(P)
可知,只能φ(P)=φ(P1)+φ(P2)+…+φ(Pk)。
φ(P)=φ(P1)+φ(P2)+…+φ(Pk)+Sk+1+…+Sn-k,
则 φ(P)φ(I-P)=(φ(P1)+φ(P2)+…+φ(Pk)+Sk+1+…+Sn-k)(Q1+Q2+…+Qn-k)≠0,矛盾。
断言6 若P1,P2,…,Pk是一组两两正交的一秩投影,0≠λi∈F,1≤i≤k,则
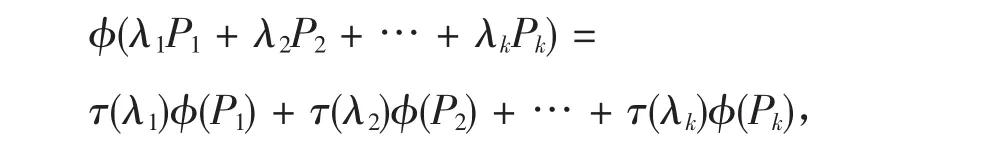
其中φ(Pi)⊥φ(Pj),i≠j。
容易证明
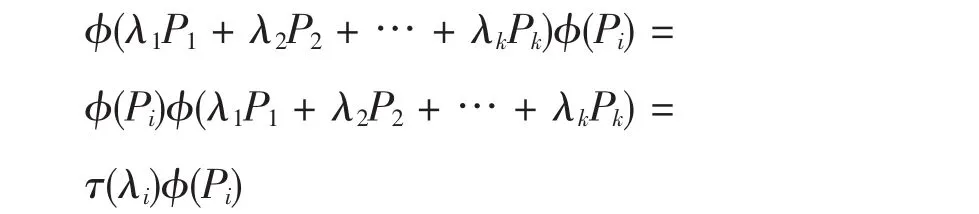
1≤i≤k。另一方面,由于
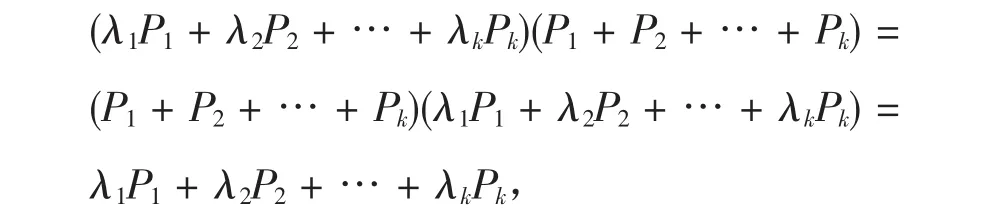
从而
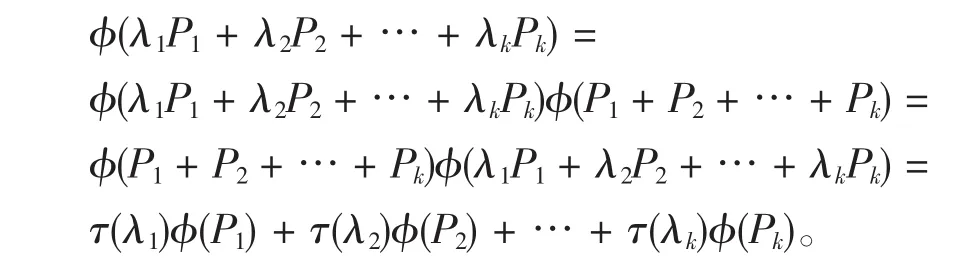
断言7 φ可加。
由谱分解定理可知,任意A∈Hn,存在λi∈C以及一组相互正交的一秩投影Pi,1≤i≤k,使得A=λ1P1+λ2P2+…+λkPk,由断言6可知φ保秩。另外,注意到φ是单射,从而由文献[11]可知φ可加。
由文献[10]可知,φ可加保秩当且仅当φ为以下形式之一:
1)φ(A)=εUAU*对所有A∈Hn成立,其中ε∈{-1,1},U∈Mn可逆;
2)φ(A)=εUAtU*对所有A∈Hn成立,其中ε∈{-1,1},U∈Mn可逆;
因为φ保极小秩,所以ε=1。另外,由φ为1蛐2-Jordan可乘映射可知U*U=I,即U为酉矩阵,证毕。
注 由定理1可知1蛐2-Jordan可乘保极小秩映射是保秩的。
对于实对称矩阵空间的情形,以下结论显然。我们用Sn表示n×n实对称矩阵空间,Mn(R)表示n×n实矩阵代数。
推论1 设n≥2,1蛐2-Jordan可乘单射φ:Sn→Sn保极小秩,则存在正交矩阵T∈Mn使得或者φ(A)=TAT-1对所有A∈Sn成立,或者φ(A)=TAtT-1对所有A∈Sn成立。
[1]Guo Y,Hou J C.Minimal rank perserving additive mappings on upper triangular matrices[J].Journal of Mathematical Research& Exposition,2011,31(6);951-964.
[2]Zhang X L,Cui Y H,Hou J C.Jordan semi-triple mappings preserving rank andminimal rank[C].Proceedings of The Third International Workshop on Matrix Analysis,2009:273-276.
[3]W So.Linear operators perserving theminimal rank[J].Linear Algebra Appl,1999(302):461-468.
[4]Yang Q,Liu J.Structural damage detection withminimal update method[J].Journal of Vbtation and Shock(Shanghai),2008,27(4):7-9.
[5]Zhu Z,Cao S.Damage identification of truss structures using aminimum rank method[J].Journal of Hebei Institute of Architec tural Science and Technology,2006,23(3):7-10.
[6]孟丽娜,田国华.关于矩阵空间上的保极小秩问题的研究[J].黑龙江工程学院学报,2007,21(4):74-76.
[7]Oliveira G N,Sá E M,Silva J A D da.On the eigenvalues of the matrix A+XBX-1[J].Lin Multilin Alg,.1997(5):119-128.[8]Molnár L.Some multiplicative preservers on B(H)[J].Lin Alg Appl.1999,301:1-13.
[9]安桂梅,侯晋川.矩阵代数上的可乘保秩映射[J].数学物理学报,2008,28A(6):1194-1205.
[10]Xiang-Yu Gao,Xian Zhang.Additive rank-1 preservers between spaces of Hermitian matrices[J].J Appl Math Comput,2008,26:183-199.
[11]An R L,Hou J C.Additivity of Jcrdan multipliective mcps on Jcrdan operator algebras[J].Taiwanese J Math,2006,10(1):45-46.
〔责任编辑 高海〕
Minimal Rank Preserving 1/2-Jordan Maps on the Space of Hermitian Matrices
GUO Yu,JIA Yan-ping
(School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009)
In this paper,we show that the 1蛐2-Jordan maps that preserve the rank on the space of Hermitian matrices are additive,and moreover they are unitary similarity transformations or unitary similarity transformations compound with transpose.
1蛐2-Jordan map;minimal rank;Hermitian matrix
O177.1
A
1674-0874(2012)05-0001-03
2012-05-25
国家自然科学基金项目[11171249];山西大同大学博士科研启动经费资助[2011-B-01]
郭钰(1983-),男,山西偏关人,博士,讲师,研究方向:算子代数与算子理论量子信息理论。

