一维非齐次波动方程的求解方法

张子珍，林 海

（山西大同大学物理与电子科学学院，山西大同 037009）

一维非齐次波动方程的求解方法

张子珍，林 海

（山西大同大学物理与电子科学学院，山西大同 037009）

非齐次偏微分方程是数学物理方程教学中的难点，本文以一维非齐次波动方程为例，提出各种不同的解法，以便对教学起到促进作用。

偏微分方程；分离变量法；冲量法；拉普拉斯变换法；付立叶变换法；格林函数法

在偏微分方程的教学中，非齐次方程的求解是教学中的难点，尤其是边界条件不同，如混合问题或哥西问题［1］处理方法则灵活多样，这给学生造成一定的困难。为此，本文对一维非齐次方程的求解方法进行归类，以便对该问题有一个总体的认识。

1 混合问题的求解

混合问题，是指既有初始条件又有边界条件。现以非齐次波动方程为例，来讨论混合问题的求解方法。假设边界条件是齐次的，因为如果边界条件是非齐次的，可以先将边界条件齐次化后，再进行求解。

1.1 分离变量法

分离变量法的基本思想是，令u（x，t）＝X（x）T（x），将一个偏微分方程化为两个常微分方程，其中的一个常微分方程可以构成本征值问题，从而求出本征值和本征函数，然后代入另一个常微分方程去求解。以下面的方程为例加以说明。

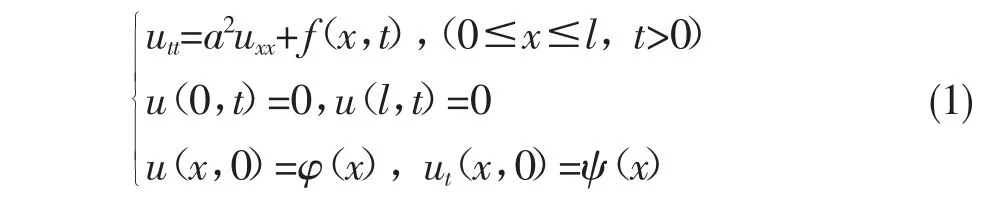
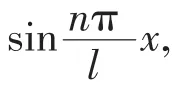
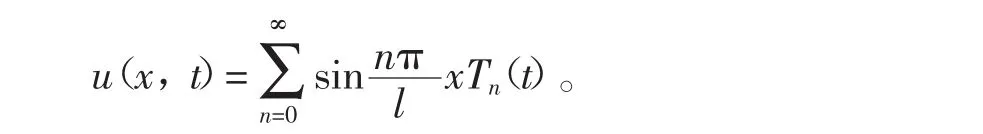
同时将f（x，t）按本征函数展开，代入方程中得：

代入初始条件，可求得系数，

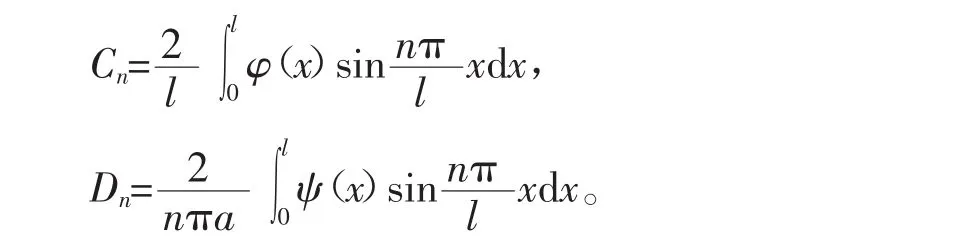
1.2 冲量法［2］

应用冲量法的前提是初始条件均取零值。仍以两端固定的弦振动为例，利用线性方程的叠加原理，方程（1）可分解为

u（x，t）＝uⅠ（x，t）+uⅡ（x，t）。

城市平均投资回报率是指投资到除港口外的其他产业平均得到的收益，先把城市内上市公司作为样本，筛选出对经济有贡献的指标(如：应付职工薪酬、固定资产折旧额、营业利润和税收等)，得到其经济的贡献量，再计算其资产总额的贡献率。

令uⅠ和uⅡ分别满足

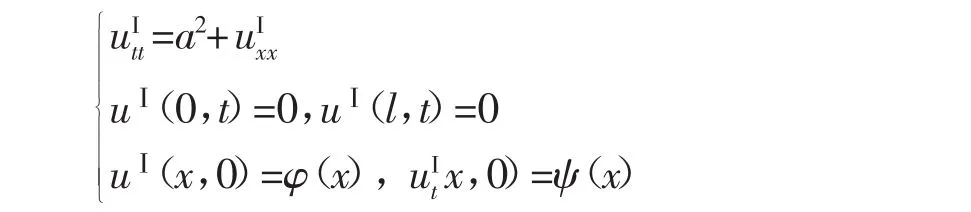
和

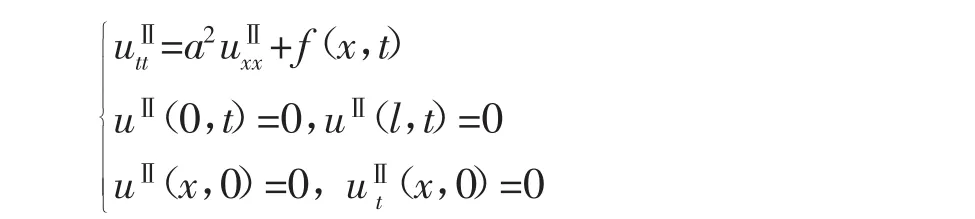
这样，方程（1）的解可转化为求解uⅠ和uⅡ。uⅠ是齐次方程齐次边界条件，它的解是

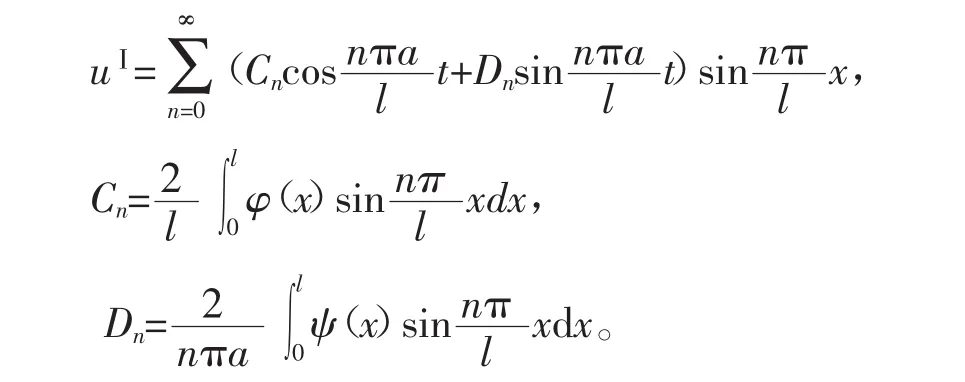
uⅡ是非齐次方程，但初始条件已化为零，可以用冲量法来求解。

冲量法的基本思想是，将持续作用的力看作是许许多多前后相继的瞬时力，持续作用力引起的振动看作所有瞬时力引起的振动的叠加，即

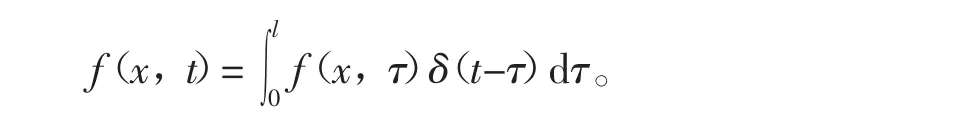
（fx，τ）δ（t-τ）可看作是作用在τ时刻的瞬时力，把该瞬时力引起的振动记为ν（x，t，τ），则ν（x，t，τ）满足定解问题

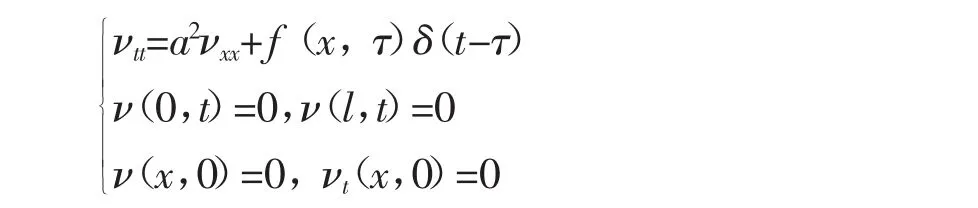
f（x，τ）δ（t-τ）这个力只作用在τ时刻，在τ-0它尚未起作用，弦仍是静止的，它的速度也为0，到τ+0时刻，这个力已作用结束，时间非常短，故弦上各点位移根本来不及变化，变化的只是速度，相当于将ν的方程两边对t进行积分得

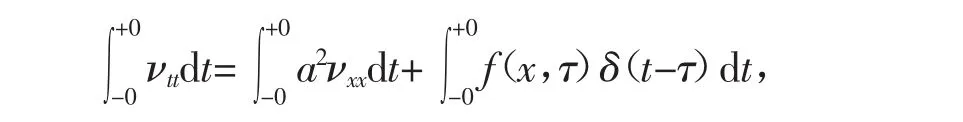
νt|τ+0＝（fx，τ）。如果取τ+0作为初始时刻，由于该瞬时力已经作用过了，弦上不受外力，故ν（x，t，τ）满足的方程应为齐次方程，其定解问题为

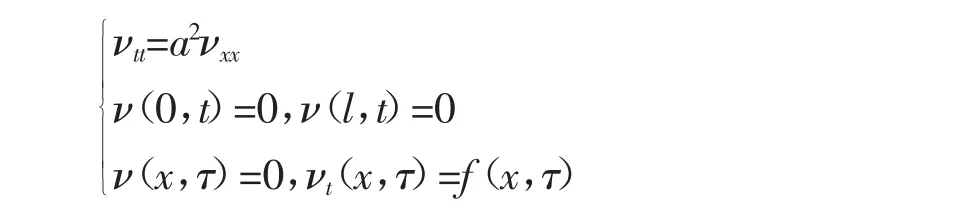
这是齐次方程齐次边界条件，只是计时起点变成了τ，所以只要将其解中的t换成t-τ就可以了。

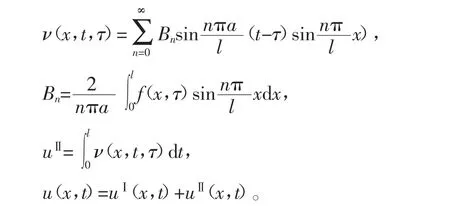
1.3 拉普拉斯变换法

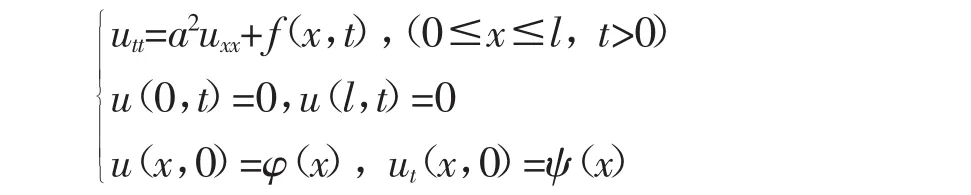
方程及其边界条件两边对变量t进行拉氏变换得

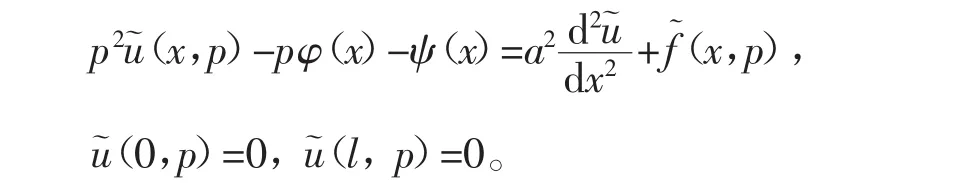
求解得：

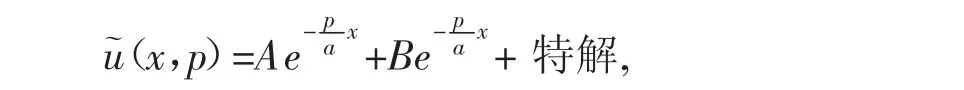
通过边界条件求出系数A和B，再通过逆变换解出u（x，t）。

2 哥西问题的求解

哥西问题，是指两端无界，即-∞＜x＜∞，因为没有边界条件的限制，所以不能构成本征值问题。哥西问题可用付立叶变换法和格林函数法求解。

2.1 付立叶变换法［3］

付立叶变换法（简称付氏变换）的思想是通过积分，如

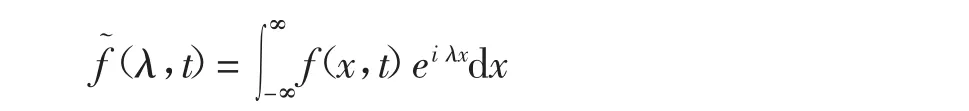
使原变量x变成新变量λ，而且通过变换原来的偏微分方程可变为常微分方程，从而使求解变得相当简单，仍以一维波动方程为例进行求解。

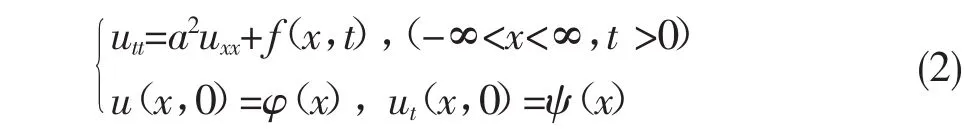
利用线性方程的叠加原理，方程（2）可分解为

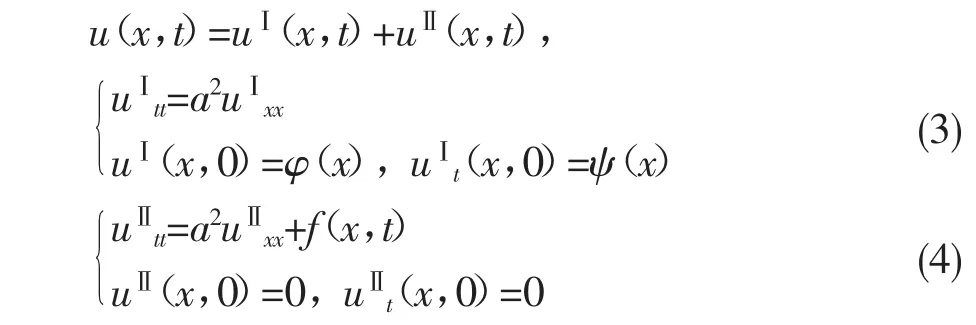
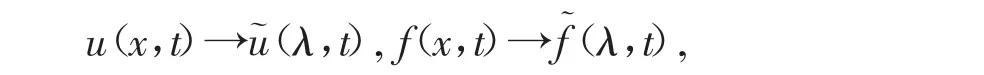
则定解问题（3）变成

解uⅡ时仍用冲量法，使

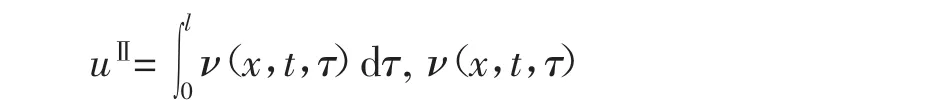
满足的方程应为齐次方程，其定解问题为

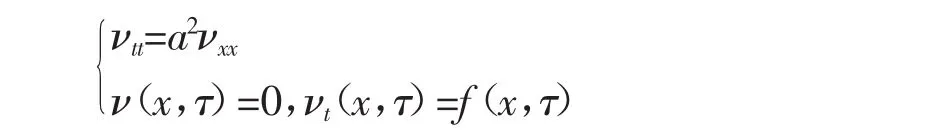
对以上方程再应用付氏变换法，求得

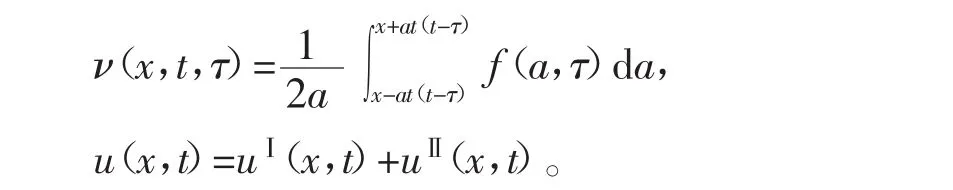
2.2 格林函数法

由于线性方程满足叠加性，格林函数法的思想是，先求出点源的解，把任意源看作是点源的叠加，任意源引起的振动看作是点源引起的振动的叠加。仍以一维波动方程为例，进行求解。

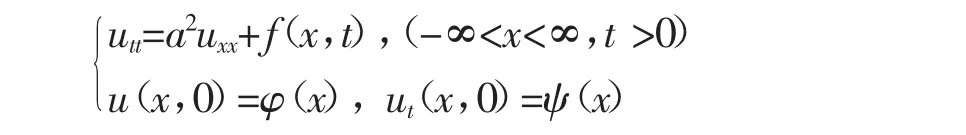
u对应的格林函数满足的方程为

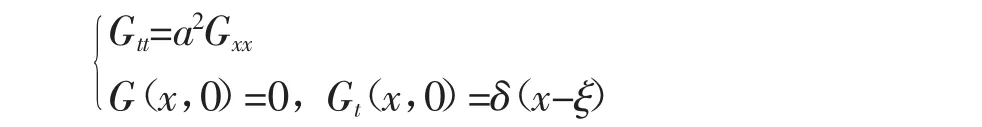
用付氏变换法求得G的像为

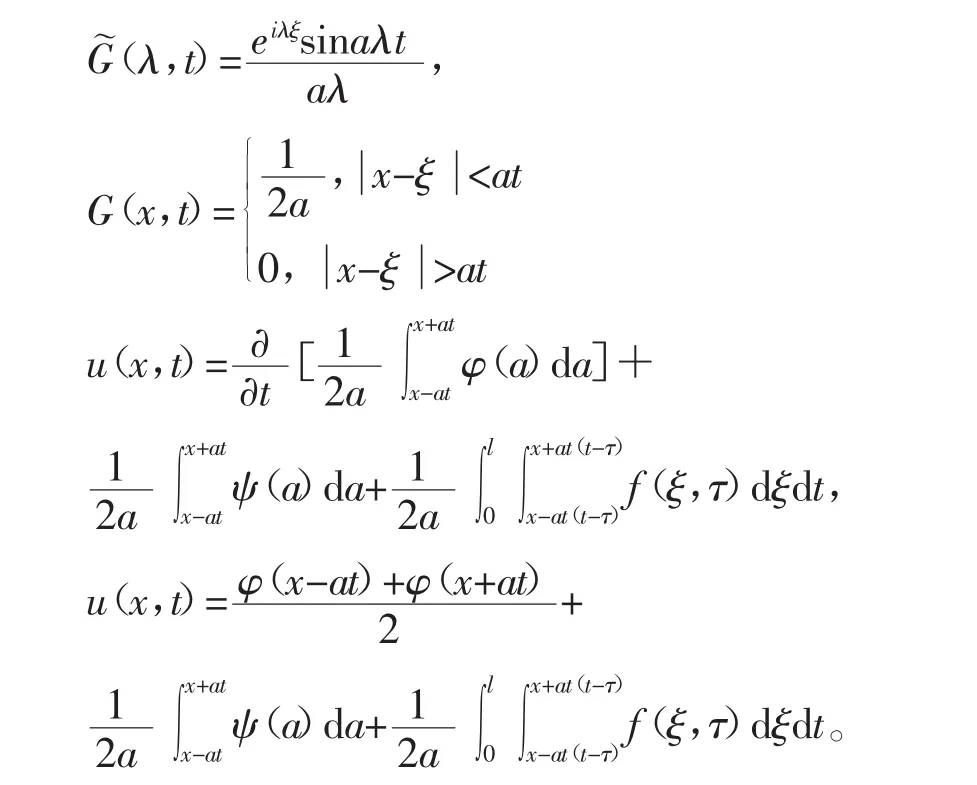
3 总结

从以上的分析可见，偏微分方程的求解方法多种多样，应根据不同的类型，不同的边界选取不同的方法。有时，同一个定解问题有多种不同的方法，应从中选取最简单而有效的方法去求解。

［1］四川大学数学系.高等数学第四册（数学物理方法）［M］.北京：高等教育出版社，2005：147-150.

［2］梁昆淼.数学物理方法［M］.北京：高等教育出版社，2000：206-210.

［3］陈义成.数学物理方法难点浅析［J］.高等函授学报，1994（5）：5-10.

〔责任编辑 李海〕

The Methods of Solving One Dimension Non-Homogeneous Wave Equation

ZHANG Zi-zhen，LIN Hai
（School of Physical Science and Electronics，Shanxi Datong University，Datong Shanxi，037009）

It is very difficult solving Non-homogeneous partial differential equation.We take up various methods of solving Non-homogeneous Wave Equation so that we promote teaching and learning.

partial differential equation；separation of variable；theorem of impulse；Laplace transform；Fourier transform；Creen function

O411.1

A

1674-0874（2012）05-0026-03

2012-08-06

张子珍（1965-），女，山西阳高人，硕士，教授，研究方向：理论物理。