具强阻尼项波动方程的整体解的渐近性

陈金梅，王祥，赵嬛嬛，刘有军

（1.忻州师范学院数学系，山西忻州 034000；2.山西大同大学数学与计算机科学学院，山西大同 037009）

具强阻尼项波动方程的整体解的渐近性

陈金梅1，王祥1，赵嬛嬛2，刘有军2

（1.忻州师范学院数学系，山西忻州 034000；2.山西大同大学数学与计算机科学学院，山西大同 037009）

在考虑强阻尼效应的情形下，研究了一类轴向载荷作用下的弹性波动方程的扰动问题的整体解的性态。以Sobolev空间的性质为工具，利用Gronwall不等式及数学归纳法，证明了该扰动问题在线性边界条件下弱解的存在唯一性。

非线性；梁方程；扰动问题；整体解

非线性发展方程是许多非线性问题在数学中的表现。自80年代初开始，对非线性发展方程的经典解的整体存在性的研究提出了一套新的处理方法，就是对解的能量估计的基础上，再利用相应的线性齐次方程的解在t→+∞时的衰减性质，并将两者有机地结合起来，就可以在一定条件下对小初值的情形得到经典解的整体存在性。

我们考虑以下的扰动问题（Pε），其中ε是一个小参数，并且|ε|≤1：

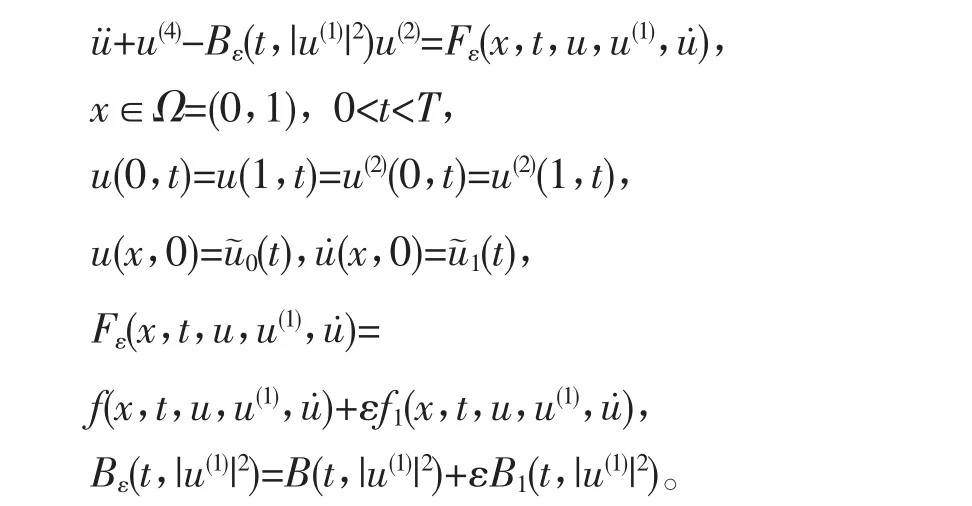
其中B，B1，f，f1是给定的函数，B（t，|u（1）|2）是轴向载荷作用，f（x，t，u，u（1），）为强阻尼效应。

B（t，|u（1）|2）与f（x，t，u，u（1），）依赖于积分：

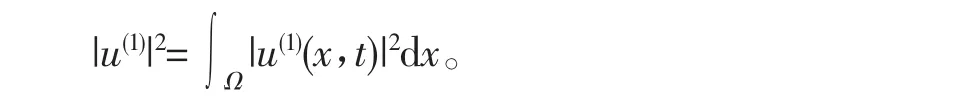
1 预备知识

记Ω＝（0，1），Q＝Ω×（0，T）

Lp＝Lp（0，1），Hm＝Hm（0，1），（0，1）。L2中的范数用|.|表示，L2中的内积用＜·，·＞表示。

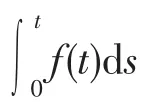
此外，定义：

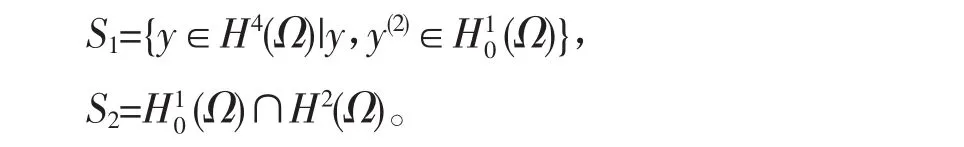
2 主要结果及其证明

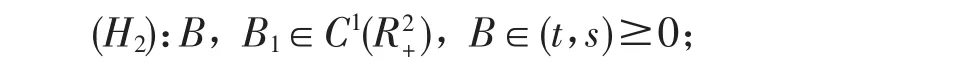
（H3）：f，f1∈C1（Ω×［0，∞）×R3）；

给定M＞0，T＞0，我们令：

K0＝K0（M，T，f）＝

sup｛|f（x，t，u，v，w）|：（x，t，u，v，w）∈A*（M，T）｝；

K1＝K1（M，T，f）＝

sup｛|fx|+|ft|+|fu|+|fv|+|fw|）

（x，t，u，v，w）：（x，t，u，v，w）∈A*（M，T）｝；

其中：

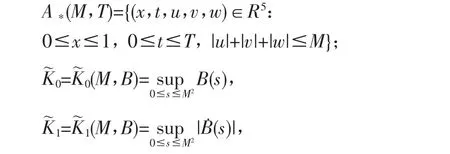
对每个M＞0，T＞0，我们有：

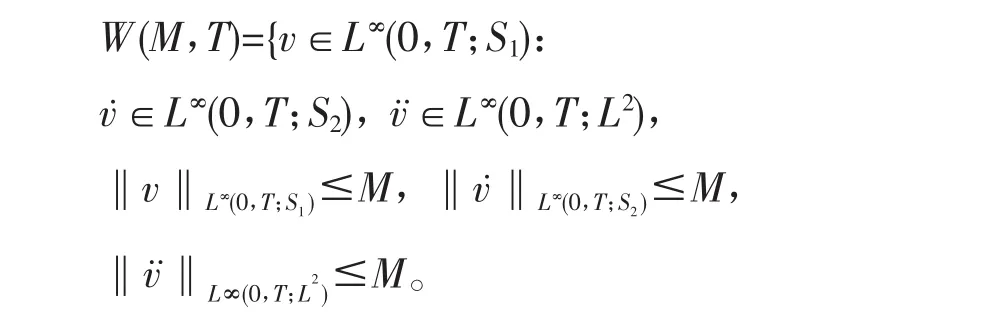
下面我们考察扰动问题（Pε）的弱解的存在唯一性。

定理假设（H1）～（H3）成立，则存在常数M＞0，和T＞0，使得对任意|ε|≤1，问题（Pε）有唯一弱解uε满足uε∈W（M，T）以及估计：其中C是依赖于M，T，0（M，B1），K0（M，T，f1），1（M，B），和K1（M，T，f）的常数。

证明 令ν＝uε-u0，则v满足以下变形问题：

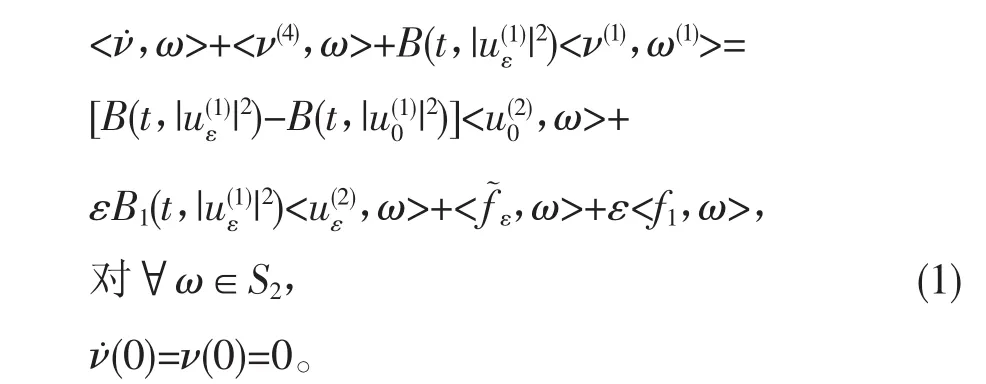
其中：

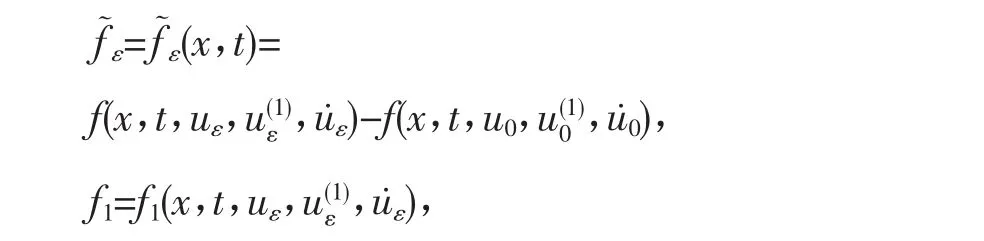
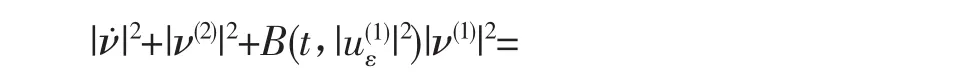
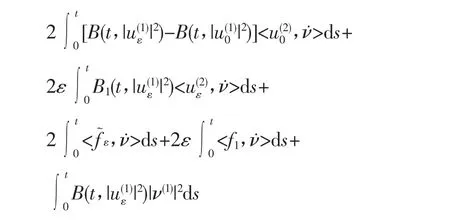
而

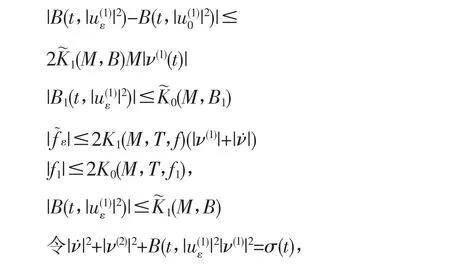
则

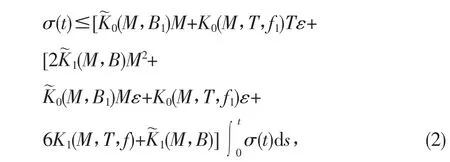
由（2）式及Gronwall′s引理，我们有：

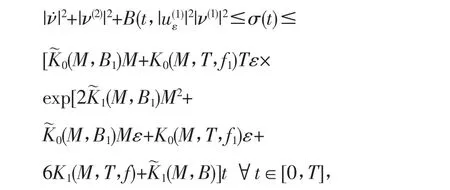
所以：

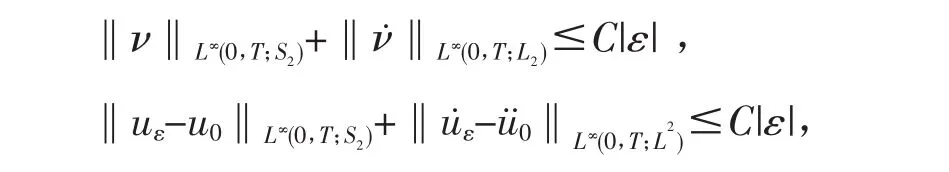
其中：

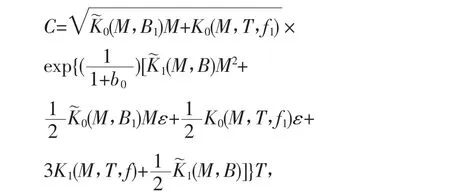
定理证毕。

［1］Long N T.On the nonlinear wave equation utt-B（t，|ux|2）uxx＝f（x，t，u，ux，ut）associated with the mixed homogeneous conditions［J］.J.Math Anal Appl.2002，274：102-123.

［2］Long N T，Dung B T.On the nonlinear wave equation utt-B（t，|ux|2）uxx＝f（x，t，u，ux，ut，|ux|2）associated with the mixed homogeneous conditions［J］.J Math Anal Appl，2004，292：433-458.

［3］Dickey R W.Free vibrations and dynamic buckling of the extensible beam［J］.J Math Anal Appl，1970，29：443-454.

［4］Pereira D C.Existence.uniqueness and asymptotic behavior for solutions of the nonlinear beam equation［J］.Nonlinear Analysis，TMA，1990，14（8）：613-623.

［5］陈金梅，王祥.一类非线性波动方程弱解的存在唯一性［J］.系统科学与数学学报，2011，31（8）：1-7.

〔责任编辑 高海〕

The Asymptotic Behavior of the Solution of the Wave Equation with Strong Damping

CHEN Jin-mei1，WANG Xiang1，ZHAO Huan-huan2，LIU You-jun2
（1.Department of Mathematics，Xinzhou Teachers University，Xinzhou Shanxi，034000；2.School of Mathematics and Computer Science，Shanxi Datong University，Datong Shanxi，037009）

In this paper，We considered the case of strong damping effect，established a class of the beam equation with axial loading.We studied the global solution of the perturbed problem of the nonlinear beam equation with strong damping.Sobolev space properties as a tool，We proved the existence of weak solutions of the perturbed problem.

nonlinear；the beam equation；the perturbed problem；the global solution

O175.27

A

1674-0874（2012）05-0019-02

2012-05-25

忻州师范学院自然科学基金［201124］

陈金梅（1979-），女，山西吕梁人，硕士，讲师，研究方向：偏微分方程。