含参量x的无界反常积分
李志广
(山西大同大学数学与计算机科学学院,山西大同 037009)
含参量x的无界反常积分
李志广
(山西大同大学数学与计算机科学学院,山西大同 037009)
现行教材中对于含参量x的无界反常积分,仅仅给出了定义,对此进一步探究,给出了其一致收敛的判别法。
无界;反常积分;一致收敛
1 预备知识
定义1设f(x,y)在区域R=[a,b]×[c,d)上有定义,若对x的某些值,y=d为函数f(x,y)的瑕点,则称

为含参量x的无界函数反常积分,或简称为含参量反常积分。若对每一个x∈[a,b]积分(1)都收敛,则其积分值是x在[a,b]上取值的函数。
定义2 对任给正数ε>0某正数δ<d-c,使得当0<η<δ时,对一切x∈[a,b],都有

则称含参量反常积分(1)在[a,b]上一致收敛。
2 一致收敛的判定定理
定理1 含参量反常积分(1)在[a,b]上一致收敛的充分必要条件是:对任给正数ε,总存在某正数0<δ<d-c,当0<η1<δ,0<η2<δ时,对于∀x∈[a,b]有,



(充分性)对任给正数ε>0,存在正数δ<d-c,当0<η1<δ,0<η2<δ时,对∀x∈[a,b]有:
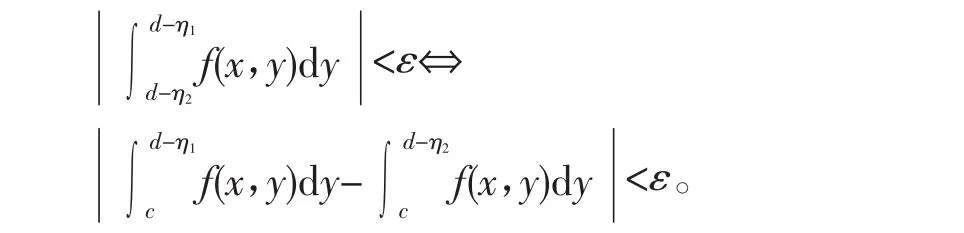
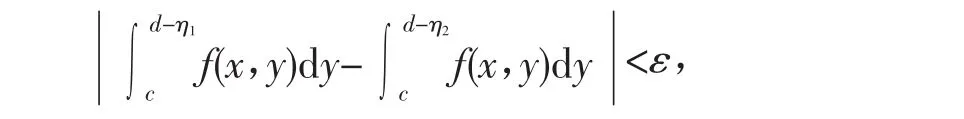
当η2→0时,有:

定理2 含参量反常积分(1)在[a,b]上一致收敛的充要条件是:对任一趋于d的递增数列{An}(其中A1=c),函数项级数

在[a,b]上一致收敛。
证明(必要性)由(1)在[a,b]上一致收敛,故对任给ε>0,必存在δ∈(0,d-c),对于0<η<δ,使得当A″>A′,且A″,A′∈(d-η,d)时,对一切x∈[a,b],总有

又由An→d(n→∞),所以对正数δ,存在正整数Ν,只需m>n>N时,就有Am>An>d-η,由(3)知,对一切x∈[a,b],就有
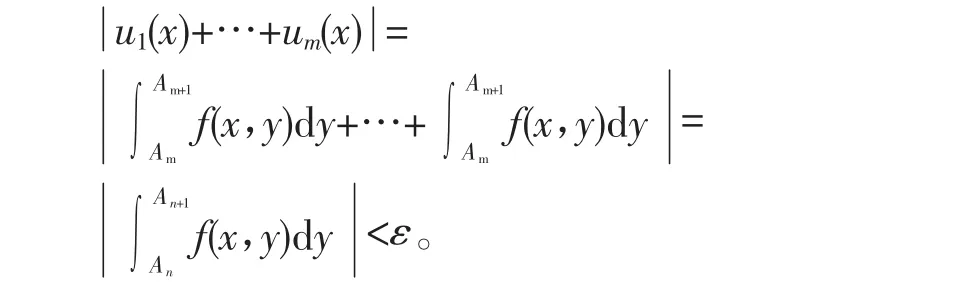
这就证明了级数(2)在[a,b]上一致收敛。
(充分性)用反证法。假设(1)在[a,b]上不一致收敛,则存在某个正数ε0,使得对于任何实数0<δ<d-c,存在相应的d-δ<A′<A″<d和x′∈[a,b],使得

现在取δ=min{1,d-c},则存在d-δ<A1<A2<d,以及x1∈[a,b],使得
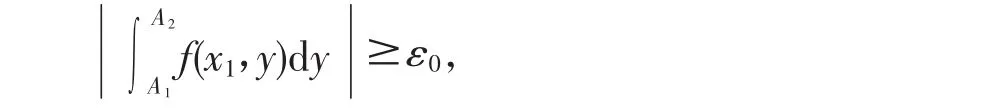



这与级数(2)在[a,b]上一致收敛的假设矛盾,故含参量反常积分(1)在[a,b]上一致收敛。
3 一致收敛的判别法

判别法2 设
(1)对一切实数c<N<d,含参量正常积分

对参量x在[a,b]上一致有界,即存在正数M,对一切c<N<d,以及一切x∈[a,b],都有

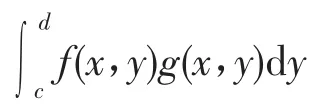

又因为对每一个x∈[a,b],函数g(x,y)关于y是单调递减且y→d时,对参数x,g(x,y)一致地收敛于0,故存在某一正数0<δ<d-c,使得对于一切d-δ<u1<u2<d,都有,

由上述可知,取M=max{N,d-c},对于一切M<u1<u2<d,都有,
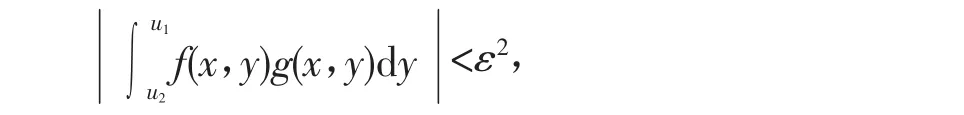
判别法3 设
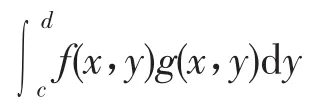
[1]张振祺.含参量反常积分局部一致收敛的判别法[J].榆林学院学报,2010,12(6):13-18.
[2]王建英.含参量非正常积分的局部一致收敛[J].集宁师专学报,2008,22(4):45-47.
[3]黄慧,陈辉.含参量无穷限反常积分的一致收敛性[J].高等数学研究,2011,2(1):7-10.
[4]裴礼文.数学分析中的典型问题与方法[M].北京:高等教育出版社,2006.
[5]陈纪修.数学分析[M].北京:高等教育出版社,2004.
[6]高建平,刘声,张蕊.反常积分收敛判别法[J].数学学习与研究,2010,19(9):23-31.
〔责任编辑 高海〕
Unbounded Improper Integral with Parameter
LI Zhi-guang
(School of Mathematics and Computer Science,Shanxi Datong University,Datong Shanxi,037009)
In current textbooks for unbounded improper integral with parameter,only definitions are given,in this article,on further inquiry,its uniform convergence criterion is given.
unbounded;improper integral;uniform convergence
O172.2
A
1674-0874(2012)05-0010-02
2012-03-15
李志广(1979-),男,河北阳原人,硕士,讲师,研究方向:分布参数系统。

