最值问题变中求新

☉江苏省沭阳高级中学 王东阳

长期以来，高三的数学复习是做大量的习题，搞多次模拟训练，学生逻辑思维能力和空间想象能力有一定的提高，但是分析问题和解决问题的能力提高甚少，结果是事倍功半，因此，如何激发学生的兴趣，培养学生勇于探索的习惯和创新能力，提高复习效果，做到轻负担、高质量，是十分重要的，所以需要研究复习方法，提高课堂效率，其中一题多变对培养学生的解题能力，提高学生的思维能力将大有益处.

变式1：函数f（x）=2x3-3x2-12x+5在区间［-2，3］上的最大值与最小值分别为（ ）.

A.12，-15 B.1，-4 C.12，4 D.5，-16

分析：求值域一般先求函数的最值.本变式与原题相比，解析式与自变量的取值区间都发生了变化.事实上，只要掌握了求函数最值问题的一般方法，不论自变量的取值区间、函数的解析式如何变化，解决问题的本质是一样的.

解：先求导数，得f′（x）=6x2-6x-12=6（x+1）（x-2），令f′（x）=0，解得x1=-1，x2=2，当x变化时，f（x），f′（x）的变化情况如下表：

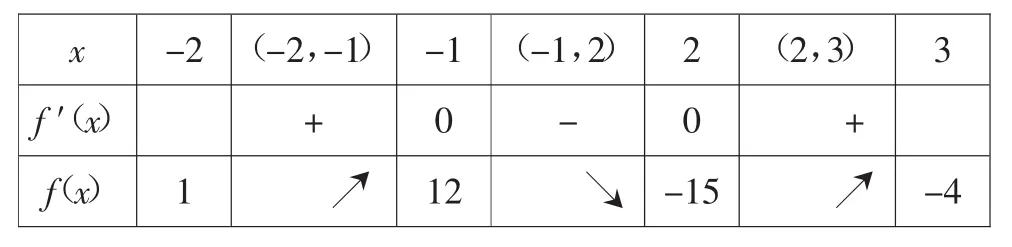
x -2 （-2，-1） -1 （-1，2） 2 （2，3） 3 f′（x）+0-0+f（x）1↗12↘-15↗-4

从上表可知，当x=-1时，函数取得最大值12，当x=2时，函数取最小值-15，故选A.

点评：求解闭区间的最值问题的一般步骤是：先求得该区间的极值点，然后求得极值点的函数值与端点处的值比较就可以得到该区间的最值.

变式2：已知函数f（x）=ax3-6ax2+b在区间［-1，2］上的最大值为3，最小值为-29，求a、b的值.

分析：本题与变式1的区别是已知最值逆向求参数问题，体现了数学中的待定系数法，可以先求导，然后比较，确定取得最大值和最小值的x的值，再代入求得a、b的值，要注意对a进行讨论.

解析：f′（x）=3ax2-12ax=3ax（x-4），在区间［-1，2］上，令f′（x）=0，根据题意a≠0.

当a>0时，函数f（x）在x＝0处取得极大值也就是最大值，比较f（-1），f（2）得：f（-1）>f（2），所以f（0）＝3，f（2）＝-29，解得a＝2，b＝3.

当a<0时，易知函数f（x）在x＝0处取得极小值，也就是最小值，且f（-1）

点评：本题从逆向思维的角度出发，根据题意逆向联想，通过建立最值点确立相等关系，运用待定系数法求出a，b的值.

分析：不等式f（x）-m≥0恒成立，即m≤f（x）对任意实数x∈［-3，6］恒成立，所以m满足m≤f（x）min，x∈［-3，6］即可.本题与变式1相比，难度有所加大，但只要分析出m≤f（x）min，x∈［-3，6］，问题便与变式1相差无几.

解：令f′（x）=x2-4，解得x=2或x=-2.由于，所以f（x）在区间［-3，6］上的最小值为，即（fx）在区间［-3，6］上的最小值为，所以m的取值范围为

点评：若在等式或不等式中出现两个变量，其中一个变量的范围已知，另一个变量的范围为所求，且容易通过恒等变形将两个变量分别置于等号或不等号的两边，则可将恒成立问题转化成函数的最值问题求解.分离参数法有时能减少讨论次数，甚至能避免讨论.

综上可得，实数m的值为4.

点评：本题从逆向思维的角度出发，根据题意逆向联想，通过建立最值点确立相等关系，运用待定系数法求出m的值.由于函数的根的大小没法确定，所以需要分类讨论.

变式5：已知函数f（x）=-2x3-3x2+12x+1在［m，1］上的最小值为-17，则m的值为_________.

分析：本题与上题最大区别是闭区间一端含有参数，首先需要求导数，然后比较最小值与极小值，从而确定参数m的范围，再利用方程思想求得m的值.

解析：因为f′（x）=-6x2-6x+12=-6（x+2）（x-1），令f′（x）=0，得x1=-2，x2=1，所以f（x）在（-∞，-2）上为减函数，在［-2，1］上为增函数，所以f（-2）为极小值，又因为f（-2）=-19，但在［m，1］上，f（x）min=-17，因为-2

点评：解决本题的关键是求出导函数的单调区间，明确函数的极值点，与函数的最值比较，确定m的范围，结合函数的最小值求得m的值.注意对m的值进行恰当的取舍.

综上，高三复习不是在同一水平上的简单重复，需要创造性地将知识、能力和思想方法在更多的新情境下、更高的层次中不断地、反复地渗透，才能达到螺旋式再认识、再深化乃至升华的结果.