例析数形结合的思想方法在解高考题中的运用
☉江苏省泰州市二中附中 曹文喜
我国数学家华罗庚曾说:“数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休.”数形结合是一种数学思想方法,在解题中要根据数学问题的条件和结论之间的内在联系,使数量关系的精确刻画与空间形式的直观形象巧妙、和谐地结合在一起,灵活地运用数形结合的思想方法,能使复杂问题简单化,抽象问题具体化.运用数形结合的方法解题,历来一直是高考考查的重点之一.举例如下:
一、利用数形结合研究集合问题
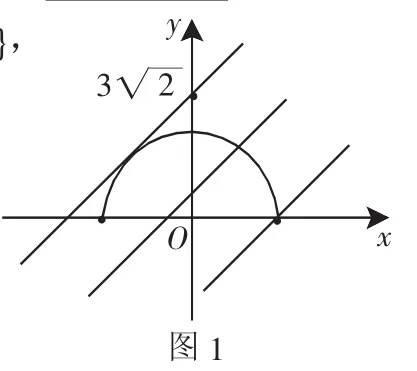
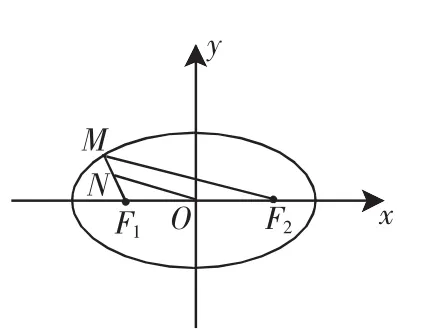
【解 析】M=({x,y)|x2+y2=9,0 【注】集合转化为点集(即曲线),而用几何方法进行研究.此题也属探索性问题用数形结合法解,其中还体现了主元思想、方程思想,并体现了对有公共点问题的恰当处理方法. 【解析】等式(x-2)2+y2=3有明显的几何意义,它表示坐标平面上的一个圆,圆心为(2,0),半径则表示圆上的点(x,y)与坐标原点(0,0)的连线的斜率.如此以来,该问题可转化为如下几何问题:动点A在以(2,0)为圆心,以为半径的圆上移动,求直线OA的斜率的最大值,由图2可见,当∠A在第一象限,且与圆相切时,OA的斜率最大,经简单计算,得最大值为 图2 【注】通过转化将此类问题变成求斜率最大值的问题是常见的也是最简捷的方法. 图3 【解析】设椭圆另一焦点为F2,如图3,则|MF1|+|MF2|=2a,而a=5,|MF1|=2,故|MF2|=8.又注意到N、O各为MF1、F1F2的中点,则ON是△MF1F2的中位线, 故 【注】若联想到第二定义,可以确定点M的坐标,进而求MF1中点的坐标,最后利用两点间的距离公式求出|ON|,但这样就增加了计算量,显得有些复杂. 例4 若方程lg(-x+3x-m)=lg(3-x)在x∈(0,3)内有唯一解,求实数m的取值范围. 【解析】将对数方程进行等价变形,转化为一元二次方程在某个范围内有实解的问题,再利用二次函数的图像进行解决,原方程变形为 图4 设曲线y=(x-2)2,x∈(0,3)和直线y=1-m图像如图4所示.由图可知: ①当1-m=0时,有唯一解,m=1; ②当1≤1-m<4时,有唯一解,即-3 故 m=1或-3 【注】此题也可设出曲线y=-(x-2)2+1,x∈(0,3)和直线y=m后画出图像求解. 图5 【解析】由于|z-2-2i|=|z-(2+2i)|,有明显的几何意义,它表示复数z对应的点到复数2+2i对应的点之间的距离,因此满足的复数z对应点Z,在以(2,2)为圆心,半径为的圆上(如图5),而|z|表示复数z对应的点Z到原点O的距离,显然,当点Z、圆心C、点O三点共线时,|z|取得最值,故|z|的取值范围为 【注】本题运用“数形结合法”,把共轭复数的性质与复平面上的向量表示、代数运算的几何意义等都表达得淋漓尽致,体现了数形结合的生动活泼.一般地,复数问题可以利用复数的几何意义而将问题变成几何问题,也可利用复数的代数形式、三角形式、复数性质求解. 数形结合的思想方法应用广泛,运用数形结合思想,不仅直观易发现解题途径,而且能避免复杂的计算与推理,大大简化了解题过程.平时教学时要注意培养学生的这种思想意识,做到胸中有图,见数想图,从而开拓学生的思维视野.二、利用数形结合求最值
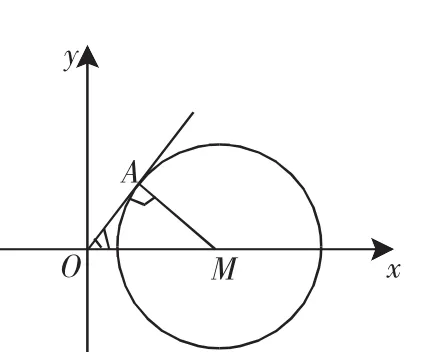
三、利用数形结合求线段的长
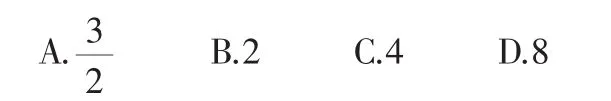
四、利用数形结合探究参数范围

五、利用数形结合解答复数问题


