向量运算：数与形一个也不能少

☉江苏省赣榆高级中学 张自勇

数学课上，万老师在黑板上写了两组题，分别交给两个兴趣小组的同学来做，做完后说说这组题的意图是什么，并谈谈自己的解题体会.

第一组题：向量的线性运算

例1 如图1，在△ABC中，∠BAC=120°，AB=2，AC=1，D是边BC上一点

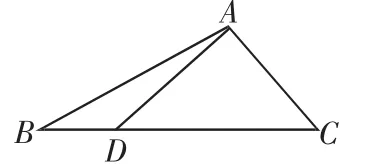
图1

万老师：这组题的运算特点是什么?

张超：这组题都与向量的线性运算有关，首先要选取不共线的两个向量作为基底，主要是选择知道线段的长度、夹角等线段，再用基底表示有关的向量，最后进行向量的加减法、数乘、数量积的运算.

第二组题：向量的坐标运算

例3 已知△ABC中，A（2，-1），B（3，2），C（-3，-1），BC边上的高为AD，求点D和向量的坐标.

马俊：本题建立坐标系，给出了点的坐标，可以通过向量的坐标运算来进行.

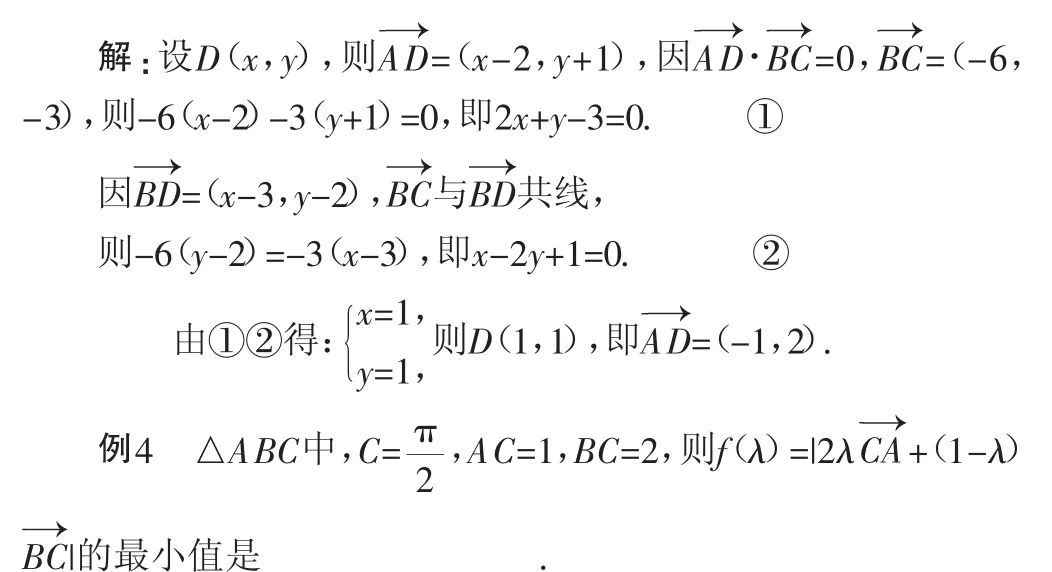
万老师：这组题的特点是什么？

马俊：这组题都是平面向量的坐标运算，题目建立了坐标系或较容易建立坐标系，再通过向量的坐标进行向量的加、减、数乘、数量积等运算.

万老师：向量是既有长度又有方向的量，向量的线性运算反映了向量的本质特征，更容易被同学们理解和接受.为了解决问题的方便，建立了平面直角坐标系，分别取x轴y轴正方向上的单位向量作为基底，使点的坐标与向量的坐标对应起来，从而大大简便了向量的运算.

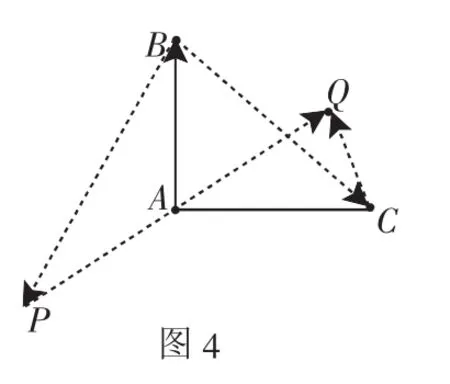
同学们，经过这两组题的学习，你对向量运算的理解想必更深刻了吧！那就试用两种方法解下面这道题：

练习：如图4，在Rt△ABC中，已知BC=a，若长为2a的线段PQ

错解分析：当2m2+m-1=0时，直线的斜率不存在，错解忽略了这一点.

六、误把截距等同于距离

例6 求过点A（-4，1），且在坐标轴上截距相等的直线l的方程.

错解：由题意得直线l的倾斜角α=45°.

则k=1，又过点（-4，1），

则直线l的方程为x-y+5=0.

错解分析：此解其中一个错误就是误把截距等同于距离，另一个错误是忽略了一种特殊情况——过原点的直线，它也符合在坐标轴上截距相等的条件.

正解：由题意得直线l的倾斜角为135°或过原点.

当α=135°时，k=-1，又因为过点（-4，1），所以直线l的方程为x+y+3=0；

当直线过（-4，1），（0，0）时，直线l的方程为x+4y=0.

综上所述，所求直线方程为x+y+3=0或x+4y=0.

七、直线方程的几种形式及其适用范围掌握不熟练而出错

例7 当a为何值时，直线l1：（a+2）x+（1-a）y-1=0与直线l2：（a-1）x+（2a+3）y+2=0互相垂直？

错解分析：直线方程的一般式包含了所有直线的方程，而斜截式只适用斜率存在的直线的方程，所以在把一般式化成斜截式时会漏解，做此类题目时应先考虑好斜率不存在的情况.

正解：当直线l1斜率不存在时，1-a=0，即a=1时，直线l1：3x-1=0与直线l2：5y+2=0垂直；

则a=-1.

综上所述，当a=1或a=-1时，l1⊥l2.

点评：本题还有更简洁的方法，通过推导出两直线垂直的一般性结论：A1A2+B1B2=0来做，不需要分类讨论，就可以避开斜率不存在或斜率为0的情况，是两直线垂直的充要条件.