分类加法计数原理与分步乘法计数原理（教学设计）

☉浙江省宁波市第四中学 邵春霞

一、教材分析

1.教材的地位与作用.

本节课教学内容是《分类加法计数原理与分步乘法计数原理》，是人教A版数学选修2-3第一章第一节内容.这两个原理是本章的重点基础知识，一方面它为后面学习排列、组合、随机变量的概率等内容提供了思想和理论依据，是学习排列组合e的基础；另一方面它的结论与其基本思想方法在解决本章应用问题时有许多直接应用，因此，它理应成为我们重点把握的教学内容.新旧教材最大区别在于：旧教材是先学习两个计数原理后学习概率，体现由理论到应用的过程；而新教材是在学习了古典概型的基础上提出了本节内容，体现了由实践到理论、再到实践的过程，学生在具备一定的计数能力（树形图、列举法等）和实例的前提下，能更好更快地体会两个基本原理的作用与适用范围，在实践中能更灵活地运用两个基本原理来解决问题，这样的设计能为学习构建牢固的知识框架打下基础.

2.教学重点与难点.

教学重点：对两个计数原理的认识与理解，并能解答简单的应用问题.

教学难点：准确区分加法原理与乘法原理.

二、教学目标

1.知识与技能.

（1）通过实例，总结出分类加法计数原理和分步乘法计数原理；

（2）能根据具体问题的特征，选择分类加法计数原理或分步乘法计数原理解决一些简单的实际问题.

2.过程与方法.

（1）经历提炼两个原理的过程，体会两个计数原理的意义；

（2）在寻找身边“分类”、“分步”计数问题的过程中体会两个原理的区别和联系；

（3）在解决实际问题的过程中，进一步体会将问题进行“分类”思考和“分步”思考的数学方法.

3.情感、态度与价值观.

（1）体会数学源于生活又服务生活；

（2）培养学生的归纳概括和自主学习能力；

（3）通过合作探究，培养学生勤于思考、勇于探索的精神.

三、教法分析

问题探究式教学.

四、学法指导

观察分析，分类讨论，比较归纳.

五、过程设计

1.创设问题情境，激发学习兴趣，导入课题.

背景资料1：如今宁波汽车保有量突破100万辆，驾驶证突破200万本.以760万常住人口计算，平均每4人，就拥有1本机动车驾驶证，平均每3户家庭，就有1辆汽车.按照国际通行说法，100万辆以上的汽车保有量，是一个城市进入“汽车社会”的标志.（2011-09-0810：37：38来源：新蓝网）

背景资料2：如果宁波市汽车牌照形式为“浙B-□□□□■”，其中“浙B”为地区代码，■为大写英文字母D，E，□为0～9阿拉伯数字.

请想一想：按此方式编排，最多有多少个不同的牌照？

【设计意图】要回答这个问题，就要用到排列、组合的知识.在运用排列、组合方法时，经常要用到分类加法计数原理与分步乘法计数原理.

2.从实例抽象出分类、分步加法计数原理.

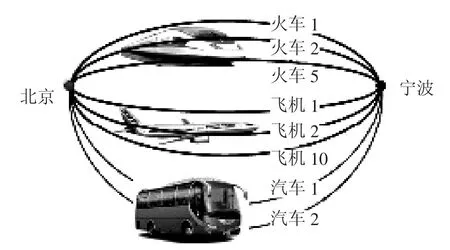
问题1：中国智能交通协会专家从北京到宁波进行学术交流，已知从北京到宁波，可以乘火车，也可以乘飞机.一天中，直达火车有5班，直达飞机有10班.那么一天中，乘坐这些交通工具从北京到宁波共有多少种不同的走法？

【设计意图】配图分析，引导学生得出坐火车与坐飞机两类办法均可，每类任一种办法都可以独立把从北京到宁波这件事情办好.

变式1：若从北京到宁波一天中还有2班汽车可乘，那么一天中乘坐这些交通工具从北京到宁波，共有多少种不同的走法？

变式2：做一件事，完成它可以有n类办法，在第一类办法中有m1种不同的方法，在第二类办法中有m2种不同的方法，…，在第n类办法中有mn种不同的方法，每一类中的每一种方法均可完成这件事，那么，完成这件事共有多少种不同的方法？

【设计意图】学生解答以上问题水到渠成，顺着变式2的解，不难由学生归纳出分类加法计数原理.

问题2：中国智能交通协会专家先乘飞机从北京到杭州，再于次日从杭州乘汽车到宁波.一天中，汽车有6班，飞机有10班，那么两天中，从北京到宁波共有多少种不同的走法？

【设计意图】配上插图，引导学生分析，组织讨论，引导学生模仿分类加法计数原理归纳得出分步乘法计数原理.

3.引导学生对两个原理加以应用.

例1 书架的第一层放有4本不同的计算机书，第二层放有3本不同的文艺书，第三层放有2本不同的体育书.

（1）从书架上任意取1本书，有多少种不同的取法？

（2）从书架的第一第二第三层各取1本书，有多少种不同的取法？

（3）从书架上任取2本不同学科的书，有多少种不同的取法？

【设计意图】这是一道用于巩固两个原理的例题，通过引导学生分析解答，使学生理解两个原理的区别.同时让学生总结得到：若“要完成的事”满足“类类独立”，用任何一类中的任何一种方法都能独立完成这件事情，则是一个分类问题；若“要完成的事”满足“步步相依”，只有依次完成每一个步骤才能完成这件事情，则是一个分步问题.

例2 用A，B和1—9九个阿拉伯数字以A1，A2，…，B1，B2，…的方式给教室椅子编号，能编出多少不同的号码？

【设计意图】让学生在解答过程中初步感知这些计数问题并不完全相同，介绍“树形图”是解决计数问题的的常用方法

例3 如果宁波市汽车牌照形式为“浙B-□□□□■”其中“浙B”为地区代码，■为大写英文字母D，E，□为0～9阿拉伯数字.按此方式编排，最多有多少个不同的牌照？

【设计意图】通过此例让学生体会到数学源于生活又服务生活，同时让学生明白解决数学问题的基本方法：从实际问题中提炼出数学概念，再用数学概念解决实际问题.

4.构建知识系统，掌握方法，强化能力.

（1）知识小结，学生回答后教师总结.

一个中心：计数问题.

两个基本原理：分类加法计数原理和分步乘法计数原理.

三个关键点：分析“完成怎样一件事”；区分“分类”或“分步”，“分类”满足“类类独立”，“分步”满足“步步相依”；注意分类标准要求“不重不漏”，分步标准要求“步骤完整”.

（2）运用数学思想方法，获取数学知识过程的小结.

两个基本原理体现了解决问题时将其分解的两种常用思想方法——分类解决或分步解决.

解决数学问题的基本方法：实际问题⇒数学概念⇒实际问题.

类比、发现、归纳、探索前进是创造的基本途径.

5.布置作业.用生活中的例子编写计数问题.

要求：

编一个题目；

涉及两个原理其中一个的计数问题；

把讨论结果写在纸上.