运动场上的概率问题

☉浙江省杭州余杭第二高级中学 徐国锋

随着人们生活水平的不断提高，体育运动正为越来越多的人所喜爱.体育运动的魅力在于力量、在于美、在于技巧、在于竞争精神，还在于悬念，而种种悬念的答案往往就隐藏在概率之中.运动场上的概率问题也成为各类考试中一类重要的问题.

一、抽签分组概率

例1 已知8支球队中有3支弱队，以抽签方式将这8支球队分为A、B两组，每组4支.求A、B两组中有一组恰有两支弱队的概率.

（间接考虑）3支弱队分在一组，共2C15种分组方法，因而，三支弱队在同一组的概率为

评析：涉及到平均分组、标号问题要注意防“重”.在平均分组不标号（即无顺序）时防“重”，即在分步依次分组后要除以所分组数的阶乘.如例1中，8个队不标号平均分为两组，不同的分组数不是C48种；若平均分组标号则在分组的基础上再乘以所分组数的阶乘，如例1中，分为A、B两组的方法数是种，不是种.

二、传球概率

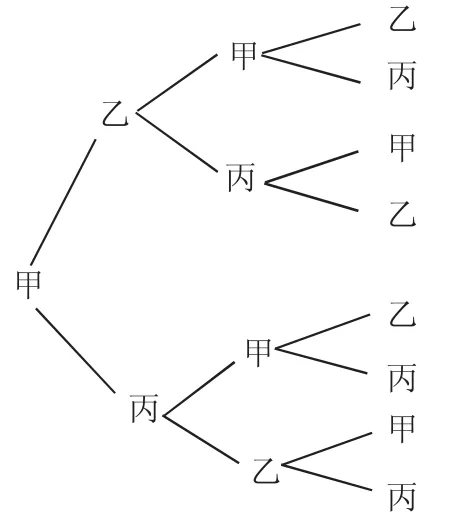
例2 甲、乙、丙三人做相互传球练习，第一次甲传给另外两人中的一人，第二次由拿球者再传给其他两人中的一人，…，且拿球者传给其他人种任何一人都是等可能的，求：

（1）第三次球传回到甲的概率；

（2）若规定：最多传五次球，且在传球过程中，球传回到甲手中即停止传球；设ξ表示传球停止时传球的次数，求P（ξ=5）.

解：（1）画出如下的树状图，第三次传递时共8（中）种不同的传递方式，其中传给甲的有2种，因而，第三次传递时甲得到球的概率为

再一种方法是按乘法原理考虑，分三步，最后球传给甲.甲在传球的过程中没接到球，即甲→非甲→非甲→甲，共有方法2×1×1=2种，总的传球方法为8种，即概率为

（2）注意在该问题中包含两种情形：最后甲得到球和甲一直没有得到球，其中，两种事件的个数都是2，因而，事件总数为16，

评析：利用树状图、列举法等是解决这类计数或概率问题的基本方法，不过，该类问题当传球人数或次数较多时，显然不易使用.第二种方法需要对问题合理转化，利用两个原理转化为纯粹的数学问题加以解决.该问题显然可以一般性的推广：明显在第n次传递时共有2n种不同的传递方式，其中在第2，3，4次传递时甲可以得到球的次数分别应为4-2，8-4，16-8，…，即22-2，23-（22-2），24-（23-（22-2））， 第n次传递时甲得到球的方式是2n减去第n-1次传递时球不在甲手中的情况，2n-2n-1+2n-2-…+（-1）n-12=再进一步推广，我们可以得到，满足例2条件的n个人传球，第k次传给甲的概率为

三、物品放置概率

例3 体育课后同学们把9个相同的足球随机地放入编号为1、2、3的三个箱子里（假定每个箱子都可以放下所有的球），则每个箱子放球的个数不少于其编号的概率是多少？

解：9个足球随机放入3个箱子中，共有39=19683种不同的方法，其中分别记1、2、3号箱子里的足球个数为x，y，z，则x+y+z=9，x≥1，y≥2，z≥3，转化为求不定方程的解的个数，再进行转化.令a=x，b=y-1，c=z-2，则a+b+c=6，a≥1，b≥1，c≥1，相当于把6个相同元素分成3份，每份不少于1个，用“插（挡）隔板”的方法即可，故所求概率为.不同的放法有22种.

评析：解题是智力竞技，需要基本功，也需要一定的技巧，该题主要是转化思想，把实际问题先转化为纯粹的数学问题：不定方程解，在数学范围内构造变形，然后再转变为实际问题模型，用“插隔板”的方法解决.

四、测试达标（命中）概率

例4 体育课进行篮球投篮达标测试，规定：每位同学有5次投篮机会，若投中3次则“达标”；为节省测试时间，同时规定：若投篮不到5次已达标，则停止投篮；若既使后面投篮全中，也不能达标（如前3次投中0次）则也停止投篮.同学甲投篮命中率为且每次投篮互不影响.

（1）求同学甲测试达标的概率.

（2）设测试中甲投篮次数记ξ，求ξ的分布列及期望Eξ.

解：（1）同学甲测试达标情况为，前三次都投中，前四次投中三次或者前四次中有两次投中第五次再投中，所以所求概率

（2）ξ的取值为3，4，5.ξ=3包含前三次全中或者全没有投中，，ξ=4包含第一次没投中前三次投中两次第四次再投中，或者前三次中有一次投中第四次没投中，表示前四次中投中两次第五次投中，或者前四次中投中两次第五次没投中

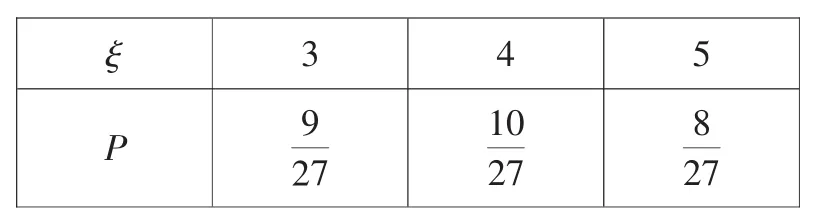
所以ξ的分布列：

ξ 3 4 5 P 9 2 7 10 27 8 2 7

评析：这类问题首先是分清楚随机变量的实际意义，把随机变量分解为基本事件的和事件，然后求出其相应的概率，特别是最后不能达标的情况，ξ=5时的情况是解这类问题的难点、易错点，要考虑两个互斥的事件，然后利用概率的加法公式确定这时的概率.

五、比赛场次概率

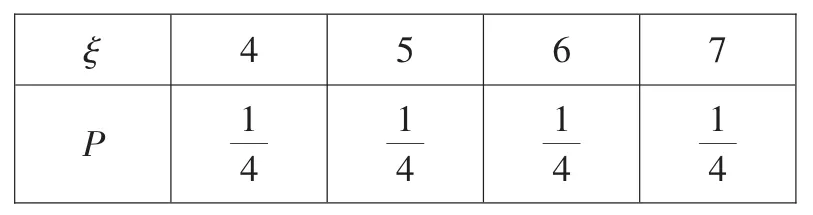
例5 甲、乙两人进行某项对抗性游戏，采用“七局四胜”制，即先赢四局者为胜，若甲、乙两人水平相当，且已知甲先赢了前两局，求：（1）乙取胜的概率；（2）比赛进行完七局的概率；（3）记比赛局数为ξ，求ξ的分布列及数学期望Eξ.

ξ 4 5 6 7 P 1 4 1 4 1 4 1 4

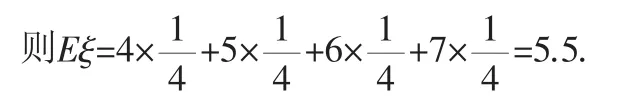
评析：分类讨论思想的正确运用是这类问题求解的根本，每一个问题都要根据实际情况分解成基本事件的和事件，在每一类问题中还可能需要把排列、组合方法与简单枚举方法结合起来.

六、赛场上金牌的概率

例6 2008年北京奥运会乒乓球比赛将产生男子单打、女子单打、男子团体、女子团体共四枚金牌，赛前保守估计，中国乒乓球男队获得每枚金牌的概率均为，中国乒乓球女队获得一枚金牌的概率均为

（1）求按此估计中国乒乓球女队比中国乒乓球男队多获得一枚金牌的概率.

（2）记中国乒乓球队获得金牌的数为ξ，试求ξ的分布列和数学期望Eξ.

解：（1）设中国乒乓球男队获0枚金牌，女队获1枚金牌为事件A，中国乒乓球男队获1枚金牌，女队获2枚金牌为事件B，则：

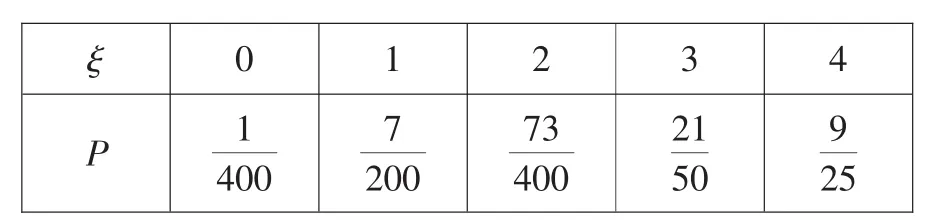
ξ 0 1 2 3 4 P 1 400 7 200 73 400 21 50 9 2 5

评析：夺金牌的根本在于实力，解题正确的根本在于扎实的基础、合理的策略和严密清晰地数学思想方法的运用.该问题突出分类讨论思想的运用，和对事件关系、互斥事件、积事件和事件概率等概念的准确理解.