导数压轴得分少,只因参数在『干扰』
2012-08-28 02:35湖北省监利一中万继方湖北省监利县朱河高级中学曾令平
中学数学杂志 2012年11期
☉湖北省监利一中 万继方 ☉湖北省监利县朱河高级中学 曾令平
纵览近些年的高考真题,不难发现函数与导数压轴题中总是有参数的参与,这基本上是它的基本特征.学生怕参数,感觉难以驾驭.事实上导数压轴题的解答过程确定让人眼花缭乱,其实含参问题的本质就是分类讨论.教师只需将常见的分类讨论类型一一介绍,并总结解决分类讨论的方法与注意事项,含参问题就能迎难而解了.
一、对判别式的讨论


二、对于根的大小进行讨论

当-1
当a<-1时,令f′(x)>0,解得x>-a,x<1,所以函数的单调递增区间为(0,1),(-a,+∞),递减区间为(1,-a).
三、对最高次系数的正负的讨论
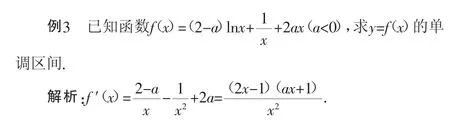

四、单调区间,极值与定义域的包含关系的讨论
例4已知函数f(x)=ax2-(a+2)x+lnx.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a>0时,函数f(x)在区间[1,e]上的最小值为-2,求a的取值范围.



综上可得a≥1.
前面列举了最为常见的几种类型,其中的关键是要对参数进行分析讨论.在具体讨论过程中,要特别注意以下几点:
1.思维严密,弄清楚分类讨论的原因与类型;
2.分类讨论要不重不漏;
3.最终结果的书写规范;
4.有些含参问题要估计其范围,从而确定其位置,达到不分类讨论的目的.
猜你喜欢
中学生数理化(高中版.高二数学)(2022年4期)2022-05-25
初中生学习指导·中考版(2022年4期)2022-05-12
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
中学生数理化(高中版.高二数学)(2021年4期)2021-07-20
新世纪智能(数学备考)(2021年11期)2021-03-08
新世纪智能(数学备考)(2020年11期)2021-01-04
中等数学(2020年7期)2020-11-26
中学生数理化·高一版(2019年9期)2019-10-12
中学数学杂志(初中版)(2019年4期)2019-09-18
中学生数理化·中考版(2018年9期)2018-11-09

