高考数学解题思想方法及应考技巧漫谈

☉宁夏回族自治区盐池高级中学 李彦鹏

根据《2012年普通高等学校招生全国统一考试大纲说明》的考核目标与要求，以能力立意的命题原则尝试以下三方面的新命题原则：

一是以数学内容为基点，以基本的推理能力和思维要求为出发点，突出考查学生一般能力的表现，测量学生的学习能力.

二是以多元化、多途径、开放式的设问背景，全面测量学生观察、实验、联想、猜想、归纳、类比、求异创新思维.

三是以源于社会、源于生活的问题考查学生.有效测量学生抽象、概括、建模能力.认识世界、把握本质、灵活运用所学知识分析问题、解决问题能力提出要求.上述新的命题原则是教育部考试中心评论专家任子朝先生总结的规律，对备考复习，应考具有一定指导价值.

在临近高考的冲刺阶段，考生要分清考试与平时的学习是不一样的，明确高考的地位及考查形式，高考不仅要考查知识掌握的程度，更重要地是要考查能力.因此平时学习好的同学不一定就能考好，只有掌握考试的技巧，展现自己的能力，方可轻松获取高分.本文结合高考和教学的实践谈几种运用较广泛而有效的解题思想方法，仅供参考.

一、数形结合，直观求解

数形结合就是根据数学问题的条件和结论之间的内在联系，既分析其代数意义，又揭示其几何直观，使数量关的精确刻划与空间形式的直观形象巧妙、和谐地结合在一起，充分利用这种结合，寻找解题思路，使问题化难为易、化繁为简，从而得到解决.其实质是将抽象的数学语言与直观的图像结合起来，关键是代数问题与图形之间的相互转化，它可以使代数问题几何化，凸显直观巧解题.

例1 已知点A（0，2），B（2，0）.若点C在函数y=x2的图像上，则使得△ABC的面积为2的点C的个数（ ）.

A.4 B.3 C.2 D.1

解析：如图1，观察到点O在抛物线上，且三角形OAB的面积为2，以AB为底边在两侧做平行线交抛物线共4个点即为所求，选A.本题抓住O点特殊性，借助几何直观，数形结合，是问题化难为易，从而快速求解.

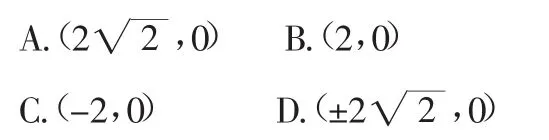
图2

二、把握一般与特殊思想

通过对某些个例的认识，积累对这类事物的了解，由现象到本质，由实践到理论；再用所得的规律解决这类事物中的问题.这种由特殊到一般，再由一般到特殊的反复认识过程就是人们认识世界的基本过程之一.在高考考题中，常常突出体现特殊化的方法.

例3 设等差数列{an}前n项和为Sn，若S9=72，则a2+a4+a9=_______.

解析：一般方法，令等差数列首项为a1，公差为d则由等差数列的前n项和公式得：9a1+36d=72⇒a1+4d=8，a2+a4+a9=3（a1+4d）=24.此法体现了方程思想，整体代入意识；遵循特殊化的方法，S9=72就是8与9的积为72，因此满足等差数列的公差d为0，即每一项均是8，所以a2+a4+a9=24.这里一般的方法当然是通性通法，这是我们在平时教学，高考复习都是极力提倡的，但这只是思考的角度不同而已，笔者在这里想说明，人们认识事物的科学方法之一，从一般到特殊再由特殊回到一般到反复过程，不是独立地搞特殊法，不是钻题目的空子，应考时我们不能及时想起来.培养的这种意识，并提升为数学思想即特殊与一般思想.

例4过抛物线y=ax2（a>0）的焦点F作一直线交抛物线于P、Q两点，若线段PF与QF的长分别是p、q，则等于（ ）.

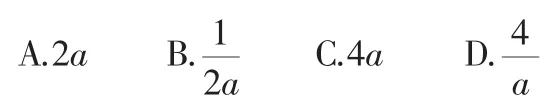
图3

解析：如图3，如果直接求解，有困难，联想抛物线的定义性质，由p，q向准线作垂线，再进一步求的值，还是不简单.如果把焦点弦PQ移动为平行于x轴，依据抛物线的方程求出交点F的坐标，代入抛物线方程求出F点点横坐标，立即求出体现了一般问题的特殊性，抓住特殊性就抓住了事物的特点，充分显示特殊与一般密切关系，突出思想，体现灵魂.

解析：如果依据题目画出一个一般的三角形的外接圆，作出高的交点H，标出圆心O，分析求解，面临困难.但若把三角形画成直角三角形如图4所示，问题易于求解.这时外接圆的圆心O在斜边中点O上，三角形两边高的交点与直角顶点C重合，则有，因此，某些数学问题，特别是数学选择题，它的考查功能有时只是能作出判断即可，不是搞研究，而正确快速作出判断，这当然是长期积淀的结果，但也存在一定的技巧，那就是要具备一般与特殊的思想.每个人都要自己的知识漏洞、缺陷，关键要保持平常的心态对待缺陷造成的错误，甚至能够珍惜之，有些数学问题不能及时解决，但并不意味着毫无机会，看起来困难，或许有机会做对.依靠的不是偶发的灵感，更重要的是对数学基本思想彻底理解.

图4

三、某些函数问题模型化，使问题明朗简单

数学是刻画自然规律和社会规律的真理，其本身就是简洁优美的.数学的语言是抽象的，形式化，符号化是它的特点.一方面，我们要做到准确理解数学概念、定理、公式等，另一方面，我们要处理数学问题时，要把复杂的简单化，深入浅出，使学生明白了才能认识数学，从而提升学生的解题能力.教师在教学实践中，要引导学生发掘数学的简单美，逐渐理解数学形式化语言，把握数学的实质.把数学问题模型化，特别是数学的核心问题之一即函数问题，确实不失为我们追求真理的一个有效方法.

解析：观察题目的条件，由x∈R都有f（x1）≤f（x）≤f（x2）成立，让余弦函数的自变量x取一些数值，根据余弦函数图像的有界性，所以，f（x2）是最大值，f（x1）是最小值.当f（x）取最值时，自变量x有无穷多，则|x1-x2|就是函数取最值时相应自变量x1，x2之间的距离，又由于求其最小值，因此，|x1-x2|表示自变量x1，x2同时取到最值时的相邻之间的距离即表示余弦函数的半个周期，所以，其最小值是2.这就是把该问题模型化，当看明白数学抽象符号下的性质内涵，问题就变的简单明了，迎刃而解，在具体分析探究过程中，培养了学生的概括整合能力.

解析：本题的编写初衷是应用抽象函数的周期性，反复迭代去求解，考察学生对函数周期性的掌握情况及相关的运算代换变形能力.如果把次问题模型化，则由4f（x）f（y）=f（x+y）+f（x-y）（x，y∈R）联想到所学的基本初等函数构建模型是：2cosxcosy=cos（x+y）+cos（x-y），得到f（x）应该是一个余弦函数，不妨令f（x）=Acosωx显然此解法十分简捷，一般问题模型化，看清问题实质，因此，教学要求就是要求学生在教师的引导下，立足教学实际，能提出问题，抓住事物的特点，不受习惯思维的约束，体现解决问题地深刻性和灵活性，并具有创造性.

总之，解答高考数学问题，特别是填空选择题目.一是要数形结合，直观求解；二是通过深入分析，多方联想，把握一般与特殊的思想；三是创造性地运用数学思想方法，找到问题特别是函数问题，模型化，使复杂问题简单明朗.或退到我们熟悉的问题上，看清问题的本质，迅速破解，对提高考生成绩具有积极的作用和帮助，我们期待2012年高考应考学子取得自己理想的成绩.