基于学生视角的“用形解数”教学

☉浙江省余姚市第四中学 鲁建桥

调查发现，“用形解数”因为可以直观、迅捷地解决某些代数问题，而深受学生的喜欢.但是，喜欢并不等于容易掌握，很多学生认为“用形解数”这种方法技巧性过强、不容易想到，而且一不小心就会犯错.基于学生对“用形解数”这种方法的认识，笔者认为，在教学过程中应从学生的困惑入手，关注以下两方面的问题.

一、“数”中思“形”，活用“基本几何模型”

在高中阶段的学习过程中，因为解析几何学科的开设，“用数解形”相对于“用形解数”使用更为普遍.然而，解析几何中的一些公式与方程，例如，直线斜率直线截距ax+by、距离公点到直线，还有向量的模长与夹角公式等等都可以作为沟通数形间关系的桥梁，实现“数”向“形”的转化，在这里我们将它们称为“基本几何模型”.学生如果熟练掌握这些“基本几何模型”，不仅可以丰富代数式的几何意义，而且可以利用“基本几何模型”解决一些相对复杂的代数问题.

例1 求证：（a1b1+a2b2）2≤（a12+a22）（b12+b22）.

上述问题的证明并不困难，但我们可以利用“基本几何模型”，丰富代数式的几何意义.

上述问题若用代数方法求解，计算较烦，花时较多.但如果充分利用“基本几何模型”，将表达式适当变形，将问题转化，我们可以挖掘代数式的几何意义，简化求解过程.

在平时的教学过程中，我们应帮助学生掌握“基本几何模型”，引导学生将复杂代数式进行化归，从不同角度挖掘代数式所具有的几何意义，体现数学问题解决的一般过程.同时，在教学过程中，老师也应向学生暴露思维过程，揭开“用数解形”的神秘面纱.

二、“形”来助“数”，把握教学契机

A.1 B.2 C.3 D.4

上述问题“用形解数”并不是最明智的选择，但是因为是解的个数问题，学生比较容易想到作出函数y=f（x）和函数y=x的图像判断交点个数，易错选B.究其原因，作草图不好判断抛物线与斜直线（不垂直于坐标轴的直线）的交点个数.这个时候，老师不应否定学生的做法，而是引导学生将问题转化为f（x）-x=0，从而考查函数y=f（x）-x和x轴的交点个数问题，学生容易作出正确的选择，答案为C.

例4 已知方程2x-1+2x2-a=0有两根，则a的范围是______.

此题出现在近期高三复习资料中，设计者的意图是强化函数与方程的联系，突出数形结合这一重要思想.

面对上述问题，学生容易形成共识：（1）此方程不能用常法判断；（2）可以转化为函数f（x）=2x-1和g（x）=-2x2+a的图像的交点个数判断.因此作出相应的图像（如图1），得到结论.这样的结果跟资料提供的答案一样，但事实上是不正确的.

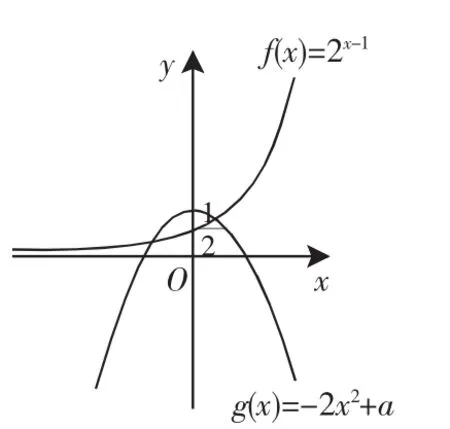
图1

这个时候，我们面对的是一个没有确切答案的问题，但却是帮助学生正确掌握“用形解数”这种方法的一个契机.我们不妨引导学生进行思考、质疑：函数f（x）=2x-1的图像和函数g（x）=-2x2+a的图像真的像我们所作的图1那样吗？它们会不会相切于某一点呢？

事实上，两函数图像会相切于一点，记为P.那么过P点存在两函数图像的公切线l（如图2）.利用这条切线的斜率可以建立关于x0的方程，从而只需求解x0即可.

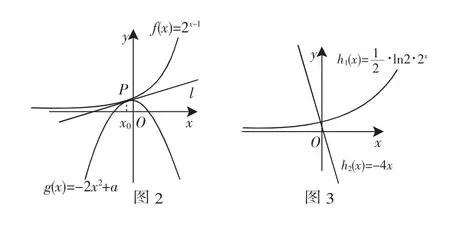
简解如下：设点P的坐标为（x0，y0），则有注意到此方程不能直接求解，则再作出函数和的草图（如图3）.我们不难发现两函数图像在第二象限有交点，即存在x0<0满足方程那么a的范围应该是a>2x02-4x0.

我想通过这个问题的质疑与探究，学生肯定能够进一步认识到：画出函数图像的确能使问题变得直观具体，但是我们只有借助对“数”的精确分析才能准确地刻画“形”的细微变化，从而更好地掌握“用形解数”这种方法.

我们不难发现：很多学生在运用“用形解数”这种方法解决代数问题的过程中，经常表现出用随意性的草图来刻画代数问题，从而导致最后不能准确地解决相关问题.这个现象提醒我们在我们平时的课堂教学应特别注意这一问题.比如在作正弦函数y=sin x和正切函数y=tan x的图像时，能够借助直线y=x来画，体现当时三者所具有的关系：sin x

既然“用形解数”是学生喜欢的数学方法，既然学生在运用这种方法的时候还有困惑与困难，那我们就应该从学生的视角去理解他们所面临的问题，开展针对性的教学，只有这样，才能帮助学生做到从“喜欢”到“掌握”，才能让“形”为“数”插上轻盈的翅膀.