浅议立体几何最值问题的处理方略

☉江苏省灌南高级中学 徐子娟

立体几何中有关角、距离、面积、体积等最值问题频频出现在近年的高考试卷中，此类问题涉及的知识面广，灵活性强.笔者通过对近年来高考题中几个典型的例题进行分析，浅谈这类问题的处理方略，供参考.

一、定性分析法

例1 已知在半径为2的球面上有A、B、C、D四点，若AB=CD=2，则四面体ABCD的体积的最大值为（ ）.

点评：本题中由于AB的长是定值，所以当三角形PCD的面积取最大值时，四面体ABCD的体积最大；于是本题可转化为求三角形PCD中CD边上的高h的最大值问题.

二、定量分析法

例2（2011山东卷理）在如图1所示的几何体中，四边形ABCD为平行四边形，∠ACB=90°，EA⊥平面ABCD，EF∥AB，FG∥BC，EG∥AC，AB=2EF.

（1）若M是线段AD的中点，求证：GM∥平面ABFE；

（2）若AC=BC=2AE，求二面角A-BF-C的大小.

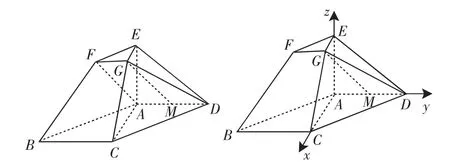
图1图2

解析：（1）如图1所示，连接AF，可证得FG∥AM且FG=AM.

所以四边形AFGM为平行四边形，因此GM∥FA.又FA⊂平面ABEF，GM⊄平面ABEF，所以GM∥平面ABFE.

（2）分别以AC、AD、AE所在直线为x轴、y轴和z轴，建立如图2所示的空间直角坐标系.

因此二面角A-BF-C的大小为60°.

点评：本题涉及二面角，条件之间的关系不容易发现；利用向量法可以将两个面之间的关系有机地连接起来，运算较为简便.

三、基本不等式法

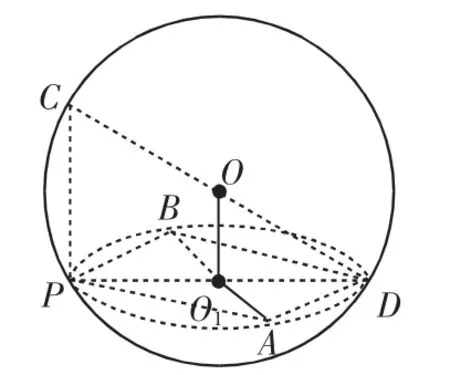
图3

例3 如图3，过半径为R的球面上一点P作三条两两垂直的弦PA、PB、PC.

（1）求证：PA2+PB2+PC2为定值；

（2）求三棱锥P-ABC的体积的最大值.

解析：（1）设过PA、PB的平面截球得⊙O1.由PA⊥PB，得AB是⊙O1的直径.连接PO1并延长交⊙O1于D，则四边形PADB是矩形，PD2=PA2+PB2.设O为球心，则OO1⊥平面⊙O1.由PC⊥⊙O1所在平面，得OO1∥PC，因此过PC、PD的平面经过球心O，截球得大圆.又PC⊥PD，则CD是球的直径.故PA2+PB2+PC2=PD2+PC2=CD2=4R2，为定值.

（2）设PA、PB、PC的长分别为x、y、z，则三棱锥P-ABC的体积

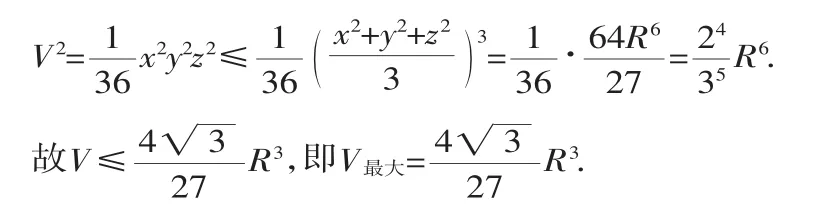
点评：本题新颖灵活，综合性较强，需用基本不等式进行求解.在均值不等式的应用中要注意应用条件.

四、导数法

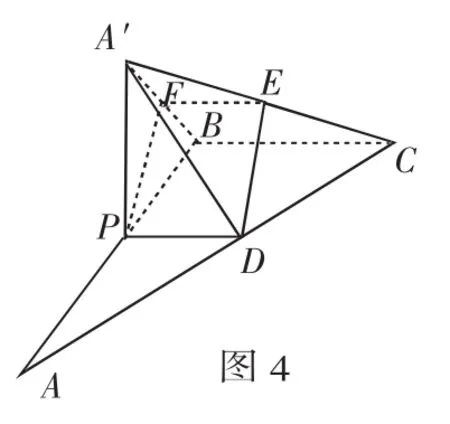
（1）当棱锥A′-PBCD的体积最大时，求PA的长；

（2）若点P为AB的中点，E为A′C的中点，求证：A′B⊥DE.

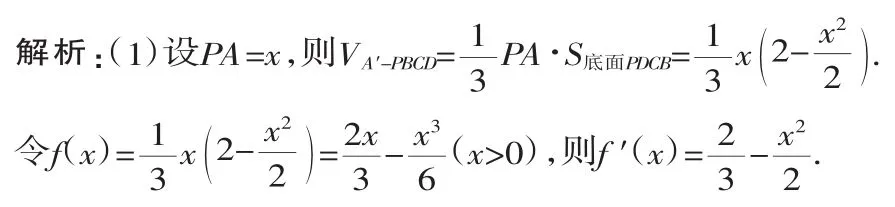
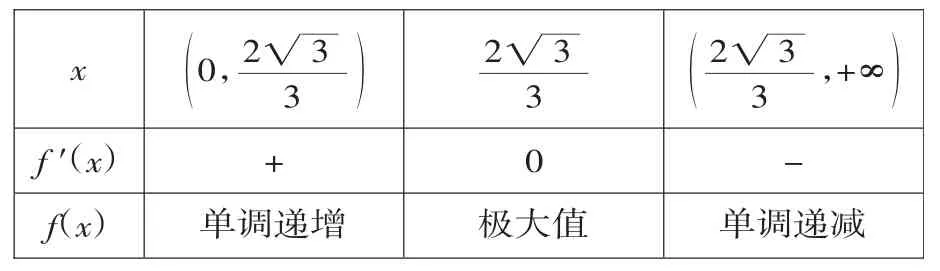
x 0，2 3■3（ ）233 2 3■3 ，+∞（ ）f′（x）+0-f（x）单调递增极大值单调递减

△A′PB为等腰直角三角形，A′B⊥PF，所以A′B⊥DE.

点评：从近年来全国高考命题形势看，在立体几何中渗透变量思想，而随着导数学习的深入，利用导数处理函数的最值问题已经成为重要手段，那么在立体几何中利用导数处理最值问题是一种很好的尝试.本题不同于前面的试题，它的亮点在于本题尽管用到导数但是仍然属于立体几何计算和证明题，这一点比起其他试题具有更加鲜明的特色.