立体几何中点的位置探索问题的解题策略

☉湖北省襄阳市第五中学 谢 伟

立体几何中关于点的位置的探索性问题是高考立体几何的热点和难点，由于这类问题不仅具有较强的趣味性、灵活性和隐秘性，而且问题情境新颖，解法灵活多变，因而能够很好地考查学生对基础知识的掌握情况，考查学生分析问题、解决问题的能力.下面以近年高考试题为例谈谈这类问题的解题策略.

一、观察图形，直接探究

例1 （2011年浙江理）如图1，在三棱锥P-ABC中，AB=AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上，已知BC=8，PO=4，AO=3，OD=2.

（1）证明：AP⊥BC；

（2）在线段AP上是否存在点M，使得二面角A-MC-B为直二面角？若存在，求出AM的长；若不存在，请说明理由.

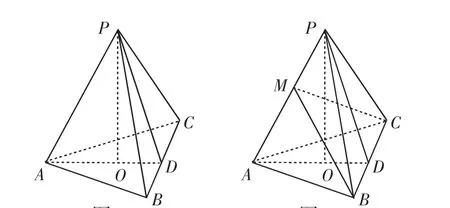
图1图2

分析：观察图形可以发现BC⊂平面BCM，AP⊂平面ACM，结合已证明的AP⊥BC，根据直线与平面垂直的判定定理，只需要BM⊥AP，就可以得到AP⊥平面BCM，再根据平面与平面垂直的判定定理可知，平面ACM⊥平面BCM.因此，点M的位置是过点B作AP的垂线的垂足.

解：（1）略；

（2）如图2，在平面PAB内作BM⊥PA于M，连接CM，由（1）知AP⊥BC，则AP⊥平面BMC.又AP⊂平面APC，所以平面BMC⊥平面APC.在RtPO2+OD2，在Rt△PBD中，PB2=PD2+DB2，所以，PB2=PO2+OD2+DB2=36，则PB=6.在Rt△POA中，PA2=AO2+OP2=25，则PA=5.cos∠BPA=从而PM=PBcos∠BPA=2，所以AM=PA-PM=3.

综上所述，存在点M符合题意，AM=3.

评注：解题的关键是观察出BC⊂平面BCM、AP⊂平面ACM和线线垂直（AP⊥BC）的图形特征，结合相关定理可知只需要BM⊥AP，根据试题的已知条件执因索果，找到满足条件的点.

二、执果索因，反溯探究

例2 （2010年辽宁文）如图3，棱柱ABC-A1B1C1的侧面BCC1B1是菱形，B1C⊥A1B.

（1）证明：平面AB1C⊥平面A1BC1；

（2）设D是A1C1上的点，且A1B∥平面B1CD，求A1D ∶DC1的值.

图3图4

分析：如图4，由于过A1B的平面A1BC1与平面B1CD相交于直线DE，要使得A1B∥平面B1CD成立，根据线面平行的判定定理，只需要A1B∥DE即可，而问题是：A1B∥DE是否成立呢？根据线面平行的性质定理，既然A1B∥平面B1CD，那么A1B∥DE必然成立，说明思考的方向是正确的.再注意到点E是BC1的中点，易知点D是A1C1的中点.

解：（1）略.

（2）如图4，设BC1交B1C于点E，连接DE，则DE是平面A1BC1与平面B1CD的交线，因为A1B∥平面B1CD，根据线面平行的判定定理，A1B∥DE.又E是BC1的中点，所以，点D是A1C1的中点.即A1D ∶DC1=1.

评注：本题解题的关键是执果索因，反溯使得结论成立的条件，其中直线与平面平行的判定定理和性质定理为寻找到解题突破口提供了保证.

三、代数方法，推理探究

例3 （2011年福建理）如图5，四棱锥P-ABCD中，PA⊥底面ABCD，四边形ABCD中，AB⊥AD，AB+AD=4，

（1）求证：平面PAB⊥平面PAD；

（2）设AB=AP，

（i）若直线PB与平面PCD所成的角为30°，求线段AB的长；

（ii）在线段AD上是否存在一个点G，使得点G到点P、B、C、D的距离都相等？说明理由.

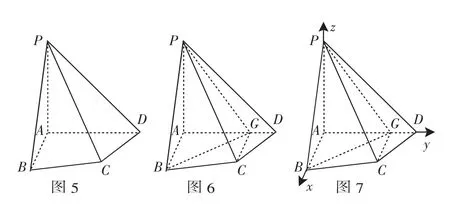
例3的代数方法的分析：存在型探索性问题一般先假设“对象”存在，然后根据题设探求可能的对象，并进行验证或者否定.由于点G是在线段AD上，因此，根据GC=CD和∠GDC=45°可以确定线段AD上到点D距离为1的点是点G的唯一可能的位置.剩下的任务就只是确认点G到其他点的距离是否也是1即可.

例3的代数解法：（1）略.

（2）（i）AB=0.8（过程略）.

（ii）如图6，假设在线段AD上存在一个点G，使得点G到点P、B、C、D的距离都相等，由GC=CD，得∠GCD=∠GDC=45°，从而∠CGD=90°，即CG⊥AD，GD=CD·sin45°=1.设AB=λ，则，这与GB=GD矛盾.所以，在线段AD上不存在一个点G，使得点G到点P、B、C、D的距离都相等.

评注：代数方法是解决几何问题的常用思想方法，体现了数形结合的思想，对于用几何方法直接求解比较困难的问题可以考虑用代数方法解决.

四、向量方法，计算探究

例3的向量方法的分析：在假设“对象”存在之后，由于点G的不确定性，直接验证或者否定点G都比较困难.在这种情况下，可以、建立空间直角坐标系，利用向量方法求解.

例3的向量解法：（ii）以A为坐标原点建立空间直角坐标系A-xyz，如图7，设AB=AP=t，则B（t，0，0），P（0，0，t），由AB+AD=4，得AD=4-t，所以C（1，3-t，0），D（0，4-t，0）.假设在线段AD上存在一个点G，使得点G到点P、B、C、D的距离都相等，设G（0，（2），由（1）、（2）消去t，化简得m2-3m+4=0（3）.由于方程（3）没有实数根，因此，在线段AD上不存在一个点G，使得点G到点P、B、C、D的距离都相等.

评注：向量方法是解决立体几何问题的基本方法，运用向量方法解题时，要注意根据几何图形特点建立合适的坐标系，并且要细心运算，防止运算出错，这是用向量方法解题的关键.