在数学教学中培养学生的辩证思维

☉江苏省睢宁高级中学（南校） 张大成 黄安成（特级教师）

这个话题，本不该有争议，但鉴于数学教学的时间紧、内容多、负担重、难度大，许多数学教师在实践中感到“无暇顾及”这个重要任务.更有甚者，认为数学教的只能是数学，不应该去管数学以外的“闲事”，学生也不懂什么辩证思维，讲了也白讲，既耽误了宝贵的教学时间，又很难取得成效，不如多处理一些题目来得实惠.所以对这个话题极有必要进行深入的探讨和研究.

1.在数学教学中培养学生辩证思维的必要性

恩格斯说：“数学中充满了辩证法”，“数学：辩证的辅助工具和表现形式”［1］，所以《普通高中数学课程标准（实验）》［2］要求学生“具有一定的数学视野，逐步认识数学的科学价值、应用价值和文化价值，…，从而进一步树立辩证唯物主义和历史唯物主义世界观.”

学生在初中阶段，已经学得了一点逻辑思维的基本原理与方法，但由于心理的稚嫩、思维水平与能力的薄弱、认知能力的局限、知识面的狭隘、生活阅历的贫乏、对人生及世界认识的肤浅与片面，辩证思维对于他们来说几乎是一片空白.而高中阶段则是他们的人生观与科学世界观逐步形成的关键时刻，他们将要经历的应该是从幼稚到成熟、从蒙昧到觉醒的成长、成熟的过程.在此过程中继续提高他们的逻辑思维水平，反复进行分析与解决问题的技能训练，固然是十分重要的，但在他们的综合素质中应该含有辩证思维的水平与能力.高中的政治教学当然应首先担负起这个重任，而作为理科之首的数学，也应该义不容辞地与政治教师“并肩协同作战”，而且由数学教师充分利用数学教学资源当此重任，具有的是鲜明的数学特色，在某些方面甚至还可以取得政治教学难以取得的上佳效果.

2.在数学教学中培养学生辩证思维的可行性

2.1 数学教材中含有大量可资利用的素材

数学中充满了辩证法，高中数学教材中也充满了辩证法.若舍弃不用，则是资源的浪费和良机的丧失.说严重一点，更是数学教师的失责.关键问题是须做到抓住契机、有机结合、巧妙揭示.

2.2 深入浅出的教学可取得良好的效果

别担心学生“不懂”，只要利用教学内容中鲜活生动的实例，用贴近学生思维、知识和生活的语言，深入浅出地进行讲解，学生的思维和思想定会与教师产生可喜的共鸣，深刻的道理就会变得浅显，通过内化，就变成他们自己脑海中的组成部分.数学教师来做这件事，学生将更加感到兴趣盎然.

2.3 辩证思维也有助于学生数学素养的优化

在许多概念的教学和问题解答的过程中，辩证思维的培养和数学素养的优化是融为一体、很难分割的，那么两者的互补和相得益彰，就使学生的综合素养提升到一个新的制高点，也将使我们的数学教学上升到一个更高的品位.

2.4 结合贴近学生生活的具体事例强化辩证思维的发展

在学生的实际生活中也存在着大量蕴涵辩证思维的例子，巧妙结合数学内容，利用学生的亲身感悟和体验，辩证思维的科学理念将更加深入学生的心灵.

3.在数学教学中培养学生辩证思维例探

3.1 矛盾是推动事物发展的根本动力

矛盾是推动事物发展的根本动力.“矛”想戳穿“盾”，就须变得越来越锐利；“盾”想防住“矛”，就须变得越来越坚固.“矛”和“盾”之间的争斗推动了“攻、守”双方的不断进步.肝炎原本只有一种“甲肝”，但在人们与甲肝的斗争中，甲肝病毒它要谋求生存，就不断变异，以后就陆续出现了“乙肝、丙肝、丁肝、戊肝、…”.药物与病毒之间的争斗推动了医药事业的发展.

数学中也不乏其例.计算3-5的矛盾，促使负数的诞生；计算3÷5的矛盾，促使分数的诞生；研究方程x2=2解的矛盾，促使无理数的诞生；研究方程x2=-1解的矛盾，促使虚数的诞生；…所以应让学生明白，我们不仅不回避矛盾，而且还要寻找矛盾、发现矛盾，并用创造性的思维解决矛盾，那么我们就会在这个辩证运动的过程中变得越来越聪明、越来越能干.

3.2 矛盾双方的良性转化

矛盾双方在一定条件下是可以实现相互转化的，而转化是非常重要的一种数学思想，是解决数学问题最具威力的一种武器.我们不仅要让学生熟练掌握转化的技能、技巧，而且还要从本质上深刻领会转化中蕴涵的辩证思想，这样才能做到高瞻远瞩、运用自如、得心应手.当然转化有“良性”和“恶性”之分.正常细胞在外界某种刺激源的作用下，产生癌变，这是恶性转化.我们追求的当然是有利于问题解决和能力提高的良性转化.

例1 如图1（1），在侧棱长为2，底面边长为1的正四棱柱ABCD-A1B1C1D1中，P是对角线BD1上的动点，求AP+PC的最小值.

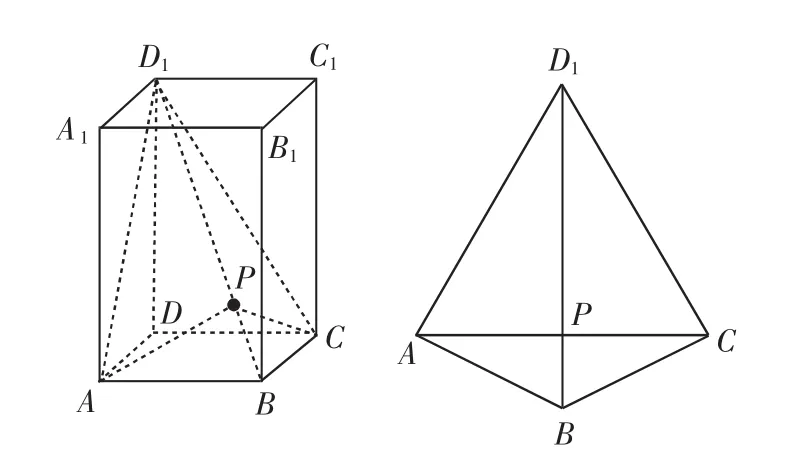
图 1（1） 图 1（2）

分析：在立体几何的学习和问题解决中，有一个突出的矛盾，就是平面的二维空间与立体的三维空间之间的视觉和心理差异.在本题中，求的是AP+PC的最小值，可是AP在平面ABD1内，PC在平面BCD1内，这给题解造成极大的麻烦.可熟稔转化的学生却很快找到突破的方法，将△ABD1与△BCD1所在平面展开为一个平面，得图1（2），则AC之长为所求.

只知道将立体图形展开成平面图形，那是技能；若又知道这是一种普遍规律，那就形成了一种思想；基于此，还知道转化是辩证思想的体现，那就是一种高境界.

3.3 偶然性与必然性

科学中的发明创造看似有一定的偶然性，学生也许认为靠的是某种“运气”，殊不知从偶然性中折射出来的是一种必然性，必然性存在与偶然性之中，这就是哲学的一个基本原理.那种不靠坚实的基础、灵活的思维，靠“撞大运”取胜的心理是不可取的.

苹果从树上掉到地上，是再普通的常见现象，别人见了，无任何反应，但有心的牛顿却从中获得启示发现了万有引力定律.法国著名数学家笛卡儿长期思考用代数方法来研究几何问题.1619年11月10日傍晚，他在朦胧中观察到在墙角结网的蜘蛛，那纵横交错的蛛丝网络引发了他的灵感，那不正是多年来梦寐以求的“坐标系”吗？由此创立了推动世界科技发展的新型数学分支《解析几何》.偶然的发现是长期苦苦思索和孜孜以求的必然结果.

例2 如图2，设抛物线E：x2=2py（p＞0），M为直线y=-2p上任意一点，过M引抛物线E的两条切线，切点分别为A、B.求证：A、M、B三点的横坐标成等差数列.

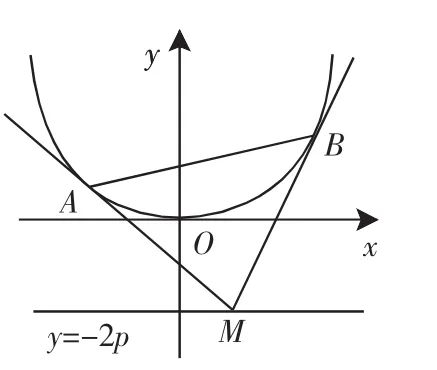
图2

由①②两式，立即知x1、x2是方程x2-2x0x-4p2=0的两根，则x1+x2=2x0.欲证结论成立.

一道颇具难度的高考试题就这样“轻而易举”地被征服了，为闪光的灵感叫好吧！可应看到偶然迸发的灵感背后显示的必然性.要证的是x1+x2=2x0，由此应想到韦达定理，但须有关于x的一个一元二次方程.那么，就会从①②两式中寻求突破.这两式中除字母x1、x2的下标分别为1、2外，其余的结构均相同，由循根找方程的规律，则得x1、x2是方程x2-2x0x-4p2=0的二根，问题解决.从智慧闪光中窥见的是扎实的基础和开阔的思维，是偶然中的必然.

3.4 动中求静变中寓定

“动”和“静”、“变”与“定”也是矛盾对立的事物，是数学研究的极为重要的内容，所以关于定值、定点的数学问题往往成为各级各类数学试卷中的常客.我们不仅要带领学生解决这类问题，更重要的是须使学生发现、利用“动中求静”和“变中寓定”的规律，这对于我们认识宇宙、自然、世界和社会都具有重大的意义.

分析：实数a是非零变量，否则在P点处的切线l为定直线，直线上的点都是定点，探讨此直线过定点将失去任何意义.所以此题妙就妙在不管a的值如何变化，切线l均过定点，即该点的坐标为与a无关的常数.尽管此题证明的难度不大，而启迪意义即在此.

3.5 制约与依赖

制约与依赖也是辩证的对立统一的关系.子女都要受到父母的管束和制约，但又都离不开父母的呵护与抚养.社会中的每一个成员都要受到法律、法规的制约，但这些法律、法规又保护着每个社会成员生命财产的安全.风筝都有一根线牵着，若风筝不想受此制约，脱离了牵线，那它永远也飞不起来.简单的事例中含有深刻的道理.数学中，函数符号f（x）也是如此，如f（x）=2x+1，则当x=1时，函数值f（1）只能由2x+1，即法则“2倍加1”来决定，没有任何“自由”；但欲求的f（1），却又依赖着法则“2倍加1”，否则无从求起.诸如此类现象极其生动地揭示了制约与依赖的辩证关系，学生怎么会“不懂”呢？

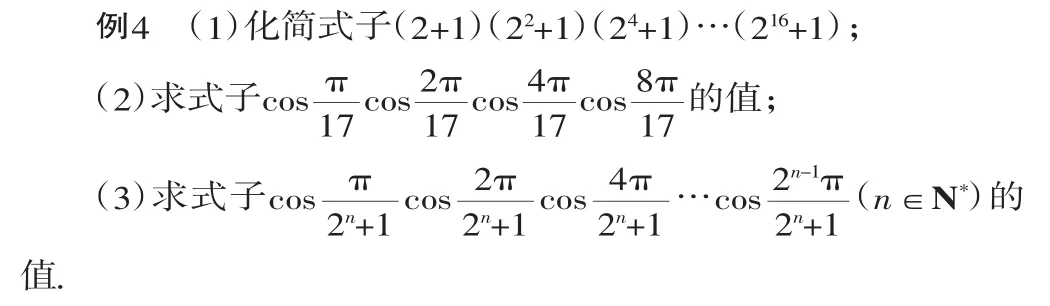
分析：这是一道初、高中衔接的递进式的妙题，（1）中各括号中均为加号，我们不禁想起最简单、最熟悉的公式（a-b）（a+b）=a2-b2，那么在式子前面应添加一个括号，当然是（2-1），这既是后面式子决定了的，也是后面式子给予启示的结果，则得：

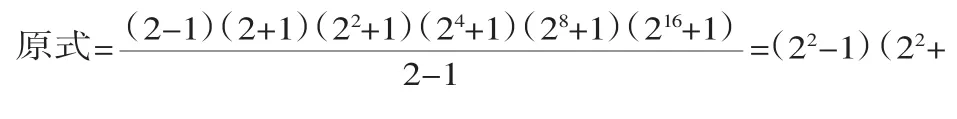
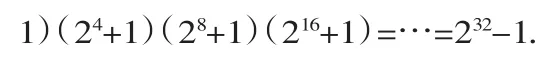
（2）虽然与（1）的结构不一样，但处理的意向却一致的，后面各因式制约了也指明了应添加的因式为于是原式=

积累了经验，解决（3）则不在话下：

此题运用制约与依赖的辩证关系，使题解过程的演绎达到淋漓尽致的境界.

3.6 特殊性与一般性

人们探索、认识、发现、总结社会、世界、自然、宇宙各种事物运动、发展、变化的数量规律，总是从个例到整体、从特殊到一般.一滴水知大海，一滴血知全身，通过一只麻雀的解剖与分析，就可以知道所有麻雀机体的结构与功能，这种理念对于数学的教与学具有巨大的指导意义与实践价值.

如研究指数函数的图像与性质，谁也画不出函数y=ax（a＞0，且a≠1）的图像，只能通过对具体函数等的研究来总结一般指数函数的性质.

解答数学问题，特别是某些选择、填空题，有一种频繁应用的“特殊化”法，但必须逐步引导学生辩证地理解这种方法的本质与操作时应持的科学态度.其一、在解答某些选择、填空题时，特殊化法确实可发挥出巨大的优势；其二、对某些特例研究所获得的结论必须得到一般情况下的证明，才能保证其正确性，否则就犯了“以偏赅全”的错误；其三、对于解答题，虽然“特殊化”不能作为可靠的证明依据，但“特殊化”所获得的结论为一般情形的探索、证明指明了方向，提供了经验，也是“功不可没”的.

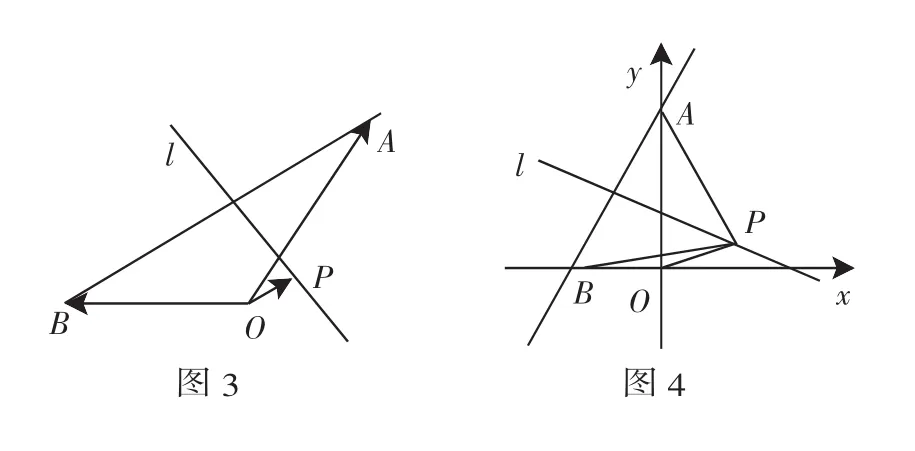
分析：由于是填空题，则可大胆地用特殊化的方法来解：建立如图4所示的坐标系，分别设A（0，3）、B（-2，0）、P（x，y）.由PA=PB，得4x＋6y=5，则

不能以此为满足，将题目改为证明题，条件同上，求证：不论P点在l上的什么位置，p·（a-b）均为定值.

特殊化的方法不能使用了，但其思路与结论仍然具有重要的参考价值与启迪意义，特殊与一般的辩证关系在这里得到了充分的展现.

如图4，建立坐标系，分别设A（acosα，asinα）、B（bcosβ，bsinβ）、P（x，y）（a与b均为定值）.

由PA=PB，得2axcosα-2bxcosβ+2aysinα-2bysinβ=a2-b2.

小、大两题的联袂出现与解决，可认为是在辩证法指导下进行数学科研的一次有意义的实践活动，对于学生全方位的成长与综合素质的提高具有积极的意义，并产生深远的影响.

3.7 量变到质变

“量变到质变”是辩证法中的一个非常重要的基本原理，与此相关的数学内容不胜枚举，初中学生非常熟悉一元二次方程实数根个数的判断，以及点与圆、直线与圆的位置的判断，这些都是讲解“量变到质变”这一基本原理的知识基础，但那时学生的理解必然是十分粗浅的，在高中阶段有机结合教学内容进行这方面的讲解就可以从根本上加深学生对这一基本原理的理解.

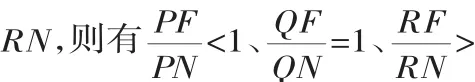
例6 如图5，设平面内的一条定直线l以及l外的一个定点F，平面内的动点P、Q、R到直线l的距离分别为PN、QN、1三种情形.若设这些比值为e，并称为离心率，则当e∈（0，1）时，动点的轨迹是椭圆；当e=1时，动点的轨迹“脱胎”为抛物线；当e∈（1，＋∞）时，动点的轨迹又“羽化”为双曲线.

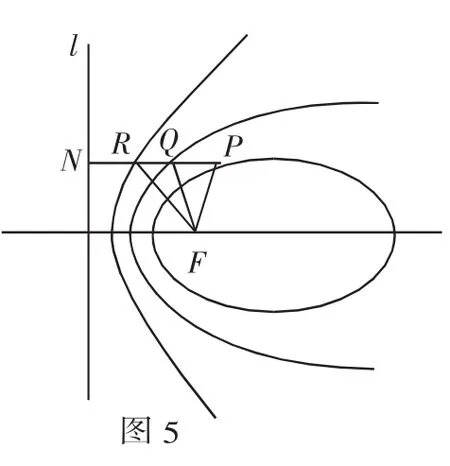
客观事实极其深刻地揭示了“数量的积累变化达到，或越过一个关键值时，事物就会发生质的变化”这一本质规律.

结合生活中的许多事例，“量变到质变”这一基本原理还可以给予我们诸多启示.

3.8 抓住主要矛盾

古诗云：“射人先射马，擒贼先擒王”；军事指挥员说：“先解决外围，最后集中优势兵力攻坚”；农夫说：“打蛇要打七寸”；牧童说：“牵牛要牵牛鼻子”，雅俗共赏的语言说明的是同一个道理，即解决问题时要抓住主要矛盾.面对矛盾错综复杂的一件事情，理清各种矛盾的关系，分清主次，“牵住牛鼻子”，就大大降低了难度，使问题迎刃而解.

1.恩格斯.自然辩证法.北京：人民出版社，1971.

2.中华人民共和国教育部制定.普通高中数学课程标准（实验）.北京：人民教育出版社，2003，4.