浅析指数函数的常见考点
☉河南省罗山高级中学 杨 希
指数函数是我们学习的重要基本函数之一,蕴涵了丰富的函数的内容和函数思想,也是高考中的“常客”.接下来笔者就指数函数的常见的考点略作小结,供读者参考.
一、指数函数的主要内容
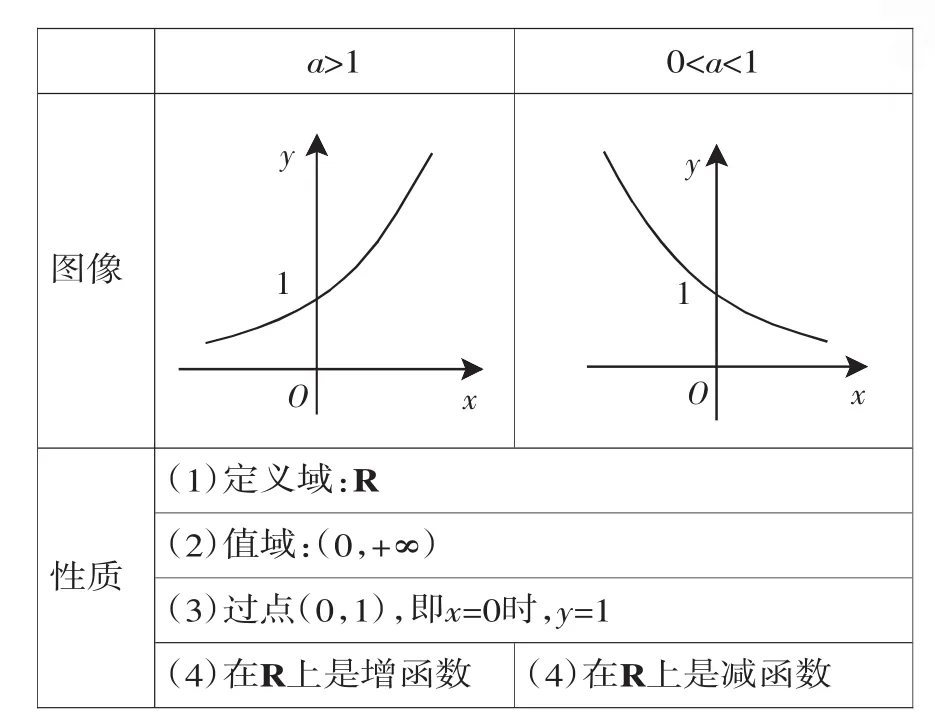
a>1 0 定义是学习新知识的基础,深刻理解定义对整节内容的学习至关重要. 例1若函数f(x)=(a2-3a+3)·ax是指数函数,则a=______. “数形结合”是高中数学的重要数学思想之一,能直观的反映出问题的本质.掌握指数函数的图像特征和性质,结合图像变换法则画出图像,便可使一些复杂的问题更直观、更简捷. 例2已知f(x)=ax(a>1),g(x)=bx(b>1),当f(x1)=g(x2)=2时,有x1>x2,则a、b的大小关系是______. 分析:指数函数图像具备如下性质:在第一象限图像离x轴越远,函数的底越大.具体证明(如图1),取x=1,则有c 解:根据题设,画出图像,如图2,利用指数函数的性质,则有a 图1图2 “单调性”是函数的重要性质之一.构造指数函数模型,利用单调性比大小、解不等式、求值域等是常考题型. 由f(m)>f(n),得m “函数与方程思想”是数学的重要思想之一.函数是方程与不等式的“中介”,三者既有区别,又联系紧密,相互转化. 例4 若关于x的方程4x+1-m4x-m-3=0有正根,求m的取值范围. 分析:这是含有参数的指数方程,根据指数函数的性质、方程与函数相互转换等知识,有以下几种思路. 解法1:利用指数函数的值域转化为关于m的不等式. 解法2:把原方程换元转化为关于4x的一次函数来研究. 设4x=t.由x>0,得t>1. 原方程变形为(4-m)t-m-3=0.(1) 设f(t)=(4-m)t-m-3(t>1),原方程有正根,等价于方程⑴在区间(1,+∞)内有实根,则只要函数f(t)在区间(1,+∞)内的图像与横轴相交. “分类讨论”一直是高考重点考查的内容之一.常见的分类情形有:按数的特性分类;按字母的取值范围分类;按事件的可能情况分类;按图形的位置特征分类等.指数函数涉及的讨论主要是底“a”的范围的讨论. 例5若函数f(x)=ax-x-a(a>0,a≠1)有两个零点,则实数a的取值范围是______. 分析:设函数y=ax(a>0)且a≠1)和函数y=x+a,则函数f(x)=ax-x-a(a>0,a≠1)有两个零点,就是函数y=ax(a>0且a=1)与函数y=x+a有两个交点.由图像可知当0 例6若函数f(x)=ax(a>0,a≠1)在区间[1,2]上的最大值是最小值的3倍,则a=________. 分析:由于底a大小不定,则函数的单调性不定,故需要讨论. 解:①当a>1时,f(x)=ax(a>0,a≠1)单调递增,则a2=3a⇒a=3或a=0(舍去). ②当0二、常见考点例析
考点一:指数函数的定义考查
考点二:指数函数的图像考查
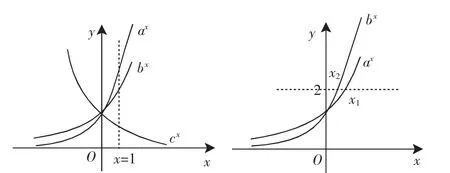
考点三:指数函数的单调性的考查
考点四:函数与方程思想的考查

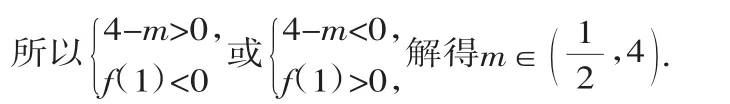
考点五:分类讨论思想的考查

