对圆锥曲线焦点三角形角平分线的一个性质的再推广

☉安徽省肥东第一中学 周自浩

对圆锥曲线焦点三角形角平分线的一个性质的再推广

☉安徽省肥东第一中学 周自浩

圆锥曲线焦点三角形角平分线的性质在各种试题中常常出现，引起大家的关注．本文结合近期几位同仁的工作，对其中内角平分线与切线的关系做了整理，并推广到所有圆锥曲线中．

一、推广后的三个定理及其证明

问题 （2011年北大保送生考试题）点P为双曲线上任一点，PQ为双曲线在点P处的切线，F1、F2为双曲线的焦点.求证：PQ平分∠F1PF2.证明见文［1］.

此结论可以表述为：

定理1 点P为双曲线上任一点，F1、F2为双曲线的两焦点，则双曲线在P点处的切线与∠F1PF2的平分线重合.

事实上，此种切线与角平分线的类似关系可以推广到所有圆锥曲线中.

定理2 点P为椭圆上任一点，F1、F2为椭圆的两焦点，则椭圆在P点处的切线与∠F1PF2的平分线垂直.

对于定理1，文［2］给出了一个与文［1］不同的证法.事实上，文［2］是先考虑定理2，然后推广得到定理1的.文［1］、文［2］都没有给出定理2的具体证法，现补充一种证法如下.

图1

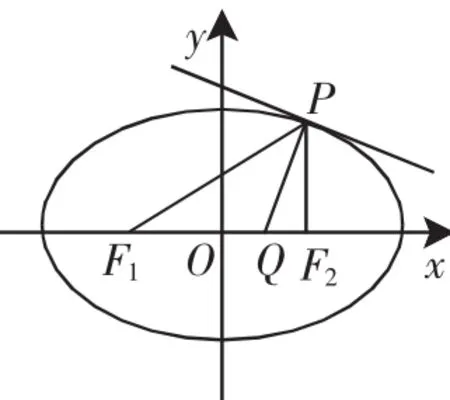
图2

由夹角公式可得：

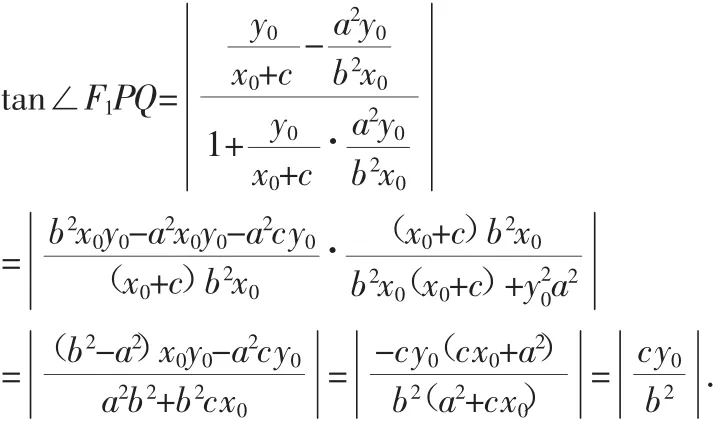
即有tan∠F1PQ=tan∠F2PQ，知直线PQ是∠F1PF2的平分线．

定理3 点P为抛物线上任一点，F为抛物线的焦点，过P作抛物线的准线的垂线，垂足为P′，则抛物线在点P处的切线与∠FPP′的平分线重合.

图3

即有tan∠QPP′=tan∠FPQ，所以PQ为∠FPP′的平分线.

二、推广后定理的统一物理意义

这三幅图像反映出在圆锥曲线的光学性质中的镜面就是我们数学中的切线．

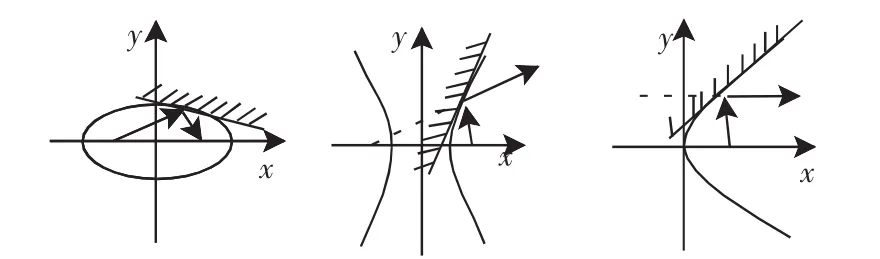
图4

三、定理的应用

例2 求证：直线l过抛物线y2=2px（p＞0）的焦点F，交抛物线于A、B两点，则抛物线在A、B两点处的切线互相垂直.

图5

证明：分别过A、B两点作抛物线准线的垂线，垂足分别为C、D两点，由定理3知道抛物线在A、B两点处的切线分别平分∠CAB、∠DBA，而∠CAB与∠DBA互补，所以抛物线在A、B两点处的切线所成角为90°，即互相垂直.

（1）求椭圆E的方程；

（2）求∠F1AF2的角平分线所在直线l的方程；

分析：（2）易得椭圆在点A处的切线斜率，再由定理2得直线l的斜率.

1.范瑞喜.2011年北大保送生考试数学试题赏析［J］.数学通讯，2011（4）.

2.蔡润芳.圆锥曲线焦点三角形顶角平分线的性质探究［J］.数学通讯，2012（2）.

3.玉邴图.由一道高考题引发的研究［J］.数学教学，2012（1）.