数列不等式证明方法归类分析

☉甘肃省渭源县第一中学 曹平原（特级教师）

数列不等式证明方法归类分析

☉甘肃省渭源县第一中学 曹平原（特级教师）

*本文是甘肃省2012年省级规划课题《信息技术环境下的高中数学教学设计的研究》成果之一.

数列不等式是含有数列的通项an或前n项和Sn的不等式．在近年来的全国各地高考数学试题中，数列不等式证明问题多次出现，已经成为全国高考数学命题所特别关注的焦点．

数列不等式处于数列与不等式知识的交汇点，通常呈现递推形式．数列不等式的证明问题，所涉及的知识点较多，是综合性较强、灵活性较高、难度较大的数学证明问题．

由于数列不等式与自然数有关，所以在证明数列不等式的过程中，最容易联想到数学归纳法．虽然利用数学归纳法可以证明一些数列不等式，但是在更多的情况下，用数学归纳法证明数列不等式并不顺利．解决数列不等式证明问题，需要转换思维方式，从多角度、多方位去思考，需要利用各种不同的方法．其中放缩法最为重要，应当把放缩法渗透在证明数列不等式的各个环节中．只有把各种方法巧妙地结合起来，才能够较好地解决数列不等式的证明问题．下面对2012年全国高考数学试题中的数列不等式的证明问题，做以归类总结和分析点评，供大家参考.

一、用数学归纳法证明数列不等式

例1 （全国Ⅱ卷第22题）函数f（x）=x2－2x－3，定义数列{xn}如下：x1=2，xn+1是过两点P（4，5）、Qn（xn，f（xn））的直线PQn与x轴交点的横坐标.

（Ⅰ）证明：2≤xn＜xn+1＜3；

（Ⅱ）求数列{xn}的通项公式.

解：（Ⅰ）用数学归纳法证明：2≤xn＜xn+1＜3.

所以2≤xk+1＜xk+2＜3，即当n=k+1时结论成立.

由（1）、（2）知对于任意的正整数n，2≤xn＜xn+1＜3.

二、用放缩法证明数列不等式

例2 （广东A卷第19题）设数列{an}的前n项和为Sn，满足2Sn=an+1－2n+1+1，n∈N*，且a1、a2+5、a3成等差数列.

（Ⅰ）求a1的值；

三、利用等价关系证明数列不等式

例3 （安徽理第21题）数列{xn}满足：

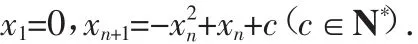
（Ⅰ）证明：数列{xn}是单调递减数列的充分必要条件是c＜0；

（Ⅱ）求c的取值范围，使数列{xn}是单调递增数列.

四、利用函数单调性证明数列不等式

例4 （天津理第20题）已知函数f（x）=x－ln（x+a）的最小值为0，其中a＞0.

（Ⅰ）求a的值；

（Ⅱ）若对任意x∈［0，+∞）有f（x）≤kx2成立，求实数k的最小值；

五、利用分类讨论和分析法证明数列不等式

例5 （重庆理第21题）设数列{an}的前n项和Sn满足Sn+1=a2Sn+a1，其中a2≠0.

（I）求证：{an}是首项为1的等比数列；

六、利用化归法和基本定理证明数列不等式

在（Ⅱ）和（Ⅲ）的解题过程中，都是先把要证明的数列不等式转化归结为比较简单的不等式，然后结合二项式定理、均值定理等有关数学知识，利用放缩法进行证明.