高三数学一轮复习不可忽视的几个环节
☉江苏省海安县立发中学 陈士芳
高三数学一轮复习不可忽视的几个环节
☉江苏省海安县立发中学 陈士芳
高三数学一轮复习在整个高考复习中是必不可少的,也是至关重要的.有人认为一轮复习就是简单的回顾知识点,然后进行大量的题目训练,殊不知,这样一不小心就掉进题海战.现在的高考侧重考查学生的基本知识、基本技能和基本方法,其中对能力的考查尤为重要,想要在高考中碰陈题就如大海捞针,所以我们要避开这种既加重学生的学习负担,又收效甚微的题海战术,这就要求高三一轮复习过程中,我们要从各个环节入手,全面复习.让我们的学生经过一轮复习后对概念的理解更全面、更深刻,同时拥有类题辨析能力,对一些错题能够轻松地防御和击破.在各个环节实施过程中,让学生的解题能力得到有效的提高,最终使他们在高考中立于不败之地.
一、概念的回顾
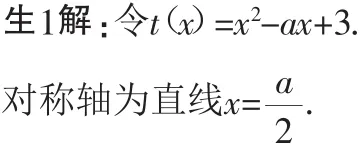
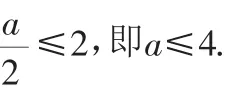
点评:此生在解题时只注意到单调性概念中提到的对于∀x1、x2∈[2,+∞),且x1<x2,总有f(x1)<f(x2)成立这个条件,但忽视函数单调性的大前提,[2,+∞)⊂D,D为函数的定义域.

点评:此生在解题时误认为在(-∞,1)和[1,+∞)上单调递减等价于在R上单调递减,而概念的条件必须满足对∀x1、x2∈R且x1<x2总有f(x1)<f(x2)成立,教师可以借助图像帮助学生理解概念中的“任意”的条件.

可见,对概念不仅仅是记住,更重要的是理解和运用.我们在给学生复习概念时,一方面复述其内容,强调关键语句,另一方面要借助于例题帮助学生理解概念的实质含义,引导学生正确地使用.
二、习题课的引申
习题课上老师给出的例题要求是经过精心准备的典型性的题目,这些例题是教师与同行通过多年的教学经验积累的,对学生的学习要有指导作用.但在讲题时我们不能仅仅满足于就题论题解出这道题的结果.一方面,对于一道试题我们要引导学生从不同的角度审视,采用不同的解题方法,通过一题多解的方法的训练培养学生思维的灵活性和广阔性.另一方面,我们可以将例题进行变式,变成形同质异或形异质同的题目,引导学生从“变”中寻求“不变”的本质,通过一题多变的方法的训练培养学生的化归能力.
案例3 已知在△ABC中,AB=2,AC2+BC2=10,求△ABC面积的最大值.
两位学生给出了不同的解法.
解法1:令△ABC中A、B、C所对的边分别为a、b、c.

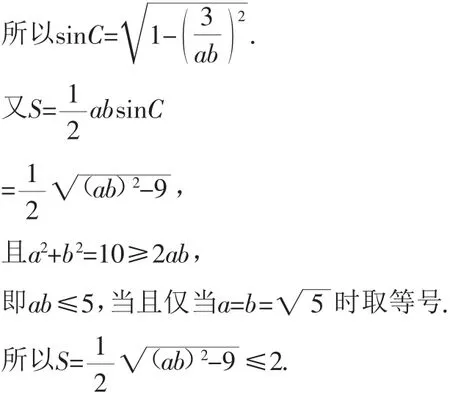
故△ABC的面积的最大值为2.
解法2:以A、B所在的直线作为x轴,以AB的中点O为原点建立平面直角坐标系.
则A(-1,0),B(1,0).令C(x,y).
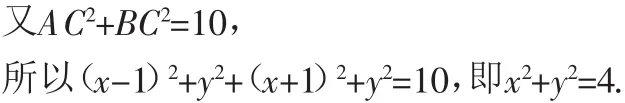
所以C点的轨迹是以O为圆心,2为半径的圆,除去点(2,0)和点(-2,0).
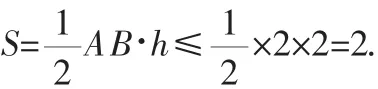
故△ABC面积的最大值为2.
点评:两位学生从不同的角度对这一题进行分析、求解.方法1是从余弦定理入手,借助不等式求出面积的最大值;方法2是从C点的轨迹入手,借助圆的图像、性质求出三角形面积的最大值.对于两种方法我们都要给予肯定,鼓励学生从不同的角度审题,促使他们一题多解,从而拓宽学生思维的广阔性.
课上我们还可以将此题变式.
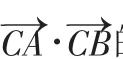
这些变式形式上虽然不同,但本质仍然有相同的特征.在复习时教师可以时常对这类题目进行训练,归纳出通性通法,学生就可以实现解一题等于解一类题的目的.又比如:
(1)已知函数f(x)=lg(ax2+2x+1),若函数f(x)的定义域为R,求实数a的取值范围.
(2)已知函数f(x)=lg(ax2+2x+1),若函数f(x)的值域为R,求实数a的取值范围.
这两个问题看似相同,但本质上是完全不相同的,学生容易混淆,所以教师在复习时要引导学生观察、类比、推敲、归纳它们的区别和联系,挖掘题目的本质,寻求解题的方法,从而实现在变化中求进步,在进步中求变通的目标.
三、讲评课的示错、纠错
进入高三复习阶段,试题的练习远远多于高一、高二,讲评课的课时在总课时所占的比例甚至高于三分之二,这就决定了讲评课的效率深深地影响着学生的复习收益.学生在练习时出错是正常的,教师要接受、包容并帮助学生分析出错的原因,而不是一味地指责学生“不认真”“粗心大意”.笔者在多年的教学中发现,不同的时空,不同的学生常常发生相同的错误的现象,这就表明错误也具有共性,我们教师要充分利用学生出错的资源,寻求出错的原由,挖掘题目的本质,提高讲评课的效率,这样才能取得事半功倍的效果.
案例4 已知直线l过点P(1,2),且在两坐标轴上的截距相等,求直线l的方程.

点评:学生能从截距式入手,但对截距式的使用条件理解不全面,忽视了直线过原点即截距均为零的情况.
生乙错解:由已知可设直线方程为y-2=k(x-1).

又因为直线在两坐标轴上的截距相等,

点评:学生对截距的概念有错误的认识,将截距与距离混为一谈,认为截距是非负的.
这两种错误都体现了学生对截距的概念及截距式方程理解的偏差,上课用投影仪展示出来,既可帮助学生找到错误的源头,对知识进行重新的认识,又可培养学生类比、辨别能力,进而提高学生突破思维障碍的能力.
四、易错题的整理
学生在做题目时都会出现一些错误,对于这些错误,在老师讲评之后学生不能仅仅满足于订正就完事了.因为我们经常发现这种错误以前发生过,之后学生也订正过,但过一段时间又犯同样的错误,这就说明问题仍然存在,学生需要花费更多的精力去克服困难,解决问题.
一方面,要求学生将当天出现的错题用红笔订正在试题旁并说明错误的原因,同时要求学生都必须备有“错题笔记本”,将易错题(仅仅是题目)摘抄,两个星期或更长的时间之后再订正,若订正对了,证明有进步,这类题得到解决;若错了,说明上次订正不到位,再次重复以上步骤,直到订正对为止.另一方面,要求老师对学生的易错题进行分类、整理、变式、延伸,将这些题以试卷的形式呈现,检测学生纠错的情况和举一反三的能力.在老师和学生的共同努力下,学生的易错题将会越来越少,知识点越来越清晰,各方面的能力越来越得到提高.
五、反思的写作
高三数学由于内容多,教师往往舍不得花时间让学生进行反思.学习过程得不到反思,学生就会经常重复着前面的错误,教师为此非常苦恼.笔者认为反思是教学中必不可少的环节,反思可以促进学生对概念有更深刻的理解,对解题方法有更全面的体会.笔者认为数学反思写作的形式非常灵活,字数、内容、格式均不受限制,只要求学生写出自己当日数学学习的真实想法.
下面笔者呈现两位学生的反思.
生A:对概念学习的反思:
今天学习了椭圆的定义,我用代数式表示.

n不是最高次数,而是表示项数.
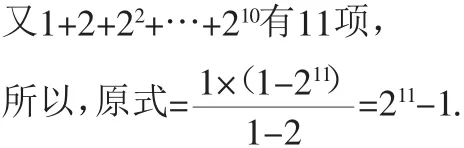
让学生写反思,一方面可以完善学生对知识的理解,拓宽学生的思维方式,提高解题能力,另一方面,老师通过阅读学生的反思了解学生的学习情况,及时调整教学计划,同时促进师生之间的交流.
高三数学一轮复习是一项巨大的工程,以上的各个环节都要认真、细致地实施.经过一轮复习,我们的学生不仅能回顾基本知识,还能将知识不断深化,理清知识之间的关系,逐步形成结构体系,掌握解题的基本方法,最终实现全面提高解题能力的目标.

