好题共欣赏 基础不能忘
☉江西省安远县第一中学 郑方相(特级教师)
好题共欣赏 基础不能忘
☉江西省安远县第一中学 郑方相(特级教师)
编者的话:
该文从多角度入手,应用不同的三角公式对2012年高考江西卷理科第17题进行求解,虽然三角试题为基础题,但为考生要全做对的题目.数学中对问题从多方向进行分析,能够融会三角知识,提高熟悉程度和正确性.对教学有一定的参考性.
2012年高考江西卷理科第17题是一道三角题,该题容易入手,从不同的角度出发均能轻松地加以解决,很好地体现了“考查基础知识的同时,注重考查能力”的命题原则,有效地考查了考生的数学基础知识和基本技能.以下是该题的多种不同解法.







图1
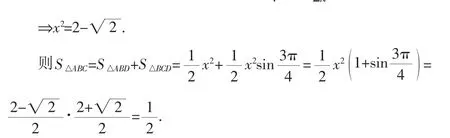
以上不同的证法(解法)中,主要涉及两角和与差的正弦公式、倍(半)角公式、正(余)弦定理、三角形中的诱导公式、积化和差、和差化积公式、三角形面积公式的简单运用,其中除积化和差、和差化积、半角公式在《考试说明》中不要求记忆以外,其他的都要求熟练掌握,而本题的解答完全可以不用积化和差、和差化积和半角公式.由此可见,只要我们在教学中紧扣教材,夯实基础,牢牢把握通性通法,适当地进行一些基本技能的训练,考生便能顺利地拿下高考中的三角题.
概念是对某知识的描述,这种描述包含了此知识的特征、特性、使用的条件等,对概念的深刻理解是一切数学活动的基础.对概念的回顾,笔者认为不仅是陈述概念的内容或是指出关键字,而且是对概念的正确的理解和灵活的运用.我们只有对概念充分理解,才能深入了解数学的本质,对一些改头换面的题目才能迎刃而解.因此在一轮复习中对概念的回顾不能草草了事.
笔者在高三复习函数的单调性概念时,发现存在学生基本上能回忆出概念的内容,但在使用概念解题时却对概念理解不透彻的问题.
案例1 已知函数f(x)=lg(x2-ax+3)在[2,+∞)上单调递增,求a的取值范围.

