陈题巧改编、旧瓶装新酒

☉浙江省绍兴县柯桥中学 张惠民（特级教师）

陈题巧改编、旧瓶装新酒

☉浙江省绍兴县柯桥中学 张惠民（特级教师）

高考复习中常常出现这种现象：重复昨天的故事，教师讲课少了一份激情，学生听课感觉枯燥乏味.若“求新、求异、求难”，复习方向是否会偏离？是否会丢掉根本？题海茫茫，何处是尽头？

笔者认为以“常规题型”为载体，变换问题情景、揭示问题本源、适度包装改造不失为解决“旧与新”、“易与难”、“传统与创新”几对矛盾的有效办法.

下面是高考复习中一个课例的构思节选，供读者借鉴.

一、中规中矩“点差法”

评注：点差法是解析几何中一种常规的但又非常重要的解题方法，用于此题使证明过程简洁流畅.但如果就这样简单地处理此题，对学生而言，又是“重复了昨天的故事”，并有一种“被做题”的感受.

二、合情推理“类比法”

能否在此题中添加一些使学生感兴趣的元素呢？联想平面几何中的“垂径定理”：圆心与弦的中点的连线垂直于该弦.在两条直线斜率均存在的情况下，垂直则斜率之积为-1.由此形成以下从圆到椭圆的合情推理.

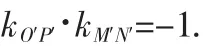
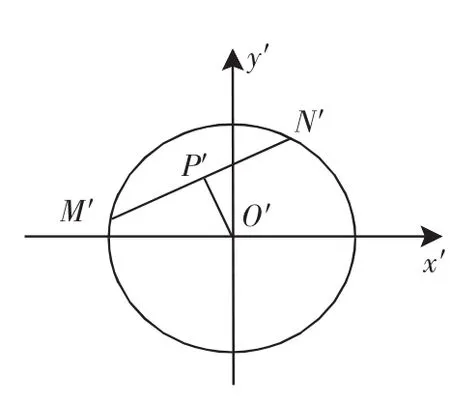
图1

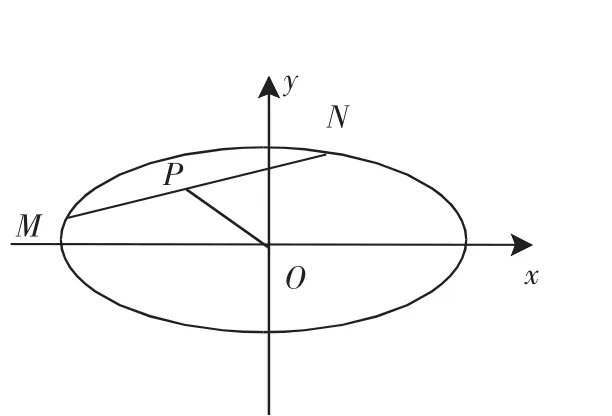
图2

评注：问题的起点是圆，结论的指向为椭圆，这种合情推理的问题情景，学生感到自然而亲切.问题以探究的形式呈现，更容易激发学生的学习热情.

三、登高望远真相大白

以上的类比是否有更深层次的知识背景为支撑呢？我们知道直线在压缩变换后仍为直线.

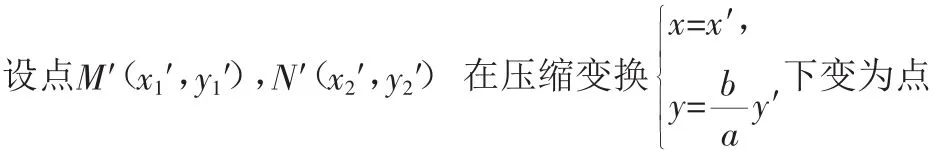
四、适度包装编新题

俗话说“铁打的营盘，流水的兵”.高考中不变的是知识，变化的是情景的呈现形式、问题的结构方式.这就要求我们在高考复习中，寄予常规又突破常规，陈题巧改编、旧瓶装新酒.

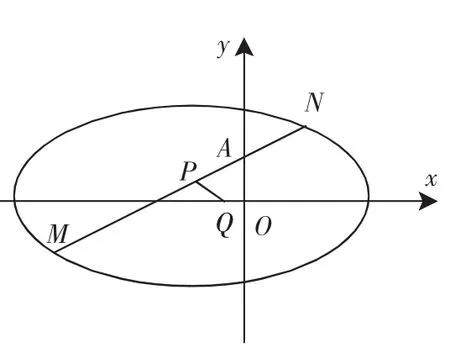
图3

分析：设M（x1，y1），N（x2，y2），P（x，y），直线l的方程为：y－1=k（x+1），即y=kx+k+1.

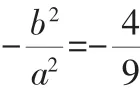
五、异曲同工再设计

数学学习是一个循序渐进的过程，学生构建知识网络需要一定的载体来实现.为此笔者又设计了以下两个问题供学生课后思考.

设计思路：以结论“直径上的圆周角为直角”为雏形进行问题设计.

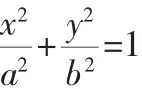
对上述结论进行特殊的、逆向的设计，形成了本命题.其中设置A、B在x轴上，目的是为了减小探究的难度.

设计思路：以结论“直径必过圆心”为雏形进行问题设计.