初探培养初中生数学解题能力的策略

☉江苏省盐城市明达中学 徐 芬

初探培养初中生数学解题能力的策略

☉江苏省盐城市明达中学 徐 芬

新课程要求有效的数学学习活动，不能单纯地依赖模仿与记忆.动手实践、自主探索与合作交流是学生学习数学的重要方式.教师应激发学生的学习积极性，向学生提供充分从事数学活动的机会，帮助他们在自主探索与合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学活动经验.本文谈谈新课程背景下培养初中生数学解题能力策略.

一、重视一题多解，开阔解题思路

一题多解是从不同的视角、不同的方位审视分析同一问题中的数量、位置关系，用不同解法求得相同结果的思维过程.通过探求同一问题的不同解法，可以引出相关的多个知识点和解题方案，有助于培养学生的洞察力和思维的变通性、独创性，从而培养学生的解题能力.

例如 ▱ABCD的对角线相交于点O，E、F分别是OB、OD的中点.四边形AECF为平行四边形吗？为什么？（教学苏科版八上《数学》115页8）

四边形AECF为平行四边形.

证法一：说它的两组对边分别平行的四边形是平行四边形；

证明二：说它的一组对边平行且相等的四边形是平行四边形；

证法三：说它的两组对边分别相等的四边形是平行四边形；

证法四：说它的对角线互相平分的四边形是平行四边形.

通过对本题多种证法的探究，不仅复习了平行四边形的判定方法，而且培养了学生善于从不同角度思考问题的习惯，提高学生的学习积极性开阔解题思路.

二、重视一题多用，锤炼解题能力

初中数学教师的主要职责是不仅要传授知识，而且要引导学生自己去求得知识.初中数学教学不能光灌输，还要加强解题方法指导.那种尽管表面看起来形式并不一致甚至差别很大的问题，它们的求解思路、解题步骤乃至最后结果却非常相似，甚至完全相同，对它们要通过一题多用锤炼学生的解题能力.

例如 已知一条直线上有n个点，则这条直线上共有多少条线段？

变式1：初一八班有50个同学，如果在一次游戏中每两人互握一次手，共需握手多少次？

变式2：甲、乙两个站点之间有5个停靠站，每两个站点之间需准备一种车票，则共需准备多少种车票？

变式3：平面内点O在直线l外，在直线l上取8个点，它们与点O可以组成多少个三角形？

变式4：在9名班干部中选出两名优秀班干部，则甲和乙同时当选的概率是多少？

变式5：n边形共有多少条对角线？

通过以上变式问题训练，我们可以通过建立同一数学模型来解决，不仅培养了学生归纳整理的能力，而且深化了学生建模思想和应用数学模型的意识，锤炼了学生的解题能力.

三、重视一题多变，提升解题能力

通过对习题的题设或结论进行变换，对同一个问题从多个角度来研究，这种训练可以增强学生解题的应变能力，培养思维的广阔性和深刻性，从而培养创新思维的品质，提升解题能力.

例如 我教学苏科版七年级下册《数学》P106的习题：“如图1，MS⊥PS，MN⊥SN，PQ⊥SN垂足分别为S、N、Q，且MS=PS.试说明△MNS与△SQP全等的理由”.这时采用了下面几道变式题训练提升学生解题能力.

变式1：如图2，把一个三角板（AB=BC，∠ABC=90°）放入一个“U”形槽中，使三角板的三个顶点A、B、C分别在槽的两壁及底边上滑动，已知∠D=∠E=90°，在滑动过程中你发现线段AD与BE有什么关系？试说明你的结论.

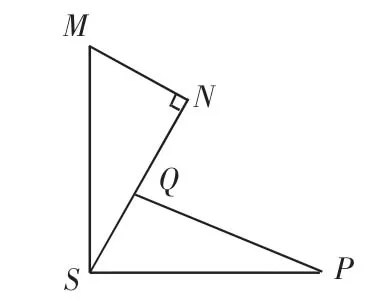
图1

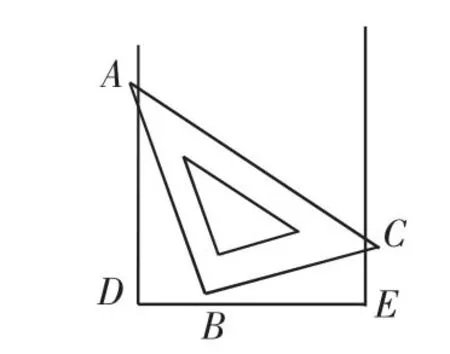
图2

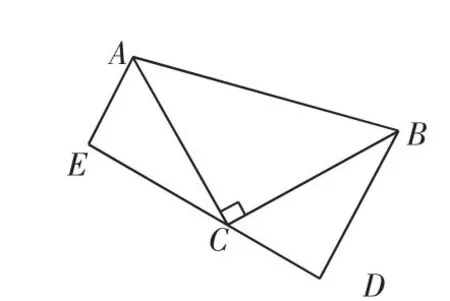
图3

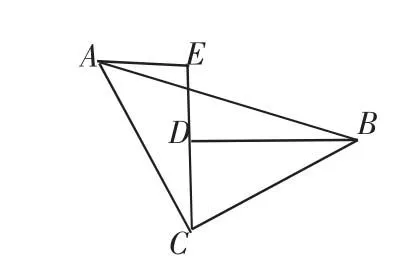
图4

变式2： 如图3和图4，∠ACB＝90°，AC＝BC，BD⊥DE，AE⊥DE，垂足分别为D、E．

（1）图3中，①△ACE与△CBD全等吗？为什么？②若AE＝a，BD＝b，计算△ACB的面积．

（2）图4中，若AE＝a，BD＝b（b＞a），计算梯形ADBE的面积．

变式3：已知：CD经过∠BCA顶点C的一条直线，CA=CB．E，F分别是直线CD上两点，且∠BEC=∠CFA=∠α．

（1）若直线CD经过∠BCA的内部，且E，F在射线CD上，请解决下面两个问题：

① 如图5，若∠BCA=90°，∠α=90°，

则BE____CF；EF____|BE－AF|（填“＞”，“＜”或“=”）.

② 如图6，若0°＜∠BCA＜180°，请添加一个关于∠α与∠BCA关系的条件，使①中的两个结论仍然成立，并证明两个结论成立．

（2）如图7，若直线CD经过∠BCA的外部，∠α=∠BCA，请提出EF，BE，AF三条线段数量关系的合理猜想（不要求证明）．

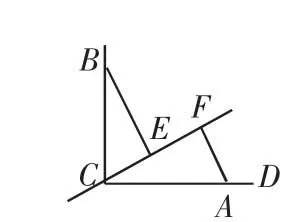
图5

图6

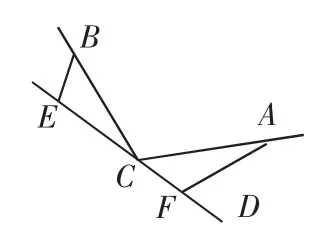
图7

变式4：如图8，△ABC中，∠ACB＝90°，AC＝6，BC＝8．点P从A点出发沿AC－B路径向终点运动，终点为B点；点Q从B点出发沿B－C－A路径向终点运动，终点为A点．点P和Q分别以1和3的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F．问：点P运动多少时间时，△PEC与△QFC全等？请说明理由．

通过对以上问题的分析讨论，学生能够从中发现一题多变，启发学生从不同的角度去思考.这样既能梳理知识、巩固知识，又能开拓了思维的广度，促进了思维的发展，提升了学生的解题能力.

总之，初中数学教学中，只要我们重视一题多解，开阔解题思路，重视一题多用，锤炼解题能力，重视一题多变，提升解题能力，就一定能够培养初中生的数学解题能力.

图8