圆锥曲线统一定义的解题功能

2012-08-27 02:41湖南省永州市第二中学邓艮平

☉湖南省永州市第二中学邓艮平

圆锥曲线是平面解析几何的重要曲线，其性质是历年高考考查的重点.本文举例说明圆锥曲线的统一定义的解题功能，供同学们参考.

例2 （2010年全国I卷理科21题的推广）已知圆锥曲线C的一个焦点为F，与F相对应的准线交F所在轴于点K，过K的直线l与C交于A、B两点，点A关于焦点所在轴的对称点为D，则点F在直线BD上.

证明：（1）当A、B位于同弧时，如图2所示，设BD与焦点所在轴交于点F′（不同于点F）.由题意知点K为准线与x轴的交点，过B、D分别作准线的垂线，垂足为M、N.因为点A关于焦点所在轴的对称点为D，所以∠BKF=∠DKF.

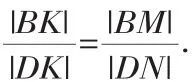
综合（1）（2）知，点F在直线BD上.

例3 过圆锥曲线的一个焦点F作一条同弧弦AB，过B作BC平行于焦点所在的轴，交相应准线l于点C，l与焦点所在的轴交于点E，则直线AC经过线段EF的中点.

EM∥AD.

故直线AC经过线段EF的中点.

猜你喜欢

中学数学杂志的其它文章: 圆锥曲线切点弦所在直线方程; 函数y=Asin（ωx+φ）习题课案例分析; 突破抽象函数问题的十一招; 境由心生; 流程图（程序框图）高考题型例解; 新课程下的立体几何教学要做好“三实”