突破抽象函数问题的 十一招

☉四川省资阳市外国语实验学校 蔡勇全

抽象函数是指既没有给出具体的函数解析式，又没有用列表或图像的方法表示出来，只是给出一些特殊条件（如函数的定义域、函数图像经过的特殊点、解析递推式、部分图像特征等）的函数.此类函数问题具有构思新颖、概念抽象、隐蔽性强、解法灵活多变等特点，是考查学生对函数性质的代数推理和论证能力、对数学语言的阅读理解和转译能力以及学生的抽象思维能力的有效载体，因而历年来备受高考命题者的青睐.本文结合实例介绍突破抽象函数问题的十一种策略，供大家参考.

一、特型探路

抽象函数问题的设计或编拟，常以某个基本函数为特型.在解题前，若能从所研究的抽象函数问题的条件入手，寻找其特型函数，通过分析、研究其图像或性质，找出问题的解法或证法，则可使解题少走许多弯路.

分析：由条件（3）知可用y=logax作为特型函数，又由条件（1）知0＜a＜1，从而y=logax在（0，+∞）上为减函数，故本题可先证f（x）在（0，+∞）上为减函数，以此作为解题突破口.

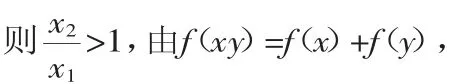
由f（1）=f（1）+f（1），得f（1）=0.

f（x）+f（5－x）≥－2=2f（2）=f（4），则x＞0，5－x＞0，且x（5－x）≤4，解得0＜x≤1或4≤x＜5.

评注：由题中所给抽象函数的结构特征，联想学过的具有相同或相似结构的“特型函数”，并由“特型函数”的相关性质，预测、猜想抽象函数可能具有的性质常常是解决抽象函数问题的突破口，但一定要注意不能直接用“特型函数”替代抽象函数，那样将犯用特殊代替一般的错误（解答客观题还是允许的）.

二、构造函数

抽象函数问题中常常会出现下面的情形：若函数f（x）、g（x）在区间（a，b）上均有意义，且对于任意x∈（a，b），f（x）≥g（x）恒成立.解决这类问题的较好思路是通过构造差函数并结合导数的有关知识.

例2设函数f（x）、g（x）在区间［a，b］上可导，且f′（x）＞g′（x），则当a＜x＜b时，有（ ）.

A.f（x）＞g（x）B.f（x）＜g（x）

C.（fx）+g（a）＜g（x）+（fa）D.（fx）+g（b）＜g（x）+（fb）

解析：构造函数F（x）=（fx）－g（x），由函数（fx）、g（x）在区间［a，b］上可导，得函数F（x）=f（x）－g（x）在区间［a，b］上可导.又f′（x）＞g（′x），则F（′x）=f（′x）－g（′x）＞0在区间［a，b］上恒成立，即函数F（x）=（fx）－g（x）在区间［a，b］上单调递增，故对任意x∈（a，b）恒有F（x）＜F（b），即f（x）－g（x）＜f（b）－g（b）.

故f（x）+g（b）＜g（x）+f（b）.应选D.

评注：解答过程没有过多考虑f（x）与g（x）在某具体点处的函数值的大小问题，而是从构造差函数入手，并利用差函数的导数研究新函数的单调性，快捷地得到相应的结论.

三、正难则逆

对于某些关于抽象函数的命题，当利用直接法无从下手时，可考虑运用反证法，这样往往可以起到简捷明快、化难为易的解题效果.

例3已知函数f（x）对其定义域内的任意两个实数a、b，当a＜b时，都有f（a）＜f（b），求证：方程f（x）=0至多有一个实根.

分析：直接证明较难把理由说清，但若考虑用反证法，则可以迅速解决问题.

证明：假设方程f（x）=0至少有两个不等的实根x1和x2，不妨设x1＜x2，则f（x1）=0，f（x2）=0，f（x1）=f（x2），这与由题设得到的“f（x1）＜f（x2）”矛盾，故假设不成立，即方程f（x）=0至多有一个实根.

四、适当赋值

“赋值法”是指给变量赋以符合条件的一个或几个值，亦可以是赋以符合条件的一个函数、一个方程、一个不等式、一个几何图形、一个函数图像等，变“抽象”为“具体”，对解决抽象函数问题往往能起到柳暗花明、峰回路转的功效.

例4（2008年陕西高考题）已知f（x）是定义在实数集R上的函数，而且满足f（x+y）=f（x）+f（y）+2xy（x、y∈R），f（1）=2，则f（－3）等于（）.

A.2 B.3 C.6 D.9

解析：令x=－1，y=－2，则f（－3）=f（－1－2）=f（－1）+f（－2）+4，由此可见，需要先求出f（－2）、f（－1）.

令x=y=－1，得f（－2）=f（－1－1）=f（－1）+f（－1）+2；令x=1，y=－1，得f（0）=f（1－1）=f（1）+f（－1）－2=f（－1）；令x=y=0，得f（0）=f（0+0）=f（0）+f（0）+0⇒f（0）=0.逐步向上代入，得f（－3）=6，故应选C.

评注：用“赋值法”探求抽象问题时应注意两个原则：当需要求解抽象函数的具体函数值时，我们应以需要为原则，给变量赋恰当的值；当需要研究抽象函数的性质时，我们可采用消元思想，给变量对称赋值，求出抽象函数的解析式.

五、整体思考

这种策略适合解答两类抽象函数问题：一是已知几个抽象函数的奇偶性，求解由这几个函数构成的更复杂函数的某一函数值，可利用奇偶性整体思考解决；

二是已知一个函数方程求函数解析式，可将函数方程中的自变量x代换成别的自变量（应注意函数的定义域不发生变化），得到一个或几个新的函数方程，然后设法联立原方程，通过整体消元求得函数的解析式.

例5已知f（x）、g（x）为奇函数，F（x）=af（x）+bg（x）+3（a、b为常数），若F（4）=－4，则F（－4）=_______.

分析：由于F（x）的解析式中含有两个参数a、b，但只知F（4）=－4，无法用待定系数法确定a、b的值，因此解析式不确定，可利用奇偶性整体思考解决.

解析：设φ（x）=af（x）+bg（x），则φ（x）=F（x）－3.由题设可知φ（x）为奇函数，则φ（－4）=－φ（4）=－［F（4）－3］=7.又φ（－4）=F（－4）－3，则F（－4）=10.

评注 上述解法的实质是运用整体思想求解，即先化整体为局部，再由各局部的解决使问题获解.

六、以直代曲

在解与抽象函数有关的不等式或其参数范围时，可根据函数图像经过的特殊点或部分图像特征，把函数图像近似处理，采取“以直代曲”的方式，把复杂问题简单化.

例6已知（fx）是R上的减函数，且（fx）的图像过点A（0，3）和点B（3，-1），则不等式＜2的解集为（ ）.

A（.－∞，3）B（.－∞，2）C（.0，3）D（.－1，2）

评注：上述思考问题的方法也经常被用于研究一条曲线的某一小段上任意一点处的切线的斜率的近似值.

七、巧用结论

在平时学习中，留心识记并灵活运用教材上的一些典型结论，往往会给解题带来意想不到的效果.如以下两例就是对教材上这样一个结论的应用：若函数y=（fx）（x∈A，y∈C）有反函数y=f-（1x）（x∈C，y∈A），则：（1）f-［1（fx）］=x（x∈A）；（2）［ff-（1x）］=x（x∈C）.

例7定义在实数集R上的函数f（x）存在反函数，而且对于任意x∈R恒有f（x）+f（-x）=2，则f-1（2008-x）+f-1（x-2006）的值为（ ）.

A.0 B.2 C.3 D.不能确定，与x有关

解析：设f-1（2008-x）=a，f-1（x-2006）=b，由结论（2）得f（a）=2008-x，f（b）=x-2006，则f（a）+f（b）=2，即f（a）=2-f（b）.又f（-b）=2-f（b），则f（a）=f（-b）.又由函数f（x）存在反函数，可知a=-b⇒a+b=0，即f-1（2008-x）+f-1（x-2006）=0，故应选A.

评注：此题设计精致，是一道不折不扣的小综合题，同时紧扣函数存在反函数的条件，源于课本，活而不难，解题的关键在于灵活应用结论（2）引出“f（a）+f（b）=2“这一隐含要素.

八、形数转换

根据题目所给的函数的有关性质和背景，作出函数大致符合条件的一个图像，可化无形为有形，增强解题的直观性.

例8若f（x）为奇函数，且在（-∞，0）上单调递增，又f（-2）=0，则不等式xf（x）＜0的解集为（）.

A.（-2，0）∪（0，2）B.（-∞，-2）∪（0，2）

C.（-∞，-2）∪（2，+∞）D.（-2，0）∪（2，+∞）

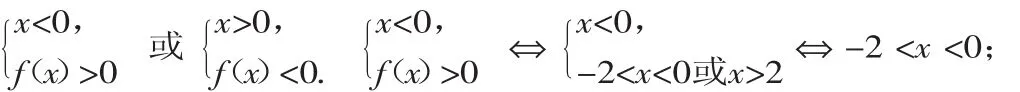
评注：解决类似抽象函数问题，作出与条件大致吻合的草图是解题的关键.

九、换元化归

根据题目结构与求解的问题，将题中的某些代数式替换成所需要的字母，问题转化为关于该字母的代数或几何问题，但要注意新字母的取值范围.

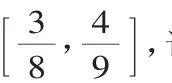
评注：对于抽象函数的值域问题，通过换元变抽象为具体，化归为具体函数的值域问题方可求解，同时要注意新元的取值范围与原字母或代数式的取值范围的区别和联系.

十、两边夹法

两边夹法的原理是：若a≤b，且a≥b，则a=b.此法对解决一些含抽象不等式的求值问题极其有用.

例10设f（x）是定义在R上的函数，若f（0）=2010，对任意x∈R，满足f（x+2）-f（x）≤3·2x，f（x+6）-f（x）≥63·2x，则f（2010）等于（ ）.

A.22008+2007 B.22009+2008 C.22010+2009 D.22011+2010

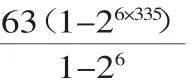
评注：除两边夹法外，联想an-a1=（a2-a1）+（a3-a2）+…+（an-an-1），得等式f（x+6）-f（x）=［f（x+6）-f（x+4）］+［f（x+4）-f（x+2）］+［f（x+2）-f（x）］是解答本题的另一个亮点.

十一、归纳证明

此法适用于在已知解析递推式的前提下求解函数解析式或证明函数的性质.

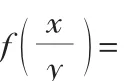
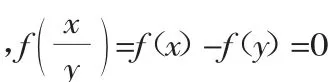
评注：通过若干数据实验，用不完全归纳法作出猜想，再用数学归纳法证明，这是处理抽象函数递推型问题的常用方法.